Метод неопределенных коэффициентов
Метод применим для минимизации функций алгебры логики от любого числа переменных.
Рассмотрим случай трех переменных. Булева функция в ДНФ может быть представлена в виде всевозможных конъюнктивных членов, которые могут входить в ДНФ:
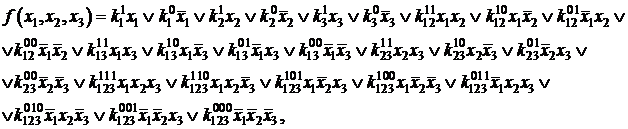
где kО{0,1} ‑ коэффициенты. Метод заключается в подборе коэффициентов таким образом, чтобы получаемая ДНФ была минимальной.
Если теперь задать всевозможные значения переменных от 000 до 111, то получим 2n (23 =8) уравнений для определения коэффициентов k:
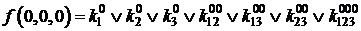 ;
;
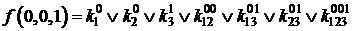 ;
;
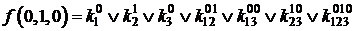 ;
;
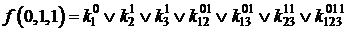 ;
;
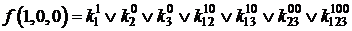 ;
;
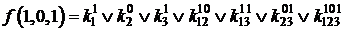 ;
;
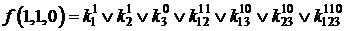 ;
;
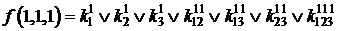 .
.
Рассматривая наборы, на которых функция принимает нулевое значение, определяют коэффициенты, которые равны 0, и вычеркивают их из уравнений, в правой части которых стоит 1. Из оставшихся коэффициентов в каждом уравнении к единице приравнивают по одному коэффициенту, определяющему конъюнкцию наименьшего ранга. Остальные коэффициенты приравнивают к 0. Итак, единичные коэффициенты k определяют соответствующую минимальную форму.
Пример. Минимизировать заданную функцию
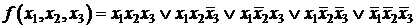 ,
,
если известны значения: 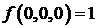 ;
; 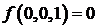 ;
; 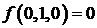 ;
; 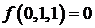 ;
; 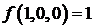 ;
; 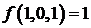 ;
; 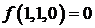 ;
; 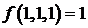 .
.
Решение.
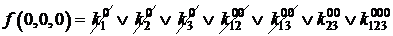 =1;
=1;
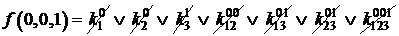 =0;
=0;
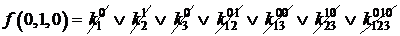 =0;
=0;
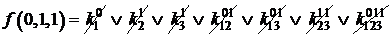 =0;
=0;
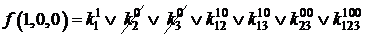 =1;
=1;
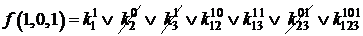 =1;
=1;
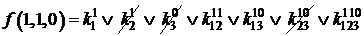 =1;
=1;
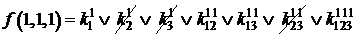 =1.
=1.
После вычеркивания нулевых коэффициентов получим:
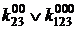 =1;
=1;
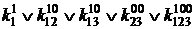 =1;
=1;
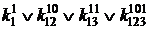 =1;
=1;
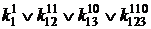 =1;
=1;
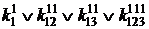 =1.
=1.
Приравняем к единице коэффициент 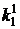 , соответствующий конъюнкции наименьшего ранга и обращающий четыре последних уравнения в 1, а в первом уравнении целесообразно приравнять к 1 коэффициент
, соответствующий конъюнкции наименьшего ранга и обращающий четыре последних уравнения в 1, а в первом уравнении целесообразно приравнять к 1 коэффициент 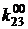 . Остальные коэффициенты приравнивают к 0.
. Остальные коэффициенты приравнивают к 0.
Ответ: вид минимизированной функции 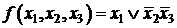 .
.
Следует отметить, что метод неопределенных коэффициентов эффективен, когда число переменных невелико и не превышает 5-6.
Многомерный куб
Рассмотрим графическое представление функции в виде многомерного куба. Каждой вершине n-мерного куба можно поставить в соответствие конституенту единицы.
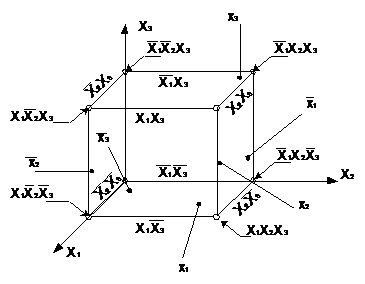
Подмножество отмеченных вершин является отображением на n-мерном кубе булевой функции от n переменных в СДНФ.
Для отображения функции от n переменных, представленной в любой ДНФ, необходимо установить соответствие между ее минитермами и элементами n-мерного куба.
Минитерм (n-1)-го ранга 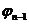 можно рассматривать как результат склеивания двух минитермов n-го ранга, т.е.
можно рассматривать как результат склеивания двух минитермов n-го ранга, т.е.
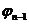 =
= 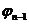
На n-мерном кубе это соответствует замене двух вершин, которые отличаются только значениями координат хi, соединяющих эти вершины ребром (говорят, что ребро покрывает инцидентные ему вершины).
Таким образом, минитермам (n-1)-го порядка соответствуют ребра n-мерного куба.
Аналогично устанавливается соответствие минитермов (n-2)-го порядка граням n-мерного куба, каждая из которых покрывает четыре вершины (и четыре ребра).
Элементы n-мерного куба, характеризующиеся S измерениями, называются S-кубами.
Так вершины являются 0-кубами, ребра 1-кубами, грани 2-кубами и т.д.
Обобщая, можно сказать, что минитерм (n-S) ранга в ДНФ для функции n переменных отображается S-кубом, причем каждый S-куб покрывает все те кубы низшей размерности, которые связаны только с его вершинами.
Пример. На рис. дано отображение 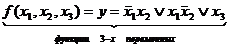

Здесь минитермы 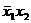 и
и 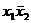 соответствуют 1-кубам (S=3-2=1), а минитерм х3 отображается 2-кубам (S=3-1=2).
соответствуют 1-кубам (S=3-2=1), а минитерм х3 отображается 2-кубам (S=3-1=2).
Итак, любая ДНФ отображается на n-мерном кубе совокупностью S-кубов, которые покрывают все вершины, соответствующие конституентам единицам (0-куба).
Конституенты. Для переменных х1, х2,… хn выражение 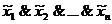 называют конституентой единицы, а
называют конституентой единицы, а 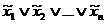 — конституентой нуля (
— конституентой нуля ( 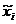 означает либо
означает либо 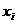 , либо
, либо 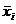 ).
).
Данная конституента единицы (нуля) обращается в единицу (нуль) только при одном соответствующем ей наборе значений переменных, который получается, если все переменные принять равными единице (нулю), а их отрицания — нулю (единице).
Например: конституенте единице 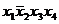 соответствует набор (1011), а конституенте нуля
соответствует набор (1011), а конституенте нуля 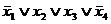 — набор (1001).
— набор (1001).
Так как СД(К)НФ является дизъюнкцией (конъюнкцией) конституент единицы (нуля), то можно утверждать, что представляемая ею булева функция f(x1,x2,…,xn) обращается в единицу (нуль) только при наборах значений переменных x1,x2,…,xn, соответствующих этим копституантам. На остальных наборах эта функция обращается в 0 (единицу).
Справедливо и обратное утверждение, на котором основан способ представления в виде формулы любой булевой функции, заданной таблицей.
Для этого необходимо записать дизъюнкции (конъюнкции) конституент единицы (нуля), соответствующих наборам значений переменных, на которых функция принимает значение, равное единице (нулю).
Например, функции, заданной таблицей
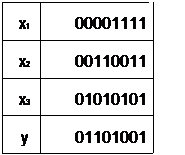
соответствуют
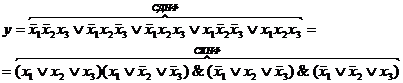
Полученные выражения можно преобразовать к другому виду на основании свойств алгебры логики.
Справедливо и обратное утверждение: если некоторая совокупность S-кубов покрывает множество всех вершин, соответствующих единичным значениям функции, то дизъюнкция соответствующих этим S-кубам минитермов является выражением данной функции в ДНФ.
Говорят, что такая совокупность S-кубов (или соответствующих им минитермов) образует покрытие функции. Стремление к минимальной форме интуитивно понимается как поиск такого покрытия, число S-кубов которого было бы поменьше, а их размерность S — побольше. Покрытие, соответствующее минимальной форме, называют минимальным покрытием.
Например, для функции у= 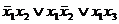 покрытие соответствует неминимальной форме:
покрытие соответствует неминимальной форме:
рис a) у= 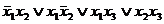 ,
,
а покрытия на рис б) у= 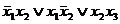 , рис в) у=
, рис в) у= 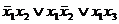 минимальные.
минимальные.
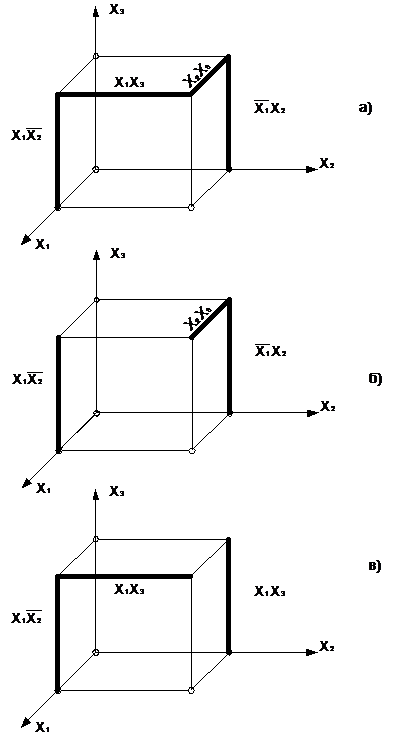
Рис. Покрытие функции у= 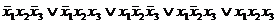 :
:
а) неминимальное; б), в) минимальное.
Отображение функции на n-мерном наглядно и просто при n£3. Четырехмерный куб можно изобразить, как показано на рис., где отображены функции четырех переменных и ее минимальное покрытие, соответствующее выражению у= 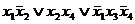
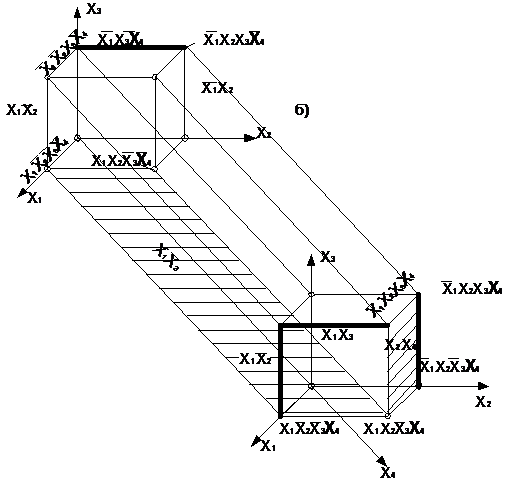
Использование этого метода при n>4 требует настолько сложных построений, что теряет все его преимущества.
Карты Карно
В другом методе графического отображения булевых функций используют карты Карно — специально организованные таблицы соответствия.
Столбцы и строки таблицы соответствуют всевозможным наборам значений не более 2-х переменных, причем эти наборы расположены в таком порядке, что каждый последующий отличается от предыдущего значением только одной из переменных. Благодаря этому и соседние клетки таблицы по горизонтали и вертикали отличаются только одной переменной. Клетки, расположенные по краям таблицы, также считаются соседними и обладают этим свойством.
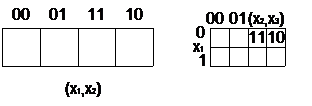
Рис. Карты Карно для 2-х и 3-х переменных.
