Лабораторная работа №6: «Математическое

планирование эксперимента»

1. Теоретическая часть

Целью любого эксперимента является с одной стороны – выявление новых закономерностей, а с другой – формулировка математических моделей, адекватно описывающих изучаемые явления.

При планировании многофакторного эксперимента по классическому плану несколько факторов фиксируются на одном уровне, и только один является переменным. Не всегда корректно допускать возможность стабилизации всех переменных при последовательном выделении каждой из них. В изучаемом процессе (явлении) все факторы действуют одновременно. К тому же, в случае трех- и более факторного эксперимента количество опытов значительно возрастает.

Методы математического планированияпозволяют одновременно изучать влияние нескольких факторов на исследуемый объект. При этом резко сокращается количество опытов, по результатам которых составляется математическая модель процесса.

Преимущества математического планирования:

1. Сокращение объема и удешевление стоимости эксперимента (в 2-10 раз);

2. Создание математической модели процесса или объекта;

3. Оптимизация и контроль за ходом технологических процессов;

4. Подбор многокомпонентных составов новых материалов.

Построение эксперимента отличается большой логикой, рандомизируется постановка опытов, создается возможность проведения регрессионного, корреляционного и дисперсионного анализов.

Активный эксперимент – когда факторам можно произвольно задавать некоторые определенные значения и поддерживать их в течении опыта.

В пассивном эксперименте исследователь не планирует опыты, а лишь регистрирует ход процесса, пытаясь затем установить количественную зависимость между входными и выходными параметрами процесса.

2. Планирование активного эксперимента

· Прежде чем планировать эксперимент, нужно сформулировать цель исследования.

· Выбрать параметр оптимизации, т.е. тот показатель процесса, по которому будет проводиться оптимизация.

· Установить факторы, влияющие на процесс.

В технологических задачах целью исследования при оптимизации процесса чаще всего являются:

Ø Повышение выхода реакции;

Ø Улучшение качества продукта;

Ø Снижение его себестоимости;

Ø Нахождение области реакции с более низкой температурой;

Ø Сокращение времени реакции.

Наиболее широко используются планы экстремального эксперимента.

План экстремального эксперимента.

Основные понятия.

y – функция отклика (параметр оптимизации).

z₁, z₂, z₃…z_n – факторы, влияющие на процесс.

Имеем исследуемую непрерывную функцию

y=f(z₁,z₂,z₃…z_n)

Например, зависимость выхода бензина от температуры( Т°С), давления ( Р МПа) и т.д.

Эту непрерывную функцию можно разложить в ряд (полином) Тейлора:∙

Y = β₀ + β₁Z₁ + β₂Z₂ + … + β_nZ_n + β₁₂Z₁Z₂ + … + β_n-1,nZ_n-1Z_n + β₁₁Z₁² + β₂₂Z₂² + … + β_nnZ_n²

Этот полином аналогичен уравнению регрессии:

y=a₀+∑a_i∙x_i+∑a_ij∙x_ij+∑a_ii∙x_i², (12)

где a₀, a_ij, a_i, a_ii – коэффициенты регрессии, рассчитываются по экспериментальным данным.

x_i – кодированная переменная, введенная в целях упрощения арифметических расчетов.

X_i = (Z_i – Z_0i) / ∆Z_i, (13)

где Z_i – в экстремальном плане имеет два значения (Z_{i max} и Z_{i min})

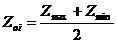, (14)

где Z_oi – средний (нулевой) фактор

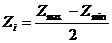, (15)

где ∆Z_i – интервал варьирования фактора.

Эксперимент, при котором реализуются все возможные комбинации факторов на выбранных уровнях, называется полным факторным экспериментом (ПФЭ). Количество опытов при ПФЭ подсчитывается по формуле N=Lⁿ где N – количество опытов, L – количество уровней, n – количество факторов.

Последовательность планирования:

1. Выбирают параметр оптимизации.

2. Выбирают из n действующих факторов наиболее значимые z₁, z₂, z₃…z_n.

3. Устанавливают пределы изменения выбранных факторов z_{i max} и z_{i min}, вычисляют z_{i 0} и ∆z_i, заменяют переменные z_i на кодированные x_i.

4. Определяют комбинации факторов z_i, при которых будет изучаться заданная система. Составляют план-матрицу эксперимента.

5. Разрабатывают методики измерения выбранных факторов, определяют погрешности и число повторений в каждом опыте.

6. Проводят эксперимент, одновременно корректируют его с учетом полученных данных.

7. Определяют уравнение регрессии, проверяют его адекватность, анализируют и делают выводы.

Пример:

Тема: оптимизация процесса изомеризации карбометоксисульфанила.

Цель: изучить влияние условий проведения реакции.

Задачи:

- исследовать влияние температуры;

- исследование влияния времени;

- определить математическую модель..процесса

Исходные данные:

у – выход реакции, %

z₁ – температура, °С

z₂ – время реакции, час

1. Устанавливаем максимальный и минимальный уровни факторов.

z_{1 max} = 175°С; z_{2 max} = 6 ч

z_{1 min} = 165°С; z_{2 min} = 4 ч

z_{1 0}=(175+165)/2=170; ∆z₁ =( 175-165)/2=5

z_{2 0} =( 6+4)/2=5 ∆z₂ = (6-4)/2=1

2. Заменяем факторы кодированными переменными.

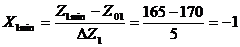
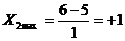
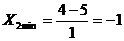
После того, как выбраны уровни факторов и интервалы их варьирования, составляем таблицу, в которой сведены все характеристики плана эксперимента.

Таблица 3.3

Основные характеристики плана эксперимента

Характеристики	Т, °С	Х1	Врем, ч	Х2
Верхний уровень		+1		+1
Нижний уровень		-1		-1
Среднй уровень (нулевой
Интервал варьирования		-		-

3. Составляем план-матрицу эксперимента

При варьировании двух факторов на двух уровнях возможны четыре комбинации. Таким образом, имеем полный факторный эксперимент ПФЭ типа 2². Составляем план-матрицу эксперимента и проводим эксперимент. Результаты заносим в таблицу 3.4.

Таблица 3.4

План-матрица и результаты эксперимента

Номер опыта	Х1	Х2	Z1	Z2	Yэ	Yp	∆Y= (Yp - Yэ)/Yэ,%
Кодированные переменные	Факторы	Выход реакции в эксперименте	Выход реакции расчётный
	-1	-1			50,7	50,7
	+1	-1			66,1	66,1
	-1	+1			55,9	55,9
	+1	+1			84,9	84,9
						64,4	11,8

4. Определяем математическую модель процесса.

Результаты эксперимента, проведённого по типу 2², можно представить уравнением регрессии:

Y = a₀ + a₁X₁ + a₂X₂ + a₁₂X₁X₂ + a₁₁X₁² + a₂₂X₂²

Вначале проверяем возможность линейного полинома:

Y = а₀ + a₁X₁ + а₂Х₂ + а₁₂Х₁Х₂

Для этого необходимо определить коэффициенты регрессии свойствами матрицы планирования:

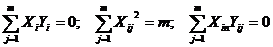
m - число опытов факторного эксперимента;

j - номер опыта;

i,n - номер фактора.

Коэффициенты регрессии можно вычислить по формулам:

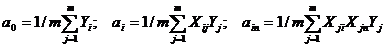
где m– число опытов (m=4)

I, n – номер фактора (1,2)

J – номер опыта

a₀ = 0,25(50,8+66,2+56,0+85,0)=64,4

a₁ = 0,25(-50,8+66,2-56,0+85,0)=11,1

a₂ = 0,25(-50,8-66,2+56,0+85,0)=6,0

a₁₂ = 0,25(50,8-66,2-56,0+85,0)=3,4

5. Записываем уравнение регрессии

y=64,4+11,1 х₁ +6,0 x₂ 3,4 х₁ x₂

Это уравнение показывает, как в среднем меняется y с изменением x.

6. Далее необходимо проверить адекватность линейной модели. Для этого вычисляем y_расч для каждого опыта, подставляя кодированные переменные с их значениями в уравнение:

y₁ =64,4+11,1*(-1)+6,0*(-1)+3,4(-1)(-1) = 50,7

y₂ = 64.4+11.1*(+1)+6.0*(-1)+3.4*(+1)(-1) = 66,1

y₃ = 64.4+11.1*(-1)+6.0*(+1)+3.4*(-1)(+1) = 55,9

y₄ = 64.4+11.1*(+1)+6.0*(+1)+3.4*(+1)(+1) = 84,9

Результат заносим в таблицу (графа y_p).

7. Проводим контрольный эксперимент, чтобы оценить адекватность уравнения линейной модели.

Опыт №5 проводим при нулевых значениях факторов. Результат показал y_э = 73%. Для этого опыта также определяем расчетное значение y_р:

y_р = 64,4+11,1*0+6,0*0+3,4*0=64,4

Условием адекватности уравнения линейной модели является условие разницы между y_р и y_э в опыте при нулевых уровнях менее 25%, т.е.

∆y= .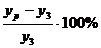

В нашем примере уравнение регрессии оказалось адекватным линейной модели (11,8%).

3. Интерпретация уравнения регрессии

Уравнение можно упростить, т.к. коэффициент a₁₂ малозначим по сравнению с другими (3,4) и им можно пренебречь. Окончательно имеем уравнение:

y=64,4+11,1х₁+6,0х₂

Наибольший коэффициент a₁ =11,1 показывает, что с увеличением температуры выход реакции увеличивается наиболее интенсивно. Значение а₂ примерно в 2 раза меньше а₁. Увеличение времени реакции также положительно сказывается на увеличении выхода реакции, но этот фактор влияет не столь сильно.

Полученный полином можно представить в натуральных значениях факторов, подставив в полученное уравнение вместо кодированных переменных исходные факторы:

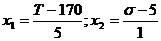
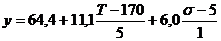
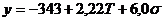
Можно рассчитать выход продукта при различных параметрах процесса.

Если полученное уравнение не соответствует линейной модели, то эксперимент продолжают, представив исследуемую зависимость в виде квадратного полинома:

y = a₀+∑a_i·x_i +∑a_ij·x_ij +∑a_ii·x_i².

В настоящее время разработаны программы, позволяющие реализовать процесс планирования и обработки эксперимента на ЭВМ.

Приложение №1.

t-значения распределения Стьюдента.

Число степеней свободы (N-1)	Доверительные уровни (надежность)
90%	95%	99%
	6,314 2,920 2,353 2,132 2,015 1,943 1,895 1,860 1,833 1,812 1,796 1,782 1,771 1,761 1,753 1,725 1,708 1,697	12,706 4,303 3,182 2,776 2,571 2,447 2,365 2,306 2,262 2,228 2,201 2,170 2,160 2,145 2,131 2,086 2,060 2,042	63,657 9,925 5,841 4,604 4,032 3,707 3,499 3,355 3,250 3,169 3,106 3,055 3,012 2,977 2,947 2,845 2,787 2,750

Приложение №2.

Варианты заданий к лабораторной работе №1.

№ п/п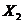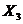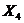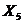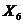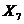
	25,6	25,8	25,4	25,0	25,3	26,8	25,7
	12,5	13,6	12,0	12,6	13,4	11,8	12,7
	10,3	12,0	12,6	9,8	11,4	10,6	10,8
	4,5	4,7	4,4	4,0	5,0	4,3	4,6
	5,6	5,8	5,4	5,0	6,1	5,4	5,9
	3,2	3,4	3,6	3,8	4,0	4,2	3,9
		3,8
	22,5	23,6	22,0	22,6	23,0	21,8	22,4

Приложение №3.

Варианты заданий к лабораторной работе №2.

№ п/п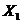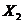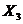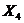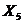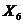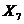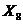
	25,6	25,8	25,4	25,0	25,3	26,8	25,7	27,6
	12,5	13,6	12,0	12,6	13,4	11,8	12,7	14,0
	10,3	12,0	12,6	9,8	11,4	10,6	10,8	8,3
	4,5	4,7	4,4	4,0	5,0	4,3	4,6	5,5
	5,6	5,8	5,4	5,0	6,1	5,4	5,9	6,4
	3,2	3,4	3,6	3,8	4,0	4,2	3,9	4,6
		3,8
	22,5	23,6	22,0	22,6	23,0	21,8	22,4	24,2

Приложение 4

Варианты заданий к лабораторной работе №3.

Подобрать эмпирическую формулу для следующих измерений.

x	y	x	y	x	y	x	y	x	y	x	y	x	y	x	y
	0,31													3,2
	0,44													3,4
	0,51													3,6
	0,54													3,8
	0,59													4,0
	0,63													4,2

Литература

1. Венецкий И.Г.. Теория вероятности и математическая статистика./И.Г.Венецкий, Г.С.Кильдишев. М.: Статистика. - 1975. – 170 с.

2. Налимов В.В., Логическое основание планирования эксперимента/В.В.Налимов, Т.И.Голикова . - М.: Металлургия. - 1981. – 151 с.

3. Герасимов И.Г., Структура научного исследования/ И.Г.Герасимов. - М.: Мысль. - 1985. – 201 с.

4. Закин И.Х., Основы научного исследования/ И.Х.Закин, Н.Р.Рамидов. - Ташкент: ЧКИТУ. - 1981. – 220 с.

5. Зайдель А.Н., . Структура научного исследования/ А.Н.Зайдель, Л.З.Румшин . - М.: Наука. -1971. – 180 с.

6. ГОСТ 24026-80. Исследовательские испытания. Планирование эксперимента. Термины и определения – Введен 06.03.80

Методические указания к лабораторным занятиям по дисциплине «Основы научных исследований» для студентов всех форм обучения специальности 240403 - Химическая технология природных энергоносителей и углеродных материалов

Составители: доцент, к.х.н. Свинтицких Л.Е.

доцент Рычков Д.А.

Подписано к печати Бум. писч. №1

Заказ № Уч. изд. л.

Формат 60/90 1/16 Усл. печ.л.

Отпечатано на RISO GR 3750 Тираж экз.

Издательство «Нефтегазовый университет»

Государственного образовательного учреждения высшего профессионального образования

«Тюменский государственный нефтегазовый университет»

Тюмень,ул. Володарского, 38

Отдел оперативной полиграфии издательства «Нефтегазовый университет»

Тюмень, ул. Киевская, 52