Деки в вычислительных системах

Задачи, требующие структуры дека, встречаются в вычислительной технике и программировании гораздо реже, чем задачи, реализуемые на структуре стека или очереди. Как правило, вся организация дека выполняется программистом без каких-либо специальных средств системной поддержки.

Однако, в качестве примера такой системной поддержки рассмотрим организацию буфера ввода в языке REXX. В обычном режиме буфер ввода связан с клавиатурой и работает как FIFO-очередь. Однако, в REXX имеется возможность назначить в качестве буфера ввода программный буфер и направить в него вывод программ и системных утилит. В распоряжении программиста имеются операции QUEUE - запись строки в конец буфера и PULL - выборка строки из начала буфера. Дополнительная операция PUSH - запись строки в начало буфера - превращает буфер в дек с ограниченным выходом. Такая структура буфера ввода позволяет программировать на REXX весьма гибкую конвейерную обработку с направлением выхода одной программы на вход другой и модификацией перенаправляемого потока.

Сложение многочлена

коэффициент-k; степень-s; первый многочлен-p; второй многочлен-q; |-стрелочка

begin

q1:=q;

p:=p|.next;

q:=q|.next;

while (p|.k<>0) and (p|.s<>0) do

if p|.s<q|.s

then begin

q1:=q;

q:=q|.next;;

end

else

if p|.s>q|.s

then begin

new(q2);

q2|.k:=p|.k;

q2|.s:=p|.s;

q2|.next:=q;

q1|.next:=q2;

q1:=q2;

p:=p|.next;

end

else begin

q|.k:=q|.k+p|.k;

if q|.k=0

then begin

q2:=q;

q1|.next:=q|.next;

q:=q|.next;

dispose(q2);

end

else begin

q1:=q;

q:=q|.next;

end;

p:=p|.next;

q:=q|.next;

end;

end;

49.1 Дерево-рекурсивная, динамическая структура данных.

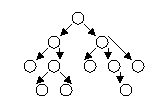Дерево с базовым типом T это либо пустое дерево, любо вершина типа Т с конечным числом связанных с ней деревьев, которые называются поддеревьями.

49.2 Способы изображения деревьев:

Граф – вершины соединяются дугами, согласно их подчинению.

Вложенные множества – любое дерево это множество

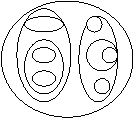
Вложенные скобки - (A, (B, (D), (E, (I), (J))), (C, (K), (M, (P)), (N)))

Отступы

A

B

D

E

I

J

C

K

M

P

N

Корень - самая верхняя вершина дерева.

Корень - вршина не имеющая родителей.

Лист – вершина, не имеющая потомков.

Деревья бывают упорядоченными.

Упорядоченное дерево – дерево, ветви которого упорядоченны по какому-либо признаку

Степень вершины – число поддеревьев, связанных с этой вершиной.(вершины степени 0 носят название концевые, терминальные вершины или листья)

Высота дерева – максимальный путь от корня до листьев дерева

49.3 Способы представления деревьев:

Стандартная форма – в каждой вершине ссылка на всех потомков;

Обратная форма – в каждой вершине ссылка на родительскую(ие) вершины;

Расширенная форма – в каждой вершине хранятся ссылки на потомков и на родителя(ей) этой вершины

49.4 Обход дерева- систематический просмотр всех вершин, при котором каждая вершина встречается один раз.

Прямой

1 попасть в корень

2 пройти левое поддерево

3 пройти правое поддерево

Procedure 01(root:Ttree);

Begin

If root<>nil then begin

Write(root^.inf); 01(root^.left); 01(root^.right);

End;

End.

Обратный

1 пройти левое поддерево

2 попасть в корень

3 пройти правое поддерево

Procedure 01(root:Ttree);

Begin

If root<>nil then begin

01(root^.left); Write(root^.inf); 01(root^.right);

End;

End.

Концевой

1 пройти левое поддерево

2 пройти правое поддерево

3 попасть в корень

Procedure 01(root:Ttree);

Begin

If root<>nil then begin

01(root^.left); 01(root^.right); Write(root^.inf);

End;

End.

50.1 Идеально сбалансированное дерево – дерево, количество вершин в левом и правом поддеревьях которого отличается не более чем на 1.

Построение идеально сбалансированного дерева:

1) расположить 1е число в корне дерева;

2) построить аналитическим методом левое поддерево с кол-ом вершин «n div 2»

3) построить правое поддерево с кол-ом вершин «n - n div 2 – 1»

Function idealtree(n:integer):Ttree;

Var p:Ttree;

Begin

If n=0 then idealtree:=nill;

Else begin

New(p);

Read(p^.inf);

P^.left:=idealtree(n div 2);

P^.right:=idealtree(n - n div 2 - 1);

Idealtree:=p;

End;

End;

50.2

51.1 Алгоритм поиска по дереву с включением:

1.1) 1е значение разместить в корне

1.2) 2е значение сравнивается с тем, что расположено в вершине, если меньше, то вершина левого, если больше, то вершина правого поддерева.

2.1) если новое значение равно, то не выполняется,

2.2) если меньше, то к левому поддереву,

2.3) если больше, то к правому.

Procedure search1(var root:Ttree; x:real);

If root<>nil then begin

New (root);

With root^. Do

Inf:=x;

Left:=nil;

Right:=nil;

End;

Else

If x<root^.inf then search1(root^.left,x)

Else if x>root^.inf then search1(root^.right,x)

Else;

End;

52.1 Ident=record

Name:string;

S:sid

T:ref

Left,right:^Ident;

End;

TIdent=^Ident;

алгоритм идентификации:

1) рассмотреть минимальный блок прикладного вхождения идентификатора, если найдено – процесс завершается,

2) Иначе перейти к блоку, который непосредственно объемлет данный и повторить алгоритм.

Procedure search_ident(x:string;y:sid;z:ref;head:TScope);

Var p:Tscope;

Root:Tident;

Found:Boolean;

Begin

P:=head;

Found:=false;

Repeat

Root :=p^.first_id;

While (root<>nil) and (found=false) do

Begin

If (root^.name=x) and (root^.s:=y) and (root^.t:=z) then

Found:=true;

Else

Begin

If x>root^.name then root:=root^.right

Else if x<root^.name then root:=root^.left

End;

End;

If not found then p:=p^.top_scope;

Until (p=nil) or (found=true)

If not found then error (‘идентификатор не найден’);

End;

Удалить дерево:

procedure delete(var root:tree);

begin

if root<>nil

then begin

delete (root|.left);

delete(root|.right);

dispose(root);

end;

Удалить вершину:

procedure delete_element(var root:tree; x:integer);

var q:tree;

begin

if root<>nil

then

if x<root|.inf

then delete_element(root|.left,x)

else x>root|.inf then delete_element(root|.right,x)

else begin

q:=root;

if q|.right=nil

then root:=q|.left

else if q|.left=nil

then root:=q|.right

else del(q|.left);

dispose(q)

end;

end;

procedure del(var r:tree);

begin

if r|.right<>nil

then del(r|.right)

else begin

q|.inf:=r|.inf;

q:=r;

r:=r|.left;

end;

end;

Сравнение деревьев

function equal(root1,root2:tree):boolean;

begin

if (root1<>nil)and(root2<>nil)

then begin

equal:=(root1|.inf=root2|.inf)

end equal:=(root1|.left=root2|.left)

end equal:=(root1|.right=root2|.right)

else if (root1=nil)and(root2=nil)

then equal:=true

else equal:=false;

end;

Слияние деревьев:

procedure concat(var root1:tree; root2:tree);

begin

if root2<>nil

then begin

search_and_insert(root1,root2|.inf);

concat(root1,root2|.left)

concat(root1,root2|.right)

end;

end;

55.1 АВЛ-дерево — балансированное по высоте двоичное дерево поиска: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.

АВЛ-деревья названы по первым буквам фамилий их изобретателей Адельсона-Вельского и Ландиса.

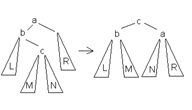
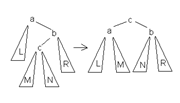
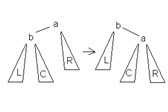
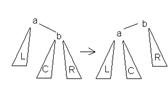
Большое левое вращение(BL) Большое правое вращение(BR) Малое левое вращение(LL) Малое правое вращение(LR)

55.2

Procedure searchavl(var root: avl_tree; x:real;var q:boulean);

Var p2,p1: avl_tree

Begin

If root = nil then

Begin

New(root);

Root^.inf:=x;

Root^.count:=1;

Root^.left:=nil;

Root^.right:=nil;

Root^.bal:=0;

Q:=true;

End;

Else if x<root^.inf then begin

Searchavl (root^.left,x,q);

If q then

Begin

Case root^.bal of

1: begin root^.bal:=0;

Q:=false;

End;

0: begin

Root^.bal:=-1

End;

-1: begin p1:=root^.left;

If p1^.bal=-1 then begin

LL(root,p1);

Root^.bal:=0;

Root:=p1;

End;

Else

Begin

P2:=p1^.left;

LR(root,p1,p2);

If p2^.bal=-1

Then root^.bal:=1;

Else root^.bal:=0;

If p2^.bal=1;

Then p1^.bal:=-1

Else p1^.bal:=0

Root:=p2;

End;

Q:=false;

End;

End;

End;

Else if x>root^.inf then

Begin searchavl(root^.right,x,q);

If q then begin case root^.bal of

-1: begin

root^.bal:=0;

q:=false;

end;

0: root^.bal:=1

1: begin p1:=root^.right;

If p1^.bal=1 then

Begin RR(root;p1);

Root^.bal:=0;

Root:=p1;

End;

Else begin

P2:=p1^.right;

RL(root,p1,p2);

If p2^.bal=1 then

Root^.bal:=1

Else root^.bal:=0

If p2^.bal=-1 then

P1^.bal:=1

Else p1^.bal:=0;

Root:=p2;

End;

Q:=false;

End;

End;

End;

Root^.count:=root^.count+1;

End;

56Сбалансированные деревья(АВЛ-деревья).Дерево называется сбалансированным если высоты его правого и левого деревьев отличны не более чем на 1.

АВЛ-деревья названы по первым буквам фамилий их изобретателей Адельсона-Вельского и Ландиса.

Большое левое вращение(BL) Большое правое вращение(BR) Малое левое вращение(LL) Малое правое вращение(LR)

56.2 procedure deleteavl(var root: avl_tree;x:real;var h:boulean);

var: q:avl_tree;

procedure del (var R:avl_tree; var h:boulean);

begin

if r^.right<>nil then

begin del(r^.right,h)

end;

if h then balanceR(r,h)

else

begin

q^.inf:=r^.inf;

q^.count:=r^.count;

q:=r;

r:=r^.left;

h:=true;

end;

end;

begin

if root=nil then write (‘дерева нет’);

else if x<root^.inf then

begin

deleteavl(root^.left;x;h);

if h then balanceL(root;h);

end;

else if x > root^.inf then

begin

deleteavl(root^.right;x;h);

if h then balanceR(root;h);

end;

else

begin

q:=root;

if q^.right=nil then

begin

root:=q^.left;

h:=true;

end;

else if q^.left=nil then

begin

root:=q^.right;

h:=true;

end;

else begin

del(q^.left;h);

if h then balanceL(root;h);

end;

dispose(q);

end;

end;

procedure balanceL(var root:avl_tree;var h:boulean);

var p1,p2:avl_tree;

begin

case root^.bal of

-1: root^.bal:=0;

0: begin

Root^.bal:=1;

H:=false;

End;

1: begin

P1:=root^.right

If p1^.bal=1 then begin

RR(root;p1);

If p1^.bal=0 then

Root^.bal:=1;

Else root^.bal:=1;

Root:=p1;

End;

Else begin

P2:=p1^.right;

RL(root;p1;p2);

If p2^.bal=1

Then root^.bal:=-1;

Else root^.bal:=0;

If p2^.bal=-1 then

P1^.bal:=-1;

Else p1^.bal:=0;

End;

H:=false;

End;

End;

End;

Type avl_node=record

inf:real;

count:unteger;

left,right:^avl_node;

bal:-1..1;

end;

avl_tree=^avl_tree;

1.)Однократное вращение дерева влево

Procedure LL(var x,y:avl_tree);

Begin

x^.right:=y^.left;

y^.left:=x;

x:=y;

end;

2.)однократный поворот вправо

Procedure RR(var x,y:avl_tree);

Begin

x^.left:=y^.right;

y^.right:=x;

x:=y;

end;

3.)Двойной поворот

Procedure LR(var x,y,z:avl_tree);

Begin

y^.right:=z^.left;

z^.left:=y;

x^.left:=z^.right;

z^.right:=x;

end;

4). Двойной поворот

Procedure RL(var x,y,z:avl_tree);

Begin

y^.left:=z^.right;

z^.right:=y;

x^.right:=z^.right;

z^.right:=x;

end;

58.1 Красно-черное дерево-упорядоченное бинарное дерево в котором выполняются следующие условия:

1) все вершины вакрашены либо в красный, либо в черный цвета,

2) листьями являются значения nil ссылок дерева,

3) Листья всегда черные,

4) Если узел красный, то его непосредственные потомки-черные,

5) Все пути от корня до листьев имеют одинаковую черную величину.

Черная высота - кол-во черных вершин на пути от корня до листьев.

58.2 1) Вставка. Осуществляется изходя из поиска по дереву с включением.

2) Вставляется как «нормальный» лист=>красится в красный цвет.

3) На обратном ходе рекурсии проверяем дерево на предмет красно-черных конфликтов.

Если они найдены, то переупорядочиваем дерево.

Procedure balance(newnote:T_RBTree);

Var parent:T_RBTree;

Begin

Parent:=newnote^.parent;

While(newnote<>root) and (parent^.color=red)do

Begin

If parent^.parent<>nil then begin

If parent=parent^.parent^.left then

Begin

If(parent^.parent^.right<>nil) and(parent^.parent^.right&.color=red)

Then

Begin

parent^.color:=black;

parent^.parent^.color:=red;

parent^.parent^.right^.color:=black;

newnote:=parent^.parent;

end

else

begin

if newnote=parent^.right then

begin

newnote:=parent;

RotateLeft(newnote);

Parent:=newnote^.parent;

End;

Parent^.color:=black;

Parent^.parent.color:=red;

RotateRight(parent^.parent);

End;

End

Else

Begin

If (parent^.parent^.left<>nil) and (parent^.parent^.left^.color:=red) then

Begin

Parent^.color:=black;

Parent^.parent^.left^.color:=black;

Parent^.parent^.color:=red;

Newnote:=parent^.parent;

End

Else

Begin

If newnote = parent^.left then

Begin

Newnote:=parent;

RotateRight(newnote);

Parent:=newnote^.parent;

End;

Parent^.color:=black;

Parent^.parent^.color:=red;

RotateLeft(parent^.parent);

End;

End;

End;

Else

Parent^.parent^.color:=black;

Parent:=newnote^.parent

End;

End;

Procedure RotateRight(a:TRBTree);

Var b:TRBTree;

Begin

B:=a^.left;

A^.left:=b^.right;

If b^.right<>nil then

B^.right^.parent:=a;

If a^.parent<>nil then begin

If a^.parent^.left=a then

A^.parent^.left:= b

Else a^.parent^.right:= b

End;

Else root:= b

B^.parent:=a^.parent;

A^.parent:=b;

B^.right:=a;

End;

Procedure RotateLeft(a:TRBTree);

Var b:TRBTree;

Begin

B:=a^.right;

A^.right:=b^.left;

If b^.left<>nil then

B^.left^.parent:=a;

If a^.parent<>nil then begin

If a^.parent^.right=a then

A^.parent^.right:= b

Else a^.parent^.left:= b

End;

Else root:= b

B^.parent:=a^.parent;

A^.parent:=b;

B^.left:=a;

End;

59.1 Красно-черное дерево-упорядоченное бинарное дерево в котором выполняются следующие условия:

6) все вершины вакрашены либо в красный, либо в черный цвета,

7) листьями являются значения nil ссылок дерева,

8) Листья всегда черные,

9) Если узел красный, то его непосредственные потомки-черные,

10) Все пути от корня до листьев имеют одинаковую черную величину.

Черная высота - кол-во черных вершин на пути от корня до листьев.

59.2 если значение находится на листе, то удаляем это значение с этого листа. Если эл-т не на листовой стороне, то тогда среди значений, находящихся в след.уровне нужно найти то значение, к-ое заменит удаляемое значение (рассматриваем только след.страницы (i) и (i+1)).Если поля переноса в нижестоящей странице получилось, то перерас-пределить значение с i+1на i стран. А если получилось, что здесь n значений и там n значений, то идёт обратная расщеплению ситуация – происходит слияние страниц.

Деревья случайного поиска это сбалансированные деревья, критерий сбалансированности которых, отличается следующим образом:

1. Каждой вершине дерева ставится в соответствие случайное число из диапазона [0;1]

2. Значение случайной величины для каждой вершины дерева должно быть меньше, чем значение случайных величин всех потомков данной вершины.

Вставка в дерево случайного поиска, алгоритм вставки, псевдокод:

1. Вставить вершину в дерево при помощи алгоритма поиска с включением для обычных бинарных деревьев.

2. Для новой вершины сгенерировать случайное число и поставить его в соответствие этой вершины.

3. Выполнить балансировку дерева

Если значение новой случайной величины вершины Х больше значения случайной величины вершины предка Х, или Х является корнем, то завершить балансировку.

Если значение случайной величины вершины Х, меньше значения случайной величины вершины предка Х, то пункт 3.2.1

Если Х является левым потомком, то повернуть на право вершину предок Х. Перейти к пункту 3.1

Если Х является правым потомком, то повернуть на лево вершину предок Х. Перейти к пункту 3.1

Type

RndNode=recor

Inf:Real;

Rnd:Real;

Parend:RndTree; \\ Ссылка на родительскую вершину

Left, right:RndTree;

End;

RndTree=^RndNode;

Var

Root:RndTree; \\ Глобальный указатель на корень дерева

_________

Procedure Insert (Var root:RndTree; parent:RndTree; x:Real);

Begin

If root = nil then begin

New (Root);

Root^.Inf:=x;

Root^.Rud:=Random;

Root^.Parent:=parent;

Root^.Left:=nil;

Root^.Right:=nil;

Balanse (root); end;

Else if x<root^.inf then Insert (root^.Left, root, x)

Else if x<root^.inf then Insert (root^.Right, root, x)

Else write (‘Такая вершина уже есть’);

End;

Procedure Balanse (x:RndTree);

Begin

While (x<>root) and (x^.rnd<x^.parent.rnd) do

Begin

If x=x^.parent^.Left then

Right (x^.parent);

Else Left (x^.parent);

End;

End;

Procedure RotateRight(a:TRBTree);

Var b:TRBTree;

Begin

B:=a^.left;

A^.left:=b^.right;

If b^.right<>nil then

B^.right^.parent:=a;

If a^.parent<>nil then begin

If a^.parent^.left=a then

A^.parent^.left:= b

Else a^.parent^.right:= b

End;

Else root:= b

B^.parent:=a^.parent;

A^.parent:=b;

B^.right:=a;

End;

Procedure RotateLeft(a:TRBTree);

Var b:TRBTree;

Begin

B:=a^.right;

A^.right:=b^.left;

If b^.left<>nil then

B^.left^.parent:=a;

If a^.parent<>nil then begin

If a^.parent^.right=a then

A^.parent^.right:= b

Else a^.parent^.left:= b

End;

Else root:= b

B^.parent:=a^.parent;

A^.parent:=b;

B^.left:=a;

End;

Деревья случайного поиска это сбалансированные деревья, критерий сбалансированности которых, отличается следующим образом:

1. Каждой вершине дерева ставится в соответствие случайное число из диапазона [0;1]

2. Значение случайной величины для каждой вершины дерева должно быть меньше, чем значение случайных величин всех потомков данной вершины.

Алгоритм:

1. Значение случайной величины удаляемой вершины, сделать больше чем единица (Дерево сразу станет не сбалансированным), после балансировки эта вершина станет листом.

2. Выполнить балансировку дерево.

Если удаляемая вершина имеет левого потомка, то выполнить балансировку для левого потомка удаляемой вершины. Перейти к пункту 2.

Если удаляемая вершина имеет правого потомка, то выполнить балансировку для правого потомка удаляемой вершины. Перейти к пункту 2.

Если удаляемая вершина не имеет потомков, то перейти к пункту 3.

3. Удалить вершинную

Type

RndNode=recor

Inf:Real;

Rnd:Real;

Parend:RndTree; \\ Ссылка на родительскую вершину

Left, right:RndTree;

End;

RndTree=^RndNode;

Var

Root:RndTree; \\ Глобальный указатель на корень дерева

Procedure Delete (Var x: RndTree);

Begin

X^.Rnd:=2;

While (x^.left<>nil) or (x^.ridht<>nil) do

Begin

If x^.Left <> nil then

Balanse (x^.left) else

Balanse (x^.Right)

End;

If x^.parent<>nil then begin

If x^.parent^.left=x

Then x^.parent^.Left:=nil

Else x^.parent.right:=nil;

End;

Dispose (x);

End.

62.1 B-дерево-сильно ветвящееся дерево удовлетворяющее перечиленным критериям сбалансированности.

Критерии сбалансированности сильно ветвящихся деревьев:

· Каждая вершина дерева должна иметь не более чем 2*n элементов.

· Каждая вершина за исключением корня дерева, должна иметь не меньше чем N элементов, корень может иметь меньше чем N элементов.

· Каждая вершина дерева является либо листом, либо содержит m+1 потомков, где m это количество элементов на данной вершине. Для любой вершины кроме корня n=<m=<2n, для корня – 1=<m=<2n

· Все листы дерева находятся на одном уровне

program B_Tree; //Реализация B-деревьев

const N=2;

type

TItem=Record

Inf:Real;

P:TBTree;

count:Integer;

end;

TPage=Record

p0:TBTree;

A:array[1..2*N] of TItem;

m:1..2*N;

end;

TBTree=^TPage;

var root: TBTree;

Число n – глубина В дерева.

Пример В дерева 2го порядка

62.2

//поиск места для вставки

procedure search_insert(var root:TBTree; x:real; q:boolean; var new_item:TItem);

var l, r, k:integer;

item:TItem;

begin

if root=nil then

begin

new_item.inf:=x;

new_item.count:=1;

new_item.p:=nil;

q:=true;

end;

else

begin

l:=1;

r:=root^.m;

while l<r do

begin

k:=(L+r) div 2;

if x>root^.A[k].inf then l:=k+1

else if x<root^.A[k].inf then r:=k-1

else l:=r;

end;

if x=root^.A[k].inf then

begin

inc(root^.A[k].count,1);

q:=false;

end;

else

begin

if (root^.m mod 2) = 1 then r:=r-1;

if r=0 then next_page:=root^.p0

else next_page:=root^.A[r].p;

search_insert(next_page,x,q,item);

if q=true then insert(root,item,q,new_item);

end;

end;

end;

//вставка

procedure insert(var root:TBTree; item:TItem; var q:boolean; var new_item:TItem; r:Integer)

var i:integer;

new_apge:TBtree;

begin

if root^.m<2*N then

begin

for i:=root^.m downto r+1 do root^.A[i+1].:=root^.A[i];

root^.A[r+1].:=item;

q:=false;

end

else

begin

new(new_page);

if r<=N then

begin

if r=N then new_item:=item

else

begin

new_item:=root^.A[N];

for i:=N-1 downto r+1 do root^.A[i+1]:root^.A[i];

root^.A[i+1]:=item;

end;

for i:=N+1 to 2*N do new_page^.A[i-N]:=root^.A[i];

end;

else

begin

new_item:=root^.A[N+1];

for i:=n+2 to r do new_page^.A[i-(N+1)]:=root^.A[i];

new_page^.A[r-N]:=item;

for i:=r+1 to 2*N do new_page^.A[i-N]:=root^.A[i];

end;

root^.m:=N;

new_page^.m:=N;

new_page^.p0:=new_item.p;

new_item.p:=new_page

end;

end;

63.1

B-дерево-сильно ветвящееся дерево удовлетворяющее перечиленным критериям сбалансированности.

Критерии сбалансированности сильно ветвящихся деревьев:

· Каждая вершина дерева должна иметь не более чем 2*n элементов.

· Каждая вершина за исключением корня дерева, должна иметь не меньше чем N элементов, корень может иметь меньше чем N элементов.

· Каждая вершина дерева является либо листом, либо содержит m+1 потомков, где m это количество элементов на данной вершине. Для любой вершины кроме корня n=<m=<2n, для корня – 1=<m=<2n

· Все листы дерева находятся на одном уровне

program B_Tree; //Реализация B-деревьев

const N=2;

type

TItem=Record

Inf:Real;

P:TBTree;

count:Integer;

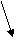
end;

TPage=Record

p0:TBTree;

A:array[1..2*N] of TItem;

m:1..2*N;

end;

TBTree=^TPage;

var root: TBTree;

Число n – глубина В дерева.

Пример В дерева 2го порядка

63.2

//Удаление

procedure delete(var root:TBTree; x:Real; var q:Boolean;)

var i,l,r,k:integer;

newxt_page:TBTree;

begin

if root=nil then write('Element otsutstvuet')

else

begin

l:=1;

r:=root^.m;

while l<r do

begin

k:=(l+r) div 2;

if x>root^.A[k].inf then l:=k+1;

else if x<root^.A[k].inf then r:=k-1

else l:=r;

end;

if (root^.m mod 2) = 1 then r:=r-1;

if x=root^.A[k].inf then

begin

if root^.A[k].p=nil then

begin

for i:=k to 2*n-1 do root^.A[i]:=root^.A[i+1];

Dec(root^.m);

q:=root^.m<N;

end

else

begin

if k=1 then new_page:=root^.p0 else new_page:=root^.A[k-1].p;

Del(root,new_page,q,k);

if q=true then fix(???)

end;

end;

else

begin

if r=0 then new_page:=root^.p0

else new_page:=root^.A[r].p;

delete(new_page,x,q);

if q=true then fix(???);

end;

end;

end;

// Вспомогательная функция

procedure del(var root:TBTree; next_page:TBTree; var q:boolean; k:integer);

begin

if next_page^.A[next_page^.m].p<>nil then

begin

del(root, next_page^.A[next_page^.m].p,q);

if q then fix(???);

end

else

begin

next_page^.A[next_page^.m].p:=root^.A[k].p;

root^.A[k]:=next_page^.A[next_page^.m];

Dec(next_page^.m);

q:=next_page^.m<N;

end;

end;