Способы представления дискретных систем

Автоматического управления

Цель работы

1. Определение дискретных моделей систем автоматического управления по заданным разностным уравнениям или дискретным передаточным функциям.

2. Реализация дискретных моделей на ЭВМ с использованием пакета Matlab.

3. Определение структурных схем дискретных систем, фазовые координаты которых соответствуют реальным физическим переменным.

4. Определение матрицы состояния А, матрицы управления В, матрицы наблюдения С дискретных систем, фазовые координаты которых соответствуют реальным физическим переменным.

5. Исследование структурных схем в пакете MatLab.

Теоретическое обоснование

Процессы в дискретных системах описываются разностными уравнениями

y(kT_П) + a₁y(k – 1)T_П +…+ a_ny(k – n)T_П =

= b₀x(kT_П) + b₁x(k – 1)T_П +…+ b_mx(k – m)T_П.

T_П – интервал отсчета, которых используется при замене непрерывного дифференциального уравнения разностным, а при часто повторяющихся преобразованиях опускается.

y(k) + a₁y(k – 1) +…+ a_ny(k – n) = b₀x(k) + b₁x(k – 1) +…+ b_mx(k – m). (11.1)

Дискретная передаточная функция

y(z) + a₁z^-1y(z) +…+ a_nz^-ny(z) = b₀x(z) + b₁z^-1x(z) +…+ b_mz^-mx(z). (11.2)

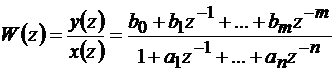. (11.3)

Для дискретных систем в схемах с переменными состояния используется регистр сдвига (рис. 11.1а), который заменяет интегратор непрерывных систем. Через каждый интервал дискретности в момент времени t = kT_П в регистр сдвига записывается новое число x(k), а число x(k-1), которое ранее хранилось в регистре, выводится из него. Изображение такого элемента памяти представлено на рис. 11.1б.

Комбинация из блоков задержки, блоков умножения на константу и сумматоров позволяет построить дискретную модель системы, описываемую дискретными передаточными функциями или разностными уравнениями.

a) б)

Рис. 11.1. Блоки задержки, используемые для моделирования дискретных систем

Выражение (11.1) можно представить относительно y(k)

y(k) = b₀x(k) + b₁x(k – 1) +…+ b_mx(k – m) – a₁y(k – 1) –…– a_ny(k – n). (11.4)

По выражению (11.4) реализована структурная схема, представленная на рис. 11.2. Она носит название прямой формы 1. В ней для образования цепей, соответствующих левой и правой частям уравнения (11.1), используются раздельные элементы задержки. Эта структура проста и непосредственно связана с z-преобразованиями. Но если полюсы передаточной функции (11.3) расположены близко друг от друга или от единичной окружности, то погрешности коэффициентов значительно влияют на результаты преобразования. По этой причине форму 1 стараются не применять.

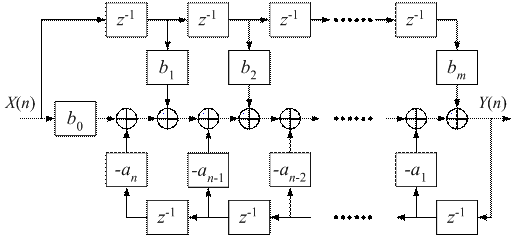
Рис. 11.2. Структурная схема по прямой форме 1

Структурные схемы дискретных систем могут быть составлены по разностным уравнениям или по дискретным передаточным функциям тремя различными способами:

- прямого программирования;

- параллельного программирования;

- последовательного программирования.

Полученные таким путем структурные схемы хотя и позволяют определять матрицы А, В, С и D, но ни одна из промежуточных фазовых координат дискретной системы не соответствует физическим величинам реальной (аналоговой) системы регулирования.

Рассмотрим метод составления структурных схем, основанный на замене оператора непрерывного интегрирования оператором численного интегрирования. Применяются несколько операторов численного интегрирования.

Метод прямоугольников или прямой метод Эйлера

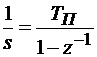, (11.5)

метод прямоугольников или обратный метод Эйлера

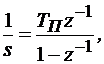(11.6)

метод трапеций

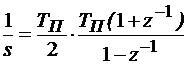. (11.7)

Используя, вышеприведенные операторы, можно перейти от структурной схемы непрерывной системы к структурной схеме дискретной системы. Для того, что бы фазовые координаты дискретных систем отображали физические величины реальной (аналоговой) системы, непрерывные передаточные функции должны быть представлены детализированными структурными схемами (ДСС). Под ДСС понимают структуру состоящую, для линейных систем, из усилительных и интегрирующих звеньев.

Описание работы

Рассмотрим метод прямого программирования. Исходными данными являются непрерывная передаточная функция

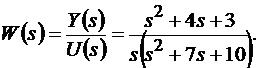(11.8)

Задавая интервал дискретности T_П = 0,2; T_П = 0,1 и T_П = 0,02, с помощью программы MatLab получим z-передаточные функции системы.

h1=tf([1,4,3],[1,7,10,0]) %Исходные данные

t1=0.2 %интервал дискретности

hd1=c2d(h1,t1) %z-передаточная функция при Тп=0.2

t2=0.1 %интервал дискретности

hd2=c2d(h1,t2) %z-передаточная функция при Тп=0.1

t3=0.02 %интервал дискретности

hd3=c2d(h1,t3) %z-передаточная функция при Тп=0.02

Результаты выполнения программы представлены следующими выражениями

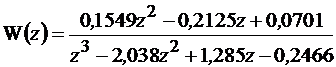при Т_П = t₁, (11.9)

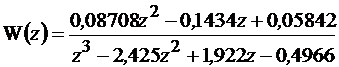при Т_П = t₂, (11.10)

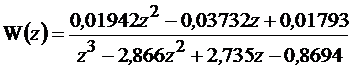при Т_П = t₃, (11.11)

Для реализации схем моделирования следует z-передаточные функции системы записать в форме фильтра (filt) по убывающим степеням z .

Из представленных z-передаточных функций будет реализована структурная схема по выражению (11.9), имеющая, по сравнению с выражениями (11.10) и (11.11), меньшую погрешность

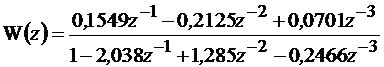(11.12)

По выражению (11.12) составлена структурная схема для моделирования дискретной системы (рис.11.3).

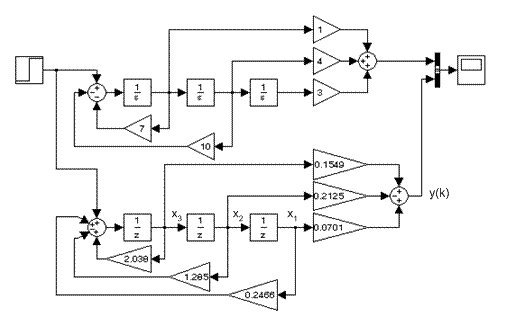
Рис. 11.3. Моделирование дискретных систем методом прямого программирования (mod11_01)

Как видно из выражения (11.12) после первого блока задержки формируются два сигнала: один с коэффициентом 0,1549 идет на выход системы, а второй с коэффициентом –2,038 образует петлю обратной связи. По аналогичному алгоритму формируется сигнал на выходе второго и третьего блоков задержки.

Погрешности при переходе от аналоговой системы к дискретной зависят от интервала дискретности и с увеличением времени возрастают. Например, из трех передаточных функций, определенных выражениями (11.9), (11.10) и (11.11), наименьшей ошибкой характеризуется выражение (11.9).

Матрицы коэффициентов А и Сдискретной системы получим из схем моделирования (рис. 11.3), приняв выход каждого элемента задержки за переменную состояния, обозначив их через x₁, x₂, x₃. Тогда входы элементов задержки будут равны x₁(k + 1), x₂(k + 1), x₃(k + 1), а уравнения состояния запишутся в виде

x₁(k + 1) = x₂(k),

x₂(k + 1) = x₃(k),

x₃(k + 1) = 0,2466x₁(k) – 1,285x₂(k) + 2,038x₃(k) + u(k), (11.13)

y(k) = 0,0701x₁(k) – 0,2125x₂(k) + 0,1549x₃(k).

Эти уравнения можно представить в векторно-матричной форме

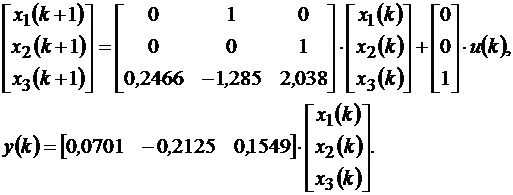(11.14)

Используя стандартный вид, систему уравнений (11.14) можно записать

X(k + 1) = AX(k) + Bu(k),

Y(k) = CX(k).

Структурную схему дискретной системы получают с помощью метода параллельного программирования. Для этого передаточную функцию непрерывной системы (11.8) представляют в виде суммы элементарных дробей

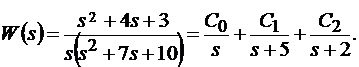
Определяют коэффициенты С₀, С₁, С₂ (лабораторная работа №3). Для каждой элементарной дроби определяем z-преобразование.

h1=tf(3/10,[1,0]) %Исходные данные

h2=tf(8/15,[1,5]) %Исходные данные

h3=tf(1/6,[1,2]) %Исходные данные

t1=0.02

hd1=c2d(h1,t1) %Определение z-передаточных функций

hd2=c2d(h2,t1) %Определение z-передаточных функций

hd3=c2d(h3,t1) %Определение z-передаточных функций.

По результатам выполнения программы получены z-передаточные функции элементарных дробей и составлена структурная схема дискретной системы методом параллельного программирования (рис. 11.4).

Как видно из рис. 11.4 структура дискретной системы по форме совпадает со структурой непрерывной системы, полученной методом параллельного программирования. Для перехода от непрерывной системы к дискретной следует каждому непрерывному каналу поставить в соответствие дискретный канал.

Моделирование дискретной системы методом параллельного программирования характеризуется минимальными ошибками. Для модели, полученной методом параллельного программирования, матрицы коэффициентов А и Стакже могут быть определены из схемы моделирования (рис. 11.4). Приняв выход каждого элемента задержки за переменную состояния, получим уравнения состояния

x₁(k + 1) = x₁(k) + u(k),

x₂(k + 1) = 0,9048x₂(k) + u(k),

x₃(k + 1) = 0,9608x₃(k) + u(k), (11.15)

y(k) = 0,006x₁(k) + 0,01015x₂(k) + 0,003268x₃(k).

Эти уравнения можно представить в векторно-матричной форме

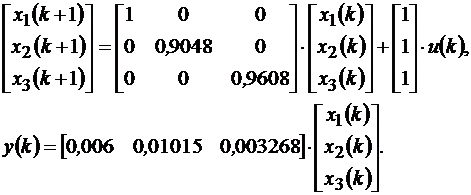(11.16)

При стандартной форме записи система уравнений (11.16) принимает компактный вид

X(k + 1) = AX(k) + Bu(k),

Y(k) = CX(k). (11.17)

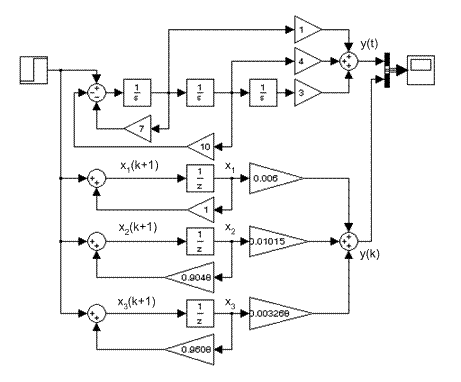
Рис. 11.4. Моделирование дискретных систем

методом параллельного программирования (mod11_2)

При составлении структурной схемы системы методом последовательного программирования передаточную функцию непрерывной системы (11.8) можно представить в виде произведения элементарных блоков

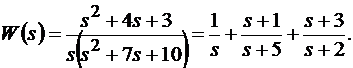
Для каждого элементарного блока следует составить дискретную схему.

h1=tf(1,[1,0])

h2=tf([1,1],[1,5])

h3=tf([1,3],[1,2])

t1=0.02

hd1=c2d(h1,t1)

hd2=c2d(h2,t1)

hd3=c2d(h3,t1).

По результатам выполнения программы получены z-передаточные функции отдельных блоков и составлена структурная схема дискретной системы методом последовательного программирования (рис. 11.5). Совпадения результатов моделирования дискретной системы с непрерывной свидетельствует о правильности методики определения дискретной модели методом последовательного программирования.

Коэффициенты матриц А и С системы, полученной методом последовательно программирования получают из схем моделирования (рис. 11.5).

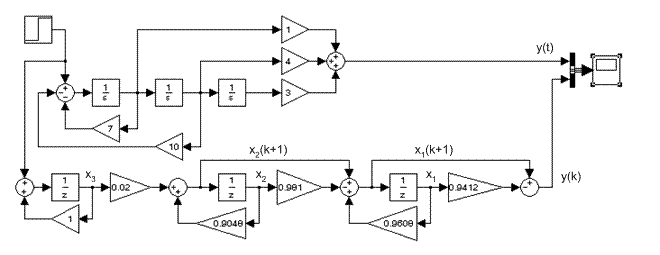
Рис. 11.5. Моделирование дискретных систем

методом последовательного программирования (mod11_3)

x₁(k + 1) = 0,9608x₁(k) + (0,9048 – 0,981)x₂(k) + 0,02x₃(k),

x₂(k + 1) = 0,9048x₂(k) + 0,02x₃(k),

x₃(k + 1) = x₃(k) + u(k), (11.18)

y(k) = (0,9608 – 0,9412)x₁(k) + (0,9048 – 0,981)x₂(k) + 0,02x₃(k).

В стандартной форме записи получим матричную систему уравнений

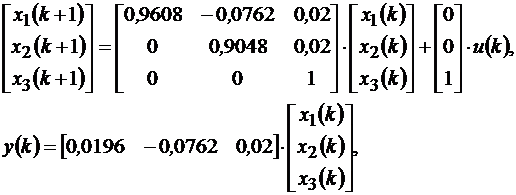(11.19)

из которой определяются матрицы коэффициентов А и С.

Детализированная структурная схема, представленная на рис. 11.6.

Для создания искомой дискретной модели непрерывную передаточную функцию второго примера следует сначала представить детализированной структурной схемой, а затем в этой схеме оператор непрерывного интегрирования заменятся оператором численного интегрирования. В приведенном примере используется три оператора численного интегрирования.

На рис. 11.7 представлен пример системы с передаточной функцией

.

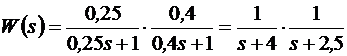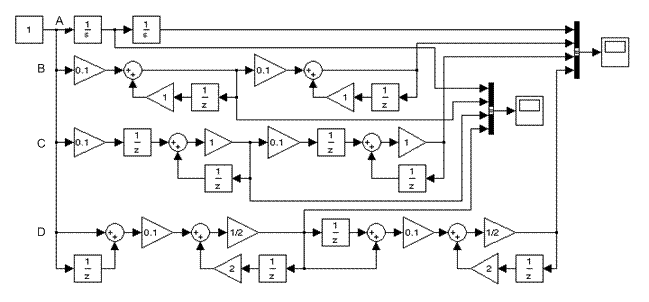
Рис. 11.6. Детализированная структурная схема (А – непрерывная система, В – дискретная

система, аппроксимируемая выражением (9.5), С – дискретная система, аппроксимируемая

выражением (9.6), D – дискретная система, аппроксимируемая выражением (9.7)) mod11_4

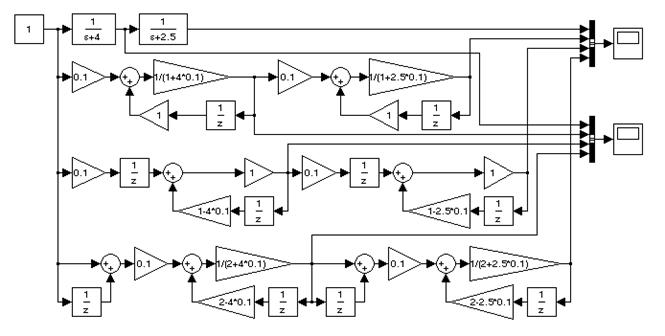
Рис. 11.7. Детализированная структурная схема mod11_5

Задание

1. Для своего варианта по передаточной функции непрерывной системы (табл. 1) определить дискретную передаточную функцию и составить схему моделирования методом прямого программирования.

2. Представить передаточную функцию непрерывной системы в виде суммы элементарных дробей, для каждой элементарной дроби определить дискретную передаточную функцию и методом параллельного программирования составить схему моделирования.

3. Представить передаточную функцию непрерывной системы в виде произведения элементарных дробей, для каждой элементарной дроби определить дискретную передаточную функцию и методом последовательного программирования составить схему моделирования.

4. Определить матрицы А и Сдля структурной схемы, составленной методом прямого программирования.

5. Определить матрицы А и Сдля структурной схемы, составленной методом параллельного программирования.

6. Определить матрицы А и Сдля структурной схемы, составленной методом последовательного программирования.

7. Сравнить ошибки, возникающие при замене непрерывной системы дискретной с различными методами программирования и сделать выводы.

8. По заданной передаточной функции (табл. 2) определить детализированные структурные схемы дискретных систем, используя три метода численного интегрирования.

9. Проверить совпадение переходных процессов по всем координатам и правильность выполнения расчетов.

Содержание отчета

1. Структурные схемы исследуемой системы, полученные методом прямого программирования, методом параллельного программирования и методом последовательного программирования.

2. Расчетные значения дискретных передаточных функций, используемых в методах прямого программирования, параллельного программирования и методе последовательного программирования.

3. Результаты моделирования.

4. Детализированная структурная схема непрерывной системы.

5. Структурные схемы дискретных систем, определенные из детализированной структурной схемы непрерывной системы путем замены оператора непрерывного интегрирования оператором численного интегрирования.

Контрольные вопросы

1. Обоснуйте методику определения структурной схемы дискретной системы методом прямого программирования.

2. Обоснуйте методику определения структурной схемы дискретной системы методом параллельного программирования.

3. Обоснуйте методику определения структурной схемы дискретной системы методом последовательного программирования.

4. Дайте сравнительную характеристику трех методов программирования.

5. Какие команды используются в MatLab при определении z-передаточ-ной функции.

6. Как по структурным схемам непрерывных систем определить матрицы состояния, управления и наблюдения системы.

7. Как по структурным схемам дискретных систем определить матрицы состояния, управления и наблюдения системы.

8. Какие методы численного интегрирования используются при выполнении лабораторной работы.

Лабораторная работа № 12