Моделирование систем автоматического управления

Методом вариации постоянных

Цель работы

1. Аналитическое вычисление фундаментальных матриц при моделировании системы методами прямого, параллельного и последовательного программирования.

2. Решение дифференциальных уравнений методом вариации постоянных.

Теоретическое обоснование

Лабораторная работа выполняется на основе моделей и индивидуального задания лабораторной работы №3.

Непрерывная линейная система также может быть описана дифференциальным векторно-матричным уравнением

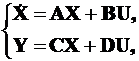(4.1)

где А – матрица коэффициентов состояний размером k´k; В – матрица коэффициентов управления размером k´n; С – матрица коэффициентов наблюдения размером m´k и D – матрица коэффициентов выхода размером m´n; X – вектор состояния (матрица-столбец размером k´l); U – вектор управления (матрица-столбец размером n´l); Y – вектор наблюдения (матрица-столбец размером m´l).

Решение уравнения (4.1) можно выразить через фундаментальные матрицы, определенные несколькими методами.

Первый метод основан на взятии конечного числа элементов разложения

,

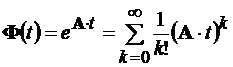где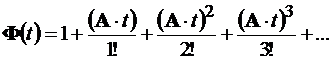

Второй способ основан на аналитическом вычислении матрицы Ф(t).

Преобразование Лапласа векторного дифференциального уравнения 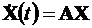дает sX(s) − X(0) =AX(s). Откуда X(s) [Is − A] = X(0) или X(s) = [Is –A]^-1X(0), где I – единичная матрица.

При применении к обеим частям последнего уравнения обратного преобразования Лапласа X(t) = L^-1{[Is − A]^-1}X(0).

Выражение L^-1{[Is − A]^-1} = e^At = Ф(t) определяет фундаментальную матрицу системы.

Множество решений однородного векторно-матричного дифференциального уравнения 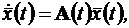где каждому начальному условию 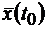соответствует только одно решение дифференциального уравнения, образует N-мерное векторное пространство. Среди множества решений всегда может быть выбрано n линейно независимых. Матрица X(t)_[n´n], столбцами которой являются n линейно независимых решений системы, называется фундаментальной матрицей этой системы дифференциальных уравнений.

Общее решение матричного дифференциального уравнения для известной фундаментальной матрицы Ф(t) определяется формулой Коши (формулой вариации постоянных)

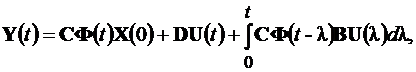(4.2)

где l – собственные значения матрицы Ф.

Описание работы

Рассмотрим систему с передаточной функцией 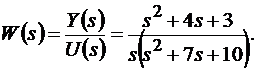(4.3)

(4.3)

Метод прямого программирования

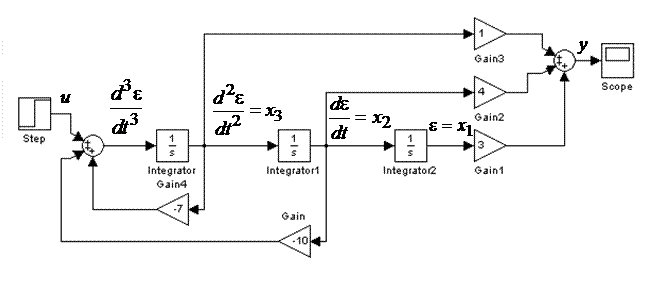
Рис. 4.1. Схема моделирования системы методом прямого программирования

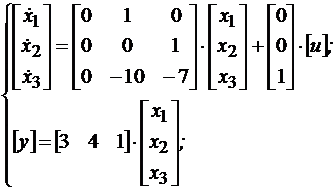(4.4)

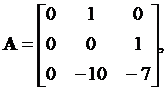
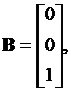C = [3 4 1], D = 0.

Аналитическое вычисление фундаментальной матрицы заключается в определении матрицы состояния A, разности [Is − A], нахождении обратной матрицы и применении обратного преобразования Лапласа к каждому элементу обратной матрицы.

В пакете MatLab эти операции выполняются следующим образом.

A=[0,1,0;0,0,1;0,-10,-7] %Матрица состояния А

syms s %Символьная переменная

Is=[s,0,0;0,s,0;0,0,s] %Единичная матрица

F=inv([Is]-[A]) %Обратная матрица в частотной области

F1=ilaplace(F) %Обратная матрица во временной области.

В результате выполнения программы получают фундаментальную матрицу в частотной области

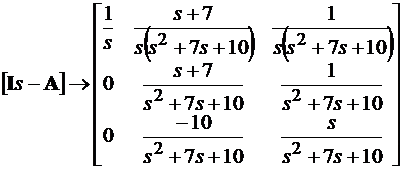(4.5)

и во временной области

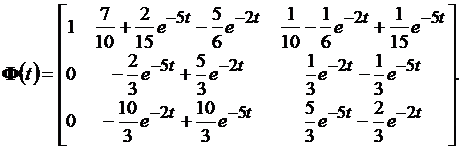(4.6)

Выражение (4.6) получено из (4.5) с помощью обратного преобразования Лапласа применительно к каждому элементу матрицы. В случае нулевых начальных условий X(0) = 0 и нулевой матрицы выхода системы D= 0 первое и второе слагаемое формулы Коши (4.2) равны нулю, откуда

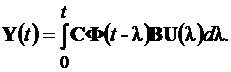(4.7)

Фундаментальная матрица в символьной форме выглядит как

.

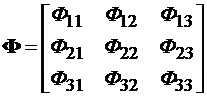Для определения подынтегрального выражения (4.7) вычисляют:

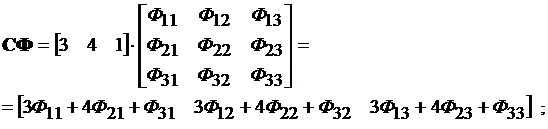
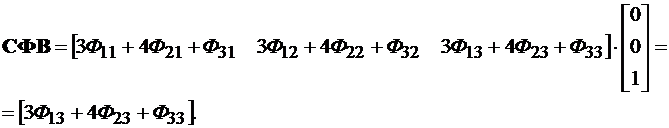СФВU = [3Ф₁₃ + 4Ф₂₃ + Ф₃₃]×[1] = [3Ф₁₃ + 4Ф₂₃ + Ф₃₃] =

= .

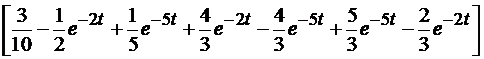Выходную величину системы определяют из выражения (4.7):

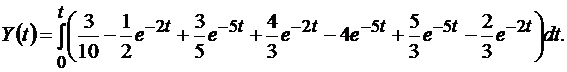
Решение матричного интегрального уравнения

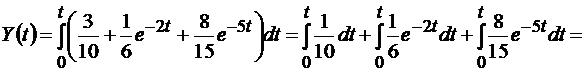
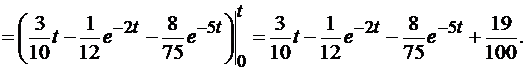
График переходной функции (рис. 4.2) определяют следующим образом

t=0:0.01:1;

y=(3/10)*t-(1/12)*exp(-2*t)-(8/75)*exp(-5*t)+(19/100);

Plot(t,y).

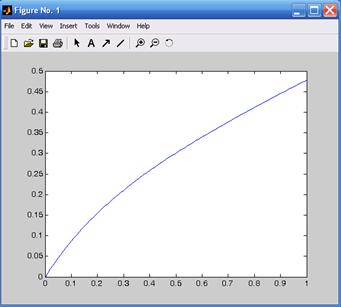
Рис. 4.2. Переходная функция модели, определенная методом прямого программирования

Метод параллельного программирования

При разложении передаточной функции (4.3) методом Хевисайда:

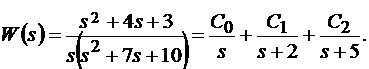(4.8)

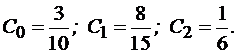(4.9)

С учетом выражения (4.8) получена схема моделирования (рис. 4.3).

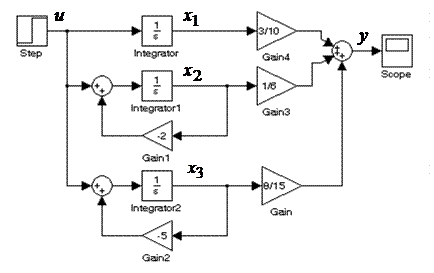
Рис. 4.3. Схема моделирования системы методом параллельного программирования

(4.10)

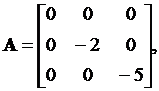
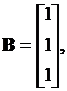
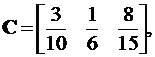D = 0.

Матрица A при параллельном программировании имеет диагональный вид, что достигается выбором базиса, при котором фазовые координаты не влияют друг на друга.

Определяют фундаментальную матрицу Ф(t):

A=[0,0,0;0,-2,0;0,0,-5] %Матрица состояния

syms s %Символьная переменная

Is=[s,0,0;0,s,0;0,0,s] %Единичная матрица

F=inv([Is]-[A]) %Обратная матрица в частотной области

F1=ilaplace(F) %Обратная матрица во временной области.

Фундаментальная матрица в частотной области

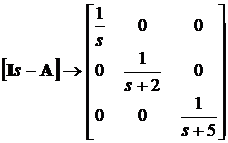
и во временной области

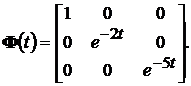
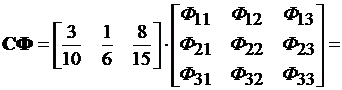
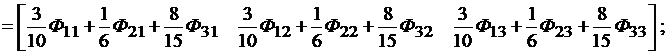
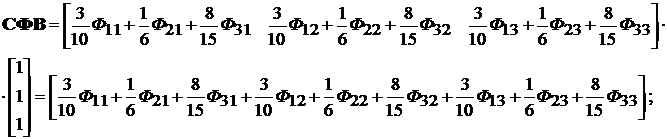
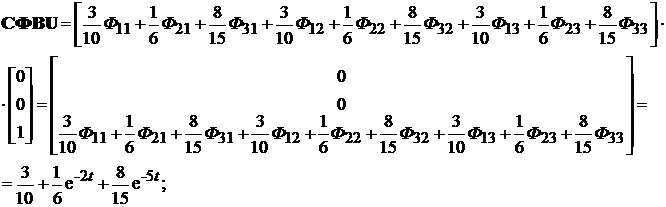
Решение матричного интегрального уравнения

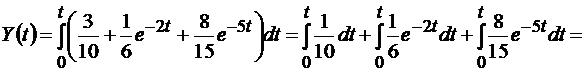
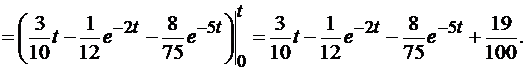
График переходной функции (рис. 4.4) определяют следующим образом

t=0:0.01:1;

y=(3/10)*t-(1/12)*exp(-2*t)-(8/75)*exp(-5*t)+(19/100);

Plot(t,y).

Метод последовательного программирования

Структурную схему для последовательного программирования получают из передаточной функции (4.5), если ее разбить на блоки и для каждого блока представить схему моделирования

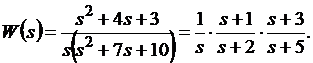(4.11)

По блочной передаточной функции (4.11) составляют схему моделирования (рис. 4.5)

Из схемы моделирования (рис. 4.5) получена матрица коэффициентов состояния Аи матрица коэффициентов наблюдения С

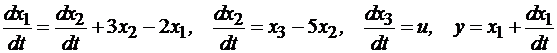
или

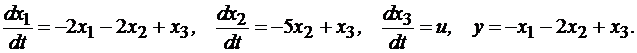
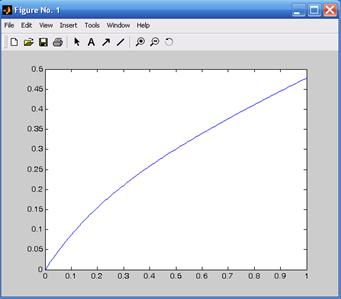
Рис. 4.4. Переходная функция модели, определенная методом параллельного программирования

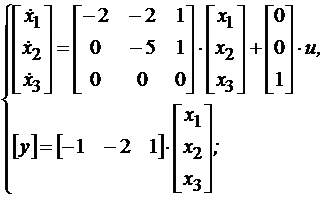(4.12)

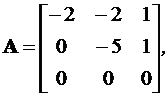
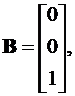C = [-1 -2 1],D = 0.

Определяют фундаментальную матрицу Ф(t):

A=[-2,-2,1;0,-5,1;0,0,0] %Матрица состояния

syms s %Символьная переменная

Is=[s,0,0;0,s,0;0,0,s] %Ввод единичной матрицы

F=inv([Is]-[A]) %Обратная матрица в частотной области

F1=ilaplace(F) %Обратная матрица во временной области.

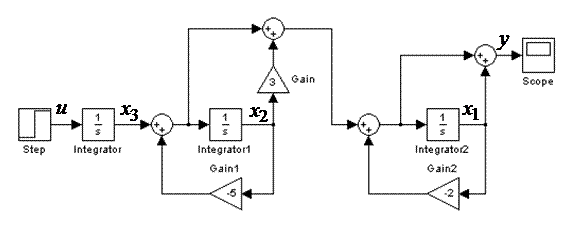
Рис. 4.5 Схема моделирования системы методом последовательного программирования

Фундаментальная матрица в частотной области

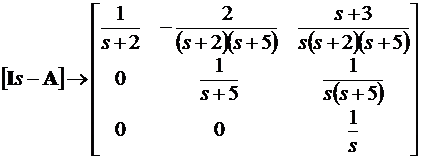
и во временной области

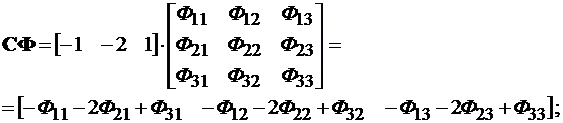
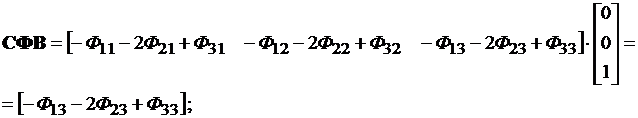
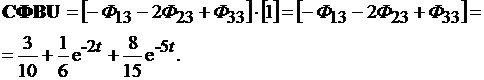
Решение матричного интегрального уравнения

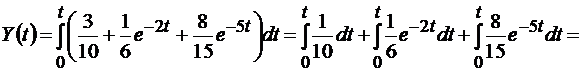
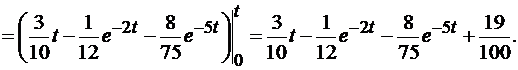
График переходной функции (рис. 4.6) определяют следующим образом

t=0:0.01:1;

y=(3/10)*t-(1/12)*exp(-2*t)-(8/75)*exp(-5*t)+(19/100);

Plot(t,y).

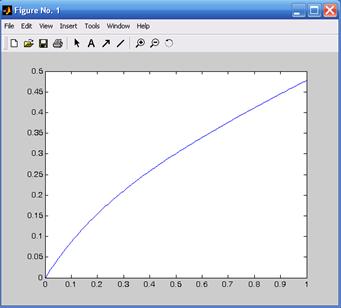
Рис. 4.6. Переходная функция модели по методу последовательного программирования

Задание

1. По полученным в лабораторной работе №3 схемам моделирования заданной передаточной функции и матрицам состояния А для методов прямого, параллельного и последовательного программирования определить обратные матрицы в частотной и временной области.

2. С помощью полученных ранее матриц коэффициентов А, В, С и обратных матриц в частотной и временной области для методов прямого, параллельного и последовательного программирования определить произведение матриц CФBU, используя Matlab.

2. Определить 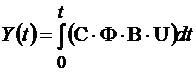для методов прямого, параллельного и последовательного программирования. Построить графики Y(t).

Содержание отчета

1. Структурные схемы исследуемой системы, полученные методами прямого, параллельного и последовательного программирования.

2. Расчет обратных матриц в частотной и временной области для методов прямого, параллельного и последовательного программирования.

3. Расчет выходного сигнала для методов прямого, параллельного и последовательного программирования.

4. Графики выходного сигнала для методов прямого, параллельного и последовательного программирования.

Контрольные вопросы

1. Дайте сравнительную характеристику фундаментальных матриц, полученных по методу параллельного программирования и методу прямого программирования.

2. Дайте сравнительную характеристику фундаментальных матриц, полученных по методу параллельного программирования и методу последовательного программирования.

3. Основные свойства фундаментальной матрицы.

4. С помощью какой команды может быть получена обратная матрица в частотной области?

5. С помощью какой команды может быть получена обратная матрица во временной области?

6. Каким образом с помощью Matlab может получено подинтегральное выражение для определения выходного сигнала системы?

7. Каким образом можно записать фундаментальную матрицу в символьном виде?

Лабораторная работа № 5