Прохождение сигнала и шума через некоторые устройства информационных систем

Модель помехи

В информационных системах (ИС) наряду с полезным сигналом имеют место различного рода помехи. Достаточно распространенными являются помехи в виде случайных процессов с нормальным законом распределения. К таким помехам относятся так называемые внутренние шумы ИС, обусловленные дискретной природой электрического тока, представляющего перемещение элементарных зарядов (к примеру, электронов) в электрических цепях и приборах. Термин «шумы» применительно к помехам впервые появился в телефонии и в дальнейшем стал общепринятым. Из-за дискретной природы электрического тока шум принципиально неустраним.

В качестве модели помехи широко используют белый шум, для которого частотный спектр является сплошным и равномерным на всех частотах 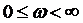(односторонний спектр, используемый в технических расчетах).

Даже в отдельных узлах ИС имеет место несколько источников помех. Обычно их объединяют в один эквивалентный источник помех, включаемый на вход того или иного узла.

Будем рассматривать аддитивную смесь (сумму) помехи (шума) и полезного сигнала, включаемую на вход рассматриваемого узла, принимая его характеристики линейными как для помехи, так и для сигнала.

Прохождение сигнала и шума через измерительный канал

С амплитудной модуляцией

Структурная схема одного из 8 измерительных каналов с амплитудной модуляцией (АМ) аппаратуры 8АНЧ-23 приведена на рис. 3.1.

Рис. 3.1. Структурная схема приема АМ сигнала

При тональной АМ на выходе канала в отсутствие шума сигнал на выходе будет иметь вид: ,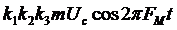

а его эффективное значение равно

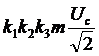, (3.1)

где 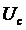– амплитуда немодулированного гармонического переносчика (сигнала);

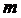– коэффициент АМ ( ).

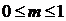Мощность шума на выходе измерительного канала

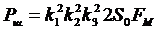, (3.2)

где 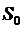– спектральная плотность шума 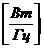. Физически 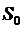есть мощность шума в полосе 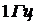, которая не изменяется во всем диапазоне частот. Коэффициент 2 в (3.2) обусловлен удвоением спектральной плотности шума в детекторе.

С учетом (3.2) эффективное напряжение шума, выделяемое на нагрузке 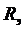, составит

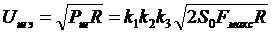. (3.3)

Определяя эффективное напряжение полезного сигнала через его мощность 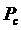на нагрузке 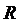из выражений (3.1) и (3.3) и приняв 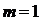, находим относительную среднеквадратическую погрешность в измерительном канале с АМ:

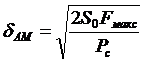. (3.4)

Заметим, что в формуле (3.4) отсутствуют коэффициенты 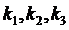, а также сопротивление нагрузки 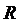. Поэтому в дальнейшем при вычислении погрешностей будем принимать , .

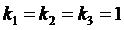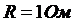Прохождение сигнала и шума через канал

С частотной модуляцией

Структурная схема приема ЧМ колебаний приведена на рис. 3.2. Под действием шума изменяются амплитуда и частота гармонического переносчика. Изменение амплитуды исключается введением ограничителя.

Рассмотрим компоненту входного шума в полосе 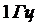на частоте 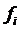с амплитудой .

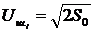Рис. 3.2. Схема приема ЧМ колебаний

Как и ранее, будем считать, что на входе демодулятора ЧМ колебаний напряжение сигнала много больше напряжения шума. Из векторной диаграммы рис. 3.3 найдем

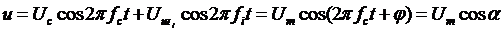, (3.5)

где 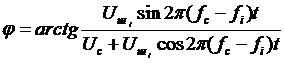; (3.6)

при 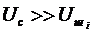из (3.6) получим

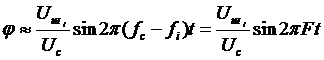, (3.7)

где .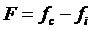

Рис. 3.3. Векторная Рис. 3.4. Спектр шума

диаграмма аддитивной на выходе частотного

смеси сигнала и шума детектора

При изменении 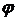(рис. 3.3) амплитуда сигнала 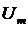остается неизменной и равной напряжению ограничения. Будем считать коэффициент передачи ограничителя равным единице. Тогда круговую частоту на выходе частотного детектора (ЧД), настроенного на среднюю частоту 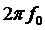, определим как

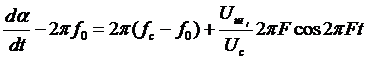
или

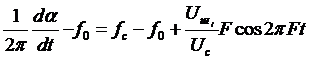, (3.8)

где 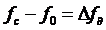– девиация частоты, определяет полезный сигнал на выходе ЧД, а оставшаяся часть (3.8) – шумовую компоненту, эффективное напряжение которой в полосе на выходе ЧД равно:

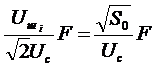. (3.9)

Как и в детекторе АМ колебаний в ЧД спектральная плотность шума удваивается. Поэтому спектральная плотность шумов на выходе ЧД с учетом (3.8) и (3.9) будет

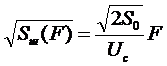, (3.10)

т.е. имеем треугольный спектр шума на выходе ЧД. График 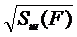показан на рис. 3.4. Используя (3.10), находим эффективное напряжение в полосе пропускания фильтра НЧ от нуля до :

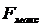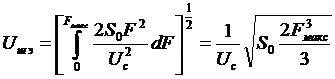. (3.11)

Эффективное напряжение сигнала на выходе ЧД пропорционально 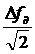, где 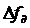– девиация частоты сигнала.

Отношение эффективных напряжений сигнал/шум на выходе фильтра НЧ равно:

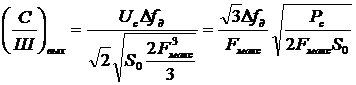, (3.12)

где .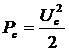

Используя определение индекса модуляции 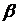в (2.7), из соотношения (3.12) можно найти шумовую относительную среднеквадратическую погрешность для канала с ЧМ:

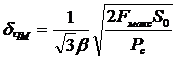. (3.13)

Из соотношений (3.4) и (3.13) находим .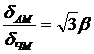

Это уравнение определяет выигрыш ЧМ в отношении 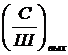по сравнению с АМ. Этот выигрыш обеспечивается за счет более широкой частотной полосы канала с ЧМ, что следует из формул Манаева Е.И. (2.9) и (2.10).