Передача одной боковой полосы

Поскольку спектры боковых частот при АМ симметричны, то с целью уменьшения полосы частот модулированного сигнала обычная модуляция все чаще заменяется передачей одной боковой полосы (ОБП). При однополосной передаче одна из боковых полос и несущая подавляются с помощью фильтров или специальных схем. Такая передача обеспечивает сокращение полосы частот более чем в 2 раза, а за счет отбрасываемых компонент мощность сигнала с ОБП может быть увеличена в несколько раз. В случае ОБП и гармонического модулирующего сигнала (рис. 2.6, а, б) спектр состоит лишь из одной спектральной линии.

а б

Рис. 2.6. График сигнала при ОБП и гармоническом модулирующем сигнале:

а – спектр сигнала с одной боковой полосой,

б – восстановленный модулированный сигнал

Частотная и фазовая модуляция

ЧМ- и ФМ-колебания при тональной модуляции представлены на рис. 2.7. Из рассмотрения этих колебаний можно установить, что когда модулирующий сигнал (рис. 2.7, а) имеет максимальное значение, то у ЧМ-сигнала (рис. 2.7, б) период колебаний минимален, а у ФМ-сигнала фазовое отклонение максимально относительно немодулированной несущей. ЧМ- и ФМ-колебания сохраняют свои амплитуды неизменными.

а

б

Рис. 2.7. Графики сигналов: а – модулирующего, б – при ЧМ

Частотная и фазовая модуляция

Гармоническим сигналом

Выбирая в формуле (2.1) с ЧМ 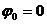, колебание при тональной частотной модуляции можно записать в следующем виде [2]:

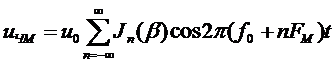, (2.7)

где 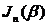– функция Бесселя первого рода порядка n;

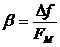– индекс частотной модуляции ( );

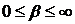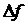– максимальное отклонение или девиация частоты при модуляции относительно частоты .

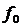Если принять отклонение фазы при ФМ 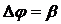, то выражение (2.7) будет справедливо для ФМ-колебаний с тональной модуляцией, что позволило [см. формулы (2.2)] объединить ЧМ и ФМ под одним названием: угловая модуляция. Учитывая это, в дальнейшем будем рассматривать только ЧМ.

На рис. 2.8 приведен спектр ЧМ-колебания. Этот спектр дискретен и состоит из колебаний с несущей частотой 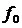, амплитуда которой пропорциональна функции Бесселя нулевого порядка 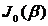и бесконечного числа симметричных боковых частот 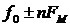с амплитудами, пропорциональными функциям Бесселя соответствующих порядков.

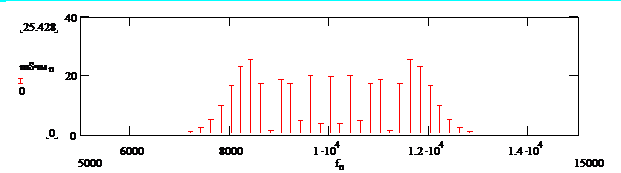Рис. 2.8. Спектр амплитуд частотно-модулированного сигнала

2.8. Частотная манипуляция последовательностью

прямоугольных импульсов

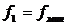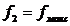Сигнал после частотной манипуляции, используемой в модемах, должен иметь два граничных значения частоты: и . Напряжение, частота которого имеет два значения, показано на рис. 2.9. Такое напряжение можно представить как сумму сигналов 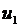и 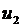с амплитудной манипуляцией ( 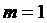), т.е. получающихся от двух генераторов с амплитудной манипуляцией.

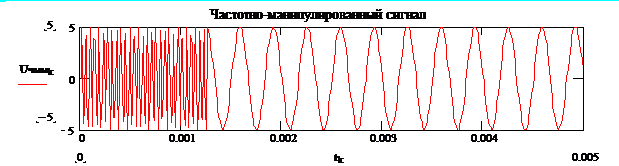
Рис. 2.9. Частотная манипуляция

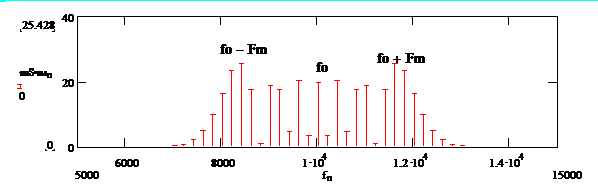Рис. 2.10. Спектр частотно-манипулированного сигнала

Если при частотной манипуляции модулирующим сигналом является последовательность прямоугольных двухполярных импульсов с периодом 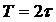, то выражение для частотно-манипулированного без разрыва фазы колебания будет иметь следующий вид:

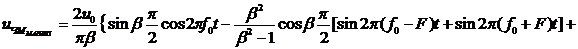
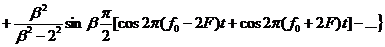, (2.8)

где 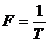– частота следования импульсов;

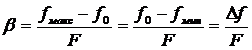– индекс ЧМ при частотной манипуляции.

Из выражения (2.8) следует, что при частотной манипуляции спектр сигнала состоит из колебаний на несущей частоте 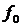и на боковых частотах 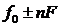, как и в случае гармонического модулирующего сигнала, но амплитуды колебаний другие. На рис. 2.10 приведен характерный спектр сигнала с частотной манипуляцией.