Универсальное множество и дополнение множества

Как правило, при определении конкретного множества явно или неявно (интуитивно) ограничивается собрание допустимых объектов. Например, говоря о слонах, говорят о млекопитающих; говоря о натуральных числах, предполагают задание множества целых или действительных чисел.

Удобно совокупность допустимых объектов зафиксировать и считать, что рассматриваемые множества состоят из элементов этой совокупности. Искомую совокупность называют универсальным множеством или универсумом и обозначают .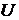

В соответствии с этим любое множество будем рассматривать в связи с универсумом, который при графической иллюстрации будем изображать прямоугольником, а множества будем изображать внутри данного прямоугольника.

В соответствии с введением множества 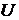разность будем называть дополнением множества (до множества 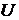) и обозначать .

Симметрическая разность

Симметрической разностью множеств и называется множество, которое обозначается 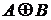(иногда 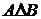) и определенное следующим образом:

.

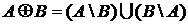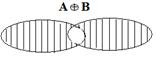
Приведем графическую иллюстрацию операции симметрической разности двух множеств:

Пример. Записать с помощью операций над множествами выражение для множества, соответствующего заштрихованной области диаграммы:

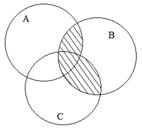
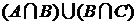► или . ◄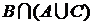

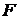Пример. С помощью графической интерпретации изобразить множество , если 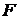образовано множествами , и :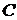

.

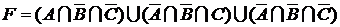► Изобразим множества , и 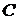на диаграмме Эйлера-Венна, как показано на рисунке ниже.

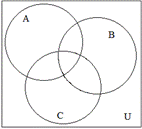
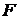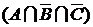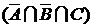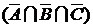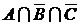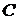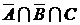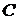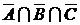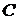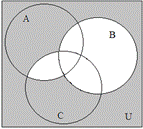
Множество есть объединение трех множеств, , и . Рассмотрим множество . Его элементами являются элементы множества , которые не принадлежат и не принадлежат . Аналогично, множество состоит из элементов , не принадлежащих или . Элементы множества – есть элементы , не принадлежащие ни , ни , ни . Таким образом, множество 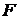на диаграмме Эйлера-Венна имеет вид (заштрихованным областям соответствует серый цвет):

◄

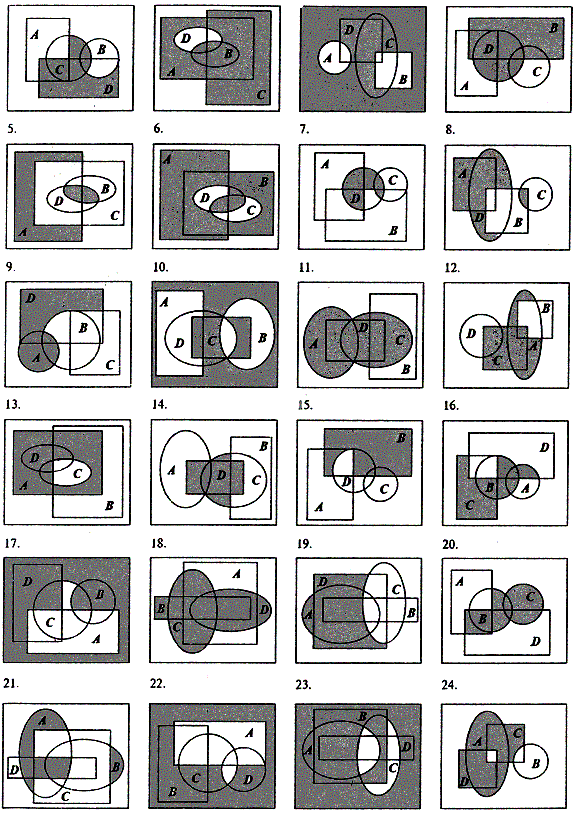
1.2. Задание.

Ниже приведены диаграммы Виенна. Представьте заштрихованную и отдельно незаштрихованную области максимально компактными аналитическими выражениями, в которых бы использовались минимальное количество логических операций и букв. Результаты проверьте по таблицам истинности.

1.3. Контрольные вопросы

1.3.1. Дайте определение конечного множества, элементов множества.

1.3.2. Какие существуют основные способы задания множества?

1.3.3. Какие множества называются равными? Что такое подмножество?

1.3.4. Назовите основные операции над множествами, какой наглядный инструмент используется для иллюстрации операций над множествами?

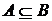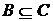1.3.5. Докажите свойство если и , то .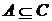

1.3.6. Перечислите свойства операций над множествами, докажите , .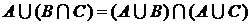

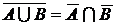1.3.7. Дайте определение прямому (декартовому) произведению множеств;

1.3.8. Записать с помощью операций над множествами выражение для множества, соответствующего закрашенной области диаграммы:

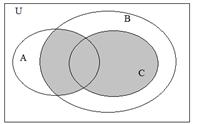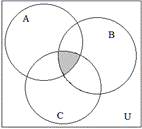
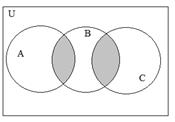
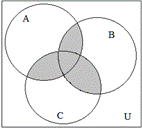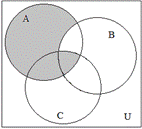1.3.9. С помощью графической интерпретации изобразить множество 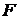, если 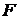образовано множествам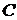и , , и :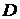

;

;

;

;

;

.

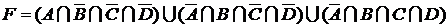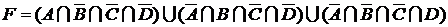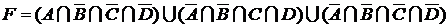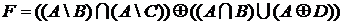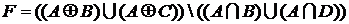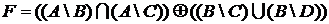1.3.10. Доказать тождества

;

;

;

;

;

;

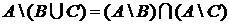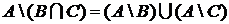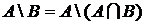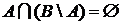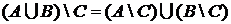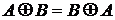Лабораторная работа № 2

Тема: «Алгебра высказываний»

Цель: Приобретение практических навыков работы с алгеброй логики высказываний.

2.1 . Теоретические сведения [1].

Таблицы истинности

Каждая формула алгебры обладает свойством превращаться в высказывание при фиксации в ней значений всех высказывательных переменных, т. е. если мы зафиксируем в формуле значения всех высказывательных переменных, то, пользуясь определениями логических операций, мы можем вычислить значение истинности формулы.

Таблица истинности формулы алгебры высказываний содержит столько строк, сколько всевозможных наборов значений истинности переменных можно образовать. Так как каждая высказывательная переменная может принимать только два значения (0 и 1), то в случае 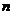переменных таблица истинности содержит 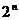строк.

При построении таблицы истинности наборы значений переменных располагают сверху вниз в лексикографическом порядке (каждый набор понимают как двоичную запись неотрицательного целого числа и располагают в порядке возрастания от (000 … 0) до (111 … 1).

Если у вас возникают трудности с использованием двоичной системы счисления, можно применять метод «последовательного половинного деления столбцов» – столбец первой переменной делят пополам и заполняют верхнюю половину нулями, а нижнюю половину – единицами, затем каждую половину второго столбца делят пополам и опять заполняют полученные половины нулями и единицами, и т. д. Затем в соответствии с порядком действий последовательно заполняют столбцы значений подформул, из которых образуется формула. Последним заполняется столбец значений истинности формулы.

Пример.Построить таблицу истинности формулы: .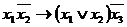

1. Определить порядок действий в формуле:

.

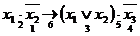2. Пользуясь определениями операци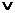й –, &, и 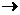, заполним таблицу:

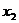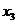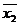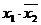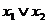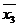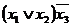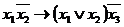Равносильные преобразования и упрощения формул

Ключом к решению примеров на равносильные преобразования и упрощения формул являются 19 основных равносильностей булевой алгебры высказывания (теорема 2.2) [1], поэтому первым шагом при решении таких примеров является переход к булевым операциям с помощью формул:

,

~ .

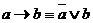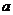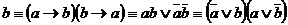Условное решение примера зависит от умелого, эффективного применения основных равносильностей. Следует иметь в виду, что буквы, использованные при записи основных равносильностей, могут означать как символы высказывательных переменных, так и формулы алгебры высказываний, т. е. основная равносильность 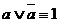означает, в частности, что , , .

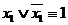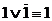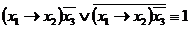Полезными при решении примеров на упрощение формул являются законы полупоглощения:

1) 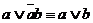; 1’) ;

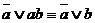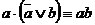2) ; 2’) ,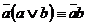

которые мы сейчас докажем.

► .

.◄

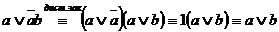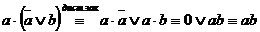Пример.С помощью равносильных преобразований упростить формулу .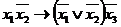

►

◄

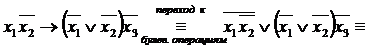
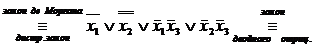
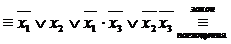
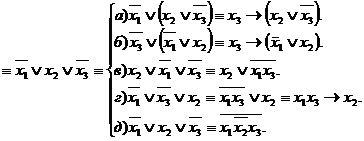Замечание.Любую запись а) - д) можно считать ответом.

Следующий тип параметров – доказательство равносильности двух заданных формул с помощью равносильных преобразований. Существует три основных схемы решения таких примеров. Каждая из них предполагает выполнение перехода к булевым операциям в исходных формулах.

Далее, по первой схеме предполагается, начиная с левой формулы, провести цепочку равносильных преобразований, завершив ее на правой формуле.

Вторая схема – зеркальное отражение первой.

Третья схема предполагает проведение параллельных цепочек равносильных преобразований левой и правой формул до тех пор, пока в этих цепочках не обнаружится совпадение каких-то звеньев (одного звена верхней цепочки с одним звеном нижней).

Пример.Доказать, что .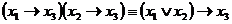

►Перейдем к булевым операциям

.

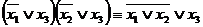1-я схема.

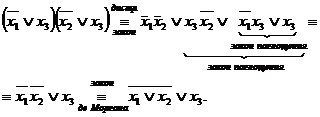
2-я схема

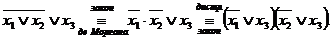
3-я схема

◄

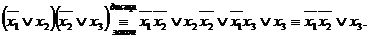
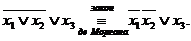Замечание. Следует иметь в виду, что среди примеров на доказательство равносильности формул есть примеры с отрицательным ответом. В этом случае ни одна из схем не приводят к получению ответа. Однако, неудача при использовании схем 1 – 3 может говорить и о недостаточно высокой технике равносильных преобразований. В случае неудачных попыток применения схем 1 – 3 следует для обеих формул построить таблицы истинности. Совпадение столбцов значений формул будет означать их равносильность, а несовпадение – неравносильность.