Оценка статистической значимости параметров уравнения регрессии.

С помощью МНК можно получить лишь оценки параметров уравнения регрессии. Чтобы проверить, значимы ли параметры (т.е. значимо ли они отличаются от нуля в истинном уравнении регрессии) используют статистические ме­тоды проверки гипотез. В качестве основной гипотезы вы­двигают гипотезу о незначимом отличии от нуля параметра регрессии или коэффициента корреляции. Альтернативной гипотезой, при этом является гипотеза обратная, т.е. о неравенстве нулю параметра или коэффициента корреляции. Для проверки гипотезы используется t-критерий Стьюдента.

Найденное по данным наблюдений значение t-критерия (его еще называют наблюдаемым или фактиче­ским) сравнивается с табличным (критическим) значением, определяемым по таблицам распределения Стьюдента (ко­торые обычно приводятся в конце учебников и практикумов по статистике или эконометрике). Табличное значение оп­ределяется в зависимости от уровня значимости 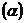и числа степеней свободы, которое в случае линейной парной рег­рессии равно 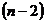, n-число наблюдений.

Если фактическое значение t-критерия больше таб­личного (по модулю), то считают, что с вероятностью 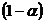параметр регрессии (ко­эффициент корреляции) значимо отличается от нуля.

Если фактическое значение t-критерия меньше таб­личного (по модулю), то нет оснований отвергать основную гипотезу, т.е. параметр регрессии (коэффициент корреля­ции) незначимо отличается от нуля при уровне значимости .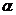

Фактические значения t-критерия определяются по формулам:

,

,

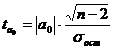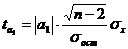где .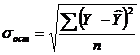

Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции используют критерий:

,

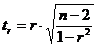где r - оценка коэффициента корреляции, полученная по наблюдаемым данным.

Прогноз ожидаемого значения результативного признака Y по линейному парному уравнению регрессии.

Пусть требуется оценить прогнозное значение призна­ка-результата для заданного значения признака-фактора 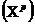. Прогнозируемое значение признака-результата с дове­рительной вероятностью равной 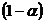принадлежит интервалу прогноза:

,

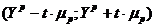где 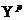- точечный прогноз;

t - коэффициент доверия, определяемый по таблицам распределения Стьюдента в зависимости от уровня значимости α и числа степеней свободы ;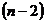

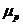- средняя ошибка прогноза.

Точечный прогноз рассчитывается по линейному уравнению регрессии, как:

.

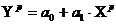Средняя ошибка прогноза определяется по формуле:

.

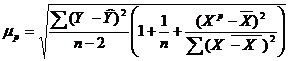Пример 1.

На основе данных, приведенных в Приложении и соответствующих варианту 100, требуется:

1. Построить уравнение линейной парной регрессии одного признака от другого. Один из признаков, соответствующих Вашему варианту, будет играть роль факторного (Х), другой - результативного 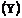. Причинно-следственные связи между признаками установить самим на основе экономического анализа. Пояснить смысл параметров уравнения.

2. Рассчитать линейный коэффициент парной корреляции и коэффициент детерминации. Сделать выводы.

3. Оценить статистическую значимость параметров регрессии и коэффициента корреляции с уровнем значимости 0,05.

4. Выполнить прогноз ожидаемого значения признака-результата Yпри прогнозном значении признака-фактора X, составляющим 105% от среднего уровня X. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал с вероятностью 0,95.

Решение:

В качестве признака-фактора в данном случае выберем курсовую цену акций, так как от прибыльности акций зависит величина начисленных дивидендов. Таким образом, результативным будет признак дивиденды, начисленные по результатам деятельности.

Для облегчения расчетов построим расчетную таблицу, которая заполняется по ходу решения задачи. (Таблица 1)

Для наглядности зависимости Yот X представим графически. (Рисунок 2)

Таблица 1 - Расчетная таблица

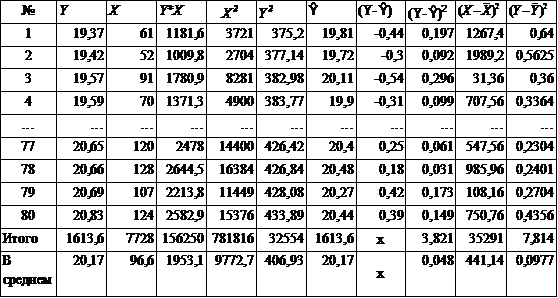
1. Построим уравнение регрессии вида: .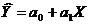

Для этого необходимо определить параметры уравнения 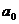и .

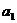Определим ,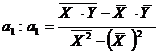

где 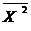- среднее из значений 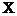, возведенных в квадрат;

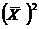- среднее значение 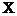в квадрате.

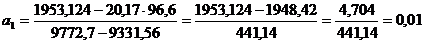
Определим параметр а₀:

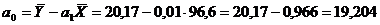
Получим уравнение регрессии следующего вида:

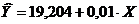
Параметр 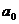показывает, сколько составили бы дивиденды, начисленные по результатам деятельности при отсутствии влияния со стороны курсовой цены акций. На основе параметра 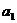можно сделать вывод, что при изменении курсовой цены акций на 1 руб. произойдет изменение дивидендов в ту же сторону на 0,01 млн. руб.

2. Рассчитаем линейный коэффициент парной корреляции и коэффициент детерминации.

Линейный коэффициент парной корреляции определим по формуле:

,

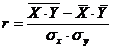Определим 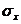и :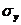

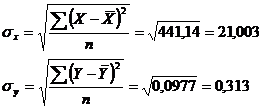
Тогда

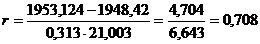
Коэффициент корреляции, равный 0,708, позволяет судить о тесной связи между результативным и факторным признаками .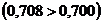

Коэффициент детерминации равен квадрату линейного коэффициента корреляции:

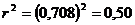
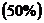
Коэффициент детерминации показывает, что на 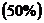вариации начисленных дивидендов зависит от вариации курсовой цены акций, и на 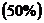- от остальных неучтенных в модели факторов.

3. Оценим значимость параметров уравнения регрессии и линейного коэффициента корреляции по t-критерию Стьюдента. Необходимо сравнить расчетные значения t-критерия для каждого параметра и сравнить его с табличным.

Для расчета фактических значений t-критерия определим :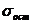

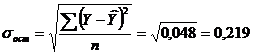
Тогда

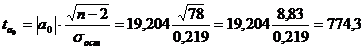
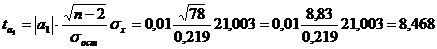
Далее определим 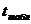_. при уровне значимости 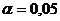и числе степеней свободы равном :

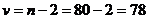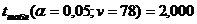
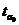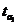Сравним и с 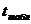: 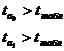, следовательно, оба параметра уравнения регрессии признаются значимыми.

Проверим значимость линейного коэффициента корреляции:

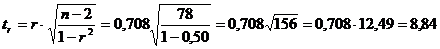
Сравниваем 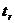с уже известным нам значением 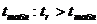, следовательно, линейный коэффициент корреляции существенен.

4. Выполним прогноз ожидаемого значения признака-результата Yпри прогнозном значении признака-фактора X,составляющим 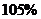от среднего уровня X.

Точечный прогноз рассчитывается по линейному уравнению регрессии:

,

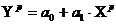В нашем случае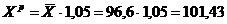

Тогда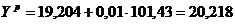

Оценим ошибку прогноза:

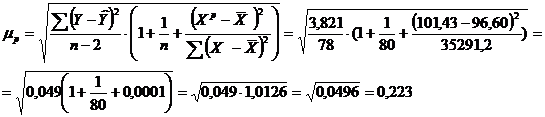
После этого определим интервал, к которому с вероятностью 0,95 принадлежит прогнозное значение признака Y:

,

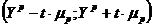где 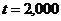– табличное значение t-критерия при 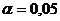и числе степеней свободы

.

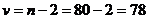В данном случае интервал будет такой:

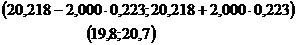
То есть, с вероятностью 0,95 прогнозируемая величина дивидендов при курсовой стоимости акций равной 101,43 руб. будет принадлежать интервалу от 19,8 до 20,7 млн. руб.