Теорема об изменении количества движения точки
Так как масса точки постоянна, а ее ускорение 
то уравнение, выражающее основной закон динамики, можно представить в виде
.
Уравнение выражает одновременно теорему об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна геометрической сумме действующих на точку сил.
Проинтегрируем это уравнение. Пусть точка массы m, движущаяся под действием силы 
(рис.15), имеет в момент t=0 скорость 
, а в момент t1-скорость 
.
Рис.15
Умножим тогда обе части равенства на 
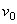и возьмем от них определенные интегралы. При этом справа, где интегрирование идет по времени, пределами интегралов будут 0 и t1, а слева, где интегрируется скорость, пределами интеграла будут соответствующие значения скорости 
и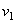 
. Так как интеграл от 
равен 
, то в результате получим:
.
Стоящие справа интегралы представляют собою импульсы действующих сил. Поэтому окончательно будем иметь:
.
Уравнение выражает теорему об изменении количества движения точки в конечном виде: изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов всех действующих на точку сил за тот же промежуток времени (рис. 15).
При решении задач вместо векторного уравнения часто пользуются уравнениями в проекциях.
В случае прямолинейного движения, происходящего вдоль оси Ох теорема выражается первым из этих уравнений.
Вопросы для самопроверки
- Сформулируйте основные законы механики.
- Какое уравнение называется основным уравнением динамики?
- Какова мера инертности твердых тел при поступательном движении?
- Зависит ли вес тела от местонахождения тела на Земле?
- Какую систему отсчета называют инерциальной?
- К какому телу приложена сила инерции материальной точки и каковы ее модуль и направление?
- Объясните разницу между понятиями «инертность» и «сила инерции»?
- К каким телам приложена сила инерции, как направлена и по какой формуле может быть рассчитана?
- В чем заключается принцип кинетостатики?
- Каковы модули и направления касательной и нормальной сил инерции материальной точки?
- Что называют массой тела? Назовите единицу измерения массы в системе СИ?
- Что является мерой инертности тела?
- Запишите основной закон динамики в векторной и дифференциальной форме?
- На материальную точку действует постоянная сила. Как движется точка?
- Какое ускорение получит точка, если на нее действует сила, равная удвоенной силе тяжести?
- После столкновения двух материальных точек с массами m1=6 кг и m2=24 кг первая точка получила ускорение 1,6 м/с. Чему равно ускорение, полученное второй точкой?
- При каком движении материальной точки равна нулю ее касательная сила инерции и при каком – нормальная?
- По каким формулам вычисляются модули вращательной и центробежной сил инерции точки, принадлежащей твердому телу, вращающемуся вокруг неподвижной оси?
- Как формулируется основной закон динамики точки?
- Приведите формулировку закона независимости действия сил.
- Запишите дифференциальные уравнения движения материальной точки в векторной и координатной форме.
- Сформулируйте сущность первой и второй основных задач динамики точки.
- Приведите условия, из которых определяются постоянные интегрирования дифференциальных уравнений движения материальной точки.
- Какие уравнения динамики называются естественными уравнениями движения материальной точки?
- Каковы две основные задачи динамики точки, которые решаются с помощью дифференциальных движений материальной точки?
- Дифференциальные уравнения движения свободной материальной точки.
- Как определяются постоянные при интегрировании дифференциальных уравнений движения материальной точки?
- Определение значений произвольных постоянных, появляющихся при интегрировании дифференциальных уравнений движения материальной точки.
- Каковы законы свободного падения тела?
- По каким законам происходят горизонтальное и вертикальное перемещения тела, брошенного под углом к горизонту в пустоте? Какова траектория его движения и при каком угле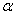 
тело имеет наибольшую дальность полета?
- Как вычислить импульс переменной силы за конечный промежуток времени?
- Что называется количеством движения материальной точки?
- Как выразить элементарную работу силы через элементарный путь точки приложения силы и как – через приращение дуговой координаты этой точки?
- На каких перемещениях работа силы тяжести: а) положительна, б) отрицательна, в) равна нулю?
- Как вычислить мощность силы, приложенной к материальной точке, вращающейся вокруг неподвижной оси с угловой скоростью 
?
- Сформулируйте теорему об изменении количества движения материальной точки.
- При каких условиях количество движения материальной точки не изменяется? При каких условиях не изменяется его проекция на некоторую ось?
- Приведите формулировку теоремы об изменении кинетической энергии материальной точки в дифференциальной и конечной форме.
- Что называется моментом количества движения материальной точки относительно: а) центра, б) оси?
- Как формулируется теорема об изменении момента количества движения точки относительно центра и относительно оси?
- При каких условиях момент количества движения точки относительно оси остается неизменным?
- Как определяются моменты количества движения материальной точки относительно центра и относительно оси? Какова зависимость между ними?
- При каком расположении вектора количества движения материальной точки его момент относительно оси равен нулю?
- Почему траектория материальной точки, движущейся под действием центральной силы, лежит в одной плоскости?
- Какое движение точки называется прямолинейным? Запишите дифференциальное уравнение прямолинейного движения материальной точки.
- Запишите дифференциальные уравнения плоского движения материальной точки.
- Какое движение материальной точки описывают дифференциальные уравнения Лагранжа первого рода?
- В каких случаях материальную точку называют несвободной и каковы дифференциальные уравнения движения этой точки?
- Дайте определения стационарных и нестационарных, голономных и неголономных связей.
- Какие связи называют двусторонними? Односторонними?
- В чем сущность принципа освобождаемости от связей?
- Какой вид имеют дифференциальные уравнения движения несвободной материальной точки в форме Лагранжа? Что называют множителем Лагранжа?
- Приведите формулировку динамической теоремы Кориолиса.
- В чем сущность принципа относительности Галилея-Ньютона?
- Назовите движения, при которых кориолисова сила инерции равна нулю.
- Какой модуль и какое направление имеют переносная и кориолисова силы инерции?
- В чем заключается различие между дифференциальными уравнениями относительного и абсолютного движений материальной точки?
- Как определяются переносная и кориолисова силы инерции в различных случаях переносного движения?
- В чем состоит сущность принципа относительности классической механики?
- Какие системы отсчета называются инерциальными?
- Каково условие относительного покоя материальной точки?
- В каких точках земной поверхности сила тяжести имеет наибольшее и наименьшее значения?
- Чем объясняется отклонение падающих тел к востоку?
- В каком направлении отклоняется тело, брошенное вертикально вверх?
- В шахту опускается бадья с ускорением а=4 м/с2. Сила тяжести бадьи G=2 кН. Определите силу натяжения каната, поддерживающего бадью?
- Две материальные точки движутся по прямой с постоянными скоростями 10 и 100 м/с. Можно ли утверждать, что к этим точкам приложены эквивалентные системы сил?
1) нельзя;
2) можно.
- К двум материальным точкам массой 5 и 15 кг приложены одинаковые силы. Сравните численные значения ускорения этих точек?
1) ускорения одинаковы;
2) ускорение точки массой 15 кг в три раза меньше, чем ускорение точки массой 5 кг.
- Можно ли задачи динамики решать с помощью уравнений равновесия?
1) можно;
2) нельзя.