Закон сохранения количества движения.

Из теоремы об изменении количества движения системы можно получить следую­щие важные следствия:

1) Пусть сумма всех внешних сил, действующих на систему, равна нулю:

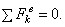
Тогда из уравнения 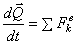следует, что при этом 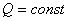. Таким образом, если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянен по модулю и направлению.

2) Пусть внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например Оx) равна нулю:

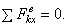
Тогда из уравнения 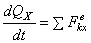следует, что при этом 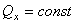. Таким образом, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция количества движения системы на эту ось есть величина постоянная.

33 . Дифференциальные уравнения сферического и свободного движений твердого тела

В случае сферического движения, если в качестве подвижных осей взять главные оси инерции тела и ввести обозначения 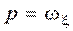, , 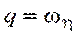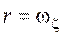; 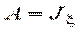, , 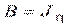, 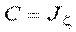то

,

,

.

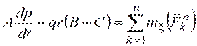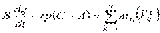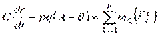Эти уравнения называются динамическими уравнениями Эйлера. Они допускают аналитическое интегрирование при произвольных начальных условиях (определение закона сферического движения твердого тела при известных действующих силах) в трех случаях.

Случай Эйлера–Пуансо. Центр масс тела произвольной формы совпадает с неподвижной точкой. Движение тела происходит по инерции.

Случай Лагранжа–Пуассона. Эллипсоидом инерции для неподвижной точки является эллипсоид вращения 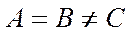и центр масс лежит на оси вращения эллипсоида инерции. (Симметричный волчок).

Случай Ковалевской. Эллипсоид инерции для неподвижной точки есть вытянутый эллипсоид вращения при 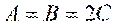.Центр масс тела лежит в экваториальной плоскости эллипсоида инерции. (Асимметричный волчок).

Кинетический момент относительно неподвижной точки и кинетическая энергия твердого тела при сферическом движении определяются выражениями:

,

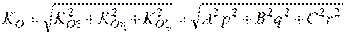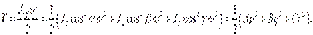
В случае Эйлера–Пуансо два общих интеграла системы дифференциальных уравнений движения твердого тела находятся непосредственно из законов сохранения кинетического момента и энергии

,

.

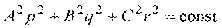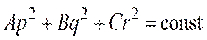Дифференциальные уравнения свободного движения твердого тела нетрудно получить, если рассмотреть движение тела как сложное, принимая за переносное движение поступательное с центром масс, а за относительное – сферическое движение вокруг центра масс. То есть к динамическим уравнениям Эйлера необходимо добавить дифференциальные уравнения движения центра масс

, ,

, ,

, .

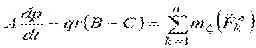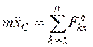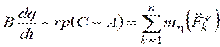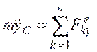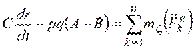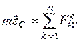34) Мгнове́нный центр скоросте́й — при плоскопараллельном движении точка, обладающая следующими свойствами: а) её скорость в данный момент времени равна нулю; б) относительно неё в данный момент времени вращается тело.

Мгновенный центр скоростей – точка плоской фигуры, скорость которой в данный момент равна нулю – Р. Если тело движется непоступательно, т.е. w¹0, то мгн.цент.ск. всегда существует. При поступательном движении м.ц.с. находится в ¥. 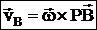– скорость любой точки плоской фигуры имеет модуль, равный произведению угловой скорости фигуры на длину отрезка, соединяющего точку с м.ц.с., и направлена ^ этому отрезку в сторону вращения фигуры. 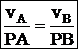, скорости точек тела пропорциональны их расстояниям до м.ц.с. 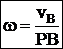, угловая скорость тела равна отношению скорости какой-нибудь точки к ее расстоянию до м.ц.с. Определение положения м.ц.с.: 1) м.ц.с. – точка пересечения перпендикуляров, восстановленных к скоростям точек (напр. в точке В и точке К); 2) если скорости точек А и В параллельны между собой и перпендикулярны АВ, то для определения м.ц.с. должны быть известны модули и направления скоростей (см. v_A и v_B); 3) если они при этом равны между собой, то м.ц.с. находится в ¥, а угловая скорость w=v_A/¥=0; 4) если известно, что скорости двух точек А и В равны, параллельны и не перпендикулярны АВ, то м.ц.с. в ¥, и угловая скорость w=v_A/¥=0, если это имеет место только к некоторый момент времени, то имеем мгновенное поступательное движение; 5) если плоская фигура катится без скольжения по неподвижной поверхности, то м.ц.с. плоской фигуры будет в точке соприкасания.

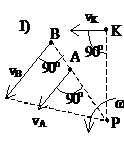
ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ

Мгновенным центром скоростей называется точка плоской фигуры, скорость которой в данный момент времени равна нулю.

Легко убедиться, что если фигура движется непоступательного такая точка в каждый момент времени t существует и притом единственная. Пусть в момент времени t точки А и В плоской фигуры имеют скорост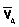и и 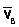, не параллельные друг другу (рис.20). Тогда точка Р, лежащая на пересечении перпендикуляров Аа вектору га и ВЬ к вектору vB, и будет мгновенным центром скоростей так как Vp=0. В самом деле, если допустить, что Vp=0, то по теореме о проекциях скоростей вектор Vp должен быть одновременно перпендикулярен и АР, (так как 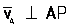) и ВР (так как ), что невозможно. Из той же теоремы видно, что никакая другая точка фигуры в этот момент времени не может иметь скорость, равную нулю.

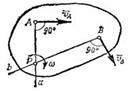
Рис.20

Если теперь в момент времени t взять точку Р за полюс, то скорость точки А будет

,

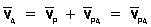так как Vp=0. Аналогичный результат получается для любой другой точки фигуры. Следовательно, скорости точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей. При этом

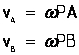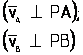, и т.д.

Из равенств, следует еще, что

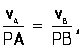
т.е. что скорости точек плоской фигуры пропорциональны их расстояниям от МЦС.

35) Условия равновесия в геометрической и аналитической формах.

Для доказательства условий равновесия воспользуемся основной теоремой статики:

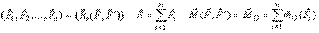(1)

Сформулируем условия равновесия, а затем их докажем.

Для равновесия твердого тела под действием произвольной системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы равнялись нулю:

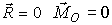(2)

Необходимость условий (2) сразу следует из (1). При выполнении (2) (R,(F,F')) ~ 0 и (F₁, F₂, ..., F_n) ~ 0. Достаточность условий равновесия докажем методом от противного. Предположим, что не выполняются оба условия или хотя бы одно из них, а тело находится в равновесии. Но в этих случаях система сил приводится к двум силам, не лежащим в одной плоскости, или к одной силе, или к одной паре сил, под действием которых твердое тело не может быть в равновесии. Следовательно, наше предположение не верно, а верны условия равновесия (2), достаточность которых доказана.

Условия равновесия (2) являются условиями равновесия в геометрической или в векторной форме. Эти условия широко используются в теоретических доказательствах, однако при решении практических задач они не применяются из-за сложности построения силового и моментного многоугольников в пространстве.

Для получения условий равновесия в аналитической или в координатной форме свяжем с поверхностью Земли или основанием систему координат OXYZ. Центром приведения выберем начало координат O. Спроектируем на оси координат оба векторных выражения в (2). При проектировании учтем, что момент силы относительно оси равен проекции момента относительно центра на оси. В результате получим шесть аналитических выражений:

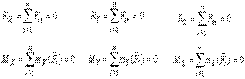(3)

Эти выражения представляют математическую запись условий равновесия произвольной системы сил в аналитической форме.