Вычисление проекций ускорения точки на естественные оси

Пусть движение точки задано в координатной форме. Проекция ускорения на касательную к траектории равна , алгебраическая скорость с точностью до знака равна модулю скорости , а модуль скорости равен

. Вычислим первую производную по времени от этого выражения, получим

Проекция ускорения на нормаль к траектории равна .

3.При векторном способезадания движения поло-

жение точки определяется ее радиусом-вектором r ,

проведенным из некоторой точки О, принимаемой за

начало выбранной системы отсчета (рисунок 1.1).

Уравнение, выражающее зависимость радиус-вектора

точки от времени r r (t)    , называют законом движе-

ния точки в векторной форме.

Для нахождения положения точки при коорди-

натном способе задания ее движения используют

выражения координат как функций времени, например, x = x(t), y = y(t).

Векторный способ. Положение движущейся точки M относительно тела отсчета O можно определить радиус-вектором точки r, соединяющим тело отсчета и точку (рис. 57).

При движении точки M радиус-вектор r будет изменяться по модулю и направлению с течением времени t, то есть

(1)

Выражение (1) определяет закон движения точки и является ее кинематическим уравнением движения в векторной форме.

Конец радиус-вектора совместно с точкой M движется в пространстве по кривой, которая является годографом радиус-вектора, а в кинематике называется траекторией точки. Движение точки по кривой называется криволинейным движением точки, если траектория точки - прямая линия, движение точки называется прямолинейным.

То обстоятельство, что радиус-вектор не связан с конкретной системой координат, позволяет широко использовать векторный способ задания движения для теоретических доказательств.

Для решения практических задач обычно используют координатный и естественный способы задания движения.

При векторном способе задания движения, ускорение точки определяется как первая производная от скорости или вторая производная от радиус-вектора:

А

13.Сложное движение точки (тела) – такое движение, при котором точка (тело) одновременно участвует в нескольких движениях (напр. пассажир, перемещающийся по движущемуся вагону). В этом случае вводится подвижная система координат (Oxyz), которая совершает заданное движение относительно неподвижной (основной) системы координат (O₁x₁y₁z₁). Абсолютным движением точки назыв. движение по отношению к неподвижной системе координат. Относительное движение – движение по отношению к подвижной системе коорд. (движение по вагону). Переносное движение – движение подвижной сист. координат относительно неподвижной (движение вагона). Теорема о сложении скоростей: , ; -орты (единичные вектора) подвижной системы координат, орт вращается вокруг мгновенной оси, поэтому скорость его конца и т.д., Þ: ,

; – относительная скорость.

; переносная скорость: , поэтому абсолютная скорость точки = геометрической сумме ее переносной (v_e) и относительной (v_r) скоростей , модуль: . Теорема о сложении ускорений (теорема Кориолиса):

и т.д. Слагаемые выражения, определяющего ускорения : 1) – ускорение полюса О;

2)

3) – относительное ускорение точки;

4) ,

получаем: .

Первые три слагаемых представляют собой ускорение точки в переносном движении: – ускорение полюса О; – вращательное уск., – осестремительное уск., т.е. . Теорема о сложении ускорений (теорема Кориолиса): , где – ускорение Кориолиса (кориолисово ускорение) – в случае непоступательного переносного движения абсолютное ускорение = геометрической сумме переносного, относительного и кориолисова ускорений. Кориолисово ускорение характеризует: 1) изменение модуля и направления переносной скорости точки из-за ее относительного движения; 2) изменение направления относительной скорости точки из-за вращательного переносного движения. Модуль ускорения Кориолиса: а_с= 2×|w_e×v_r|×sin(w_e^{^}v_r), направление вектора определяется по правилу векторного произведения, или по правилу Жуковского: проекцию относительной скорости на плоскость, перпендикулярную переносной угловой скорости, надо повернуть на 90^о в направлении вращения.

Кориолисово уск. = 0 в трех случаях: 1) w_e=0, т.е. в случае поступательного переносного движения или в момент обращения угл. скорости в 0; 2) v_r=0; 3) sin(w_e^{^}v_r)=0, т.е. Ð(w_e^{^}v_r)=0, когда относительная скорость v_r параллельна оси переносного вращения. В случае движения в одной плоскости – угол между v_r и вектором w_e = 90^о, sin90^o=1, а_с=2×w_e×v_r.

14.ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС СИЛЫ. Силу , не меняя действия на тело, можно перенести в любую точку пространства О, при этом добавляется присоединенная пара, момент которой равен моменту силы относительно точки О (рис. 1):

Рисунок 1.

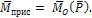ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ В ВЕКТОРНОЙ ФОРМЕ. Выполняется операция параллельного переноса со всеми силами системы. Векторы сил, перенесенных в точку О, посредством построения силового многоугольника, заменяются главным вектором системы сил 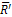, равным их геометрической сумме (рис. 2):

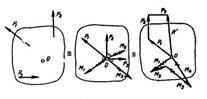
Рисунок 2.

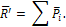Моменты присоединенных пар посредством построения многоугольника моментов заменяются результирующей парой, момент которой - главный момент системы 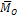равен геометрической сумме моментов присоединенных пар (рис. 2):

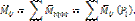Таким образом, при приведении системы сил к данному центру О последняя заменяется мотором - совокупностью скользящего вектора - главного вектора 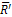и свободного вектора - главного момента .

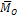ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ В АНАЛИТИЧЕСКОЙ ФОРМЕ. Определение главного вектора системы:

проекции на оси координат:

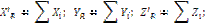модуль

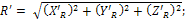направляющие косинусы:

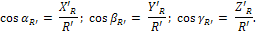Определение главного момента системы:

проекции на оси координат:

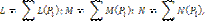где

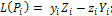
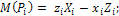
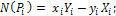
модуль:

направляющие косинусы:

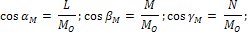угол между 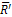и :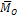

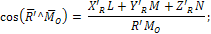линия действия равнодействующей при :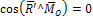

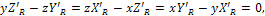где x, у, z - координаты точки на линии действия равнодействующей;

уравнение центральной оси динамы (при ):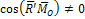

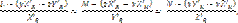где х, y, z - координаты точки на оси динамы;

определение момента динамы:

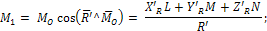условия приведения системы сил к паре:

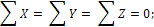условия приведения системы сил к равнодействующей:
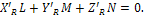