Скорости и ускорения точек тела при вращении.

ПАРА СИЛ

Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.

Плоскостью действия пары сил называется плоскость в которой расположены эти силы.

Плечом пары сил d называется кратчайшее расстояние между линиями действия сил пары.

Моментом пары сил называется вектор 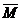, модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия сил пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.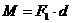

Теорема о сумме моментов пары сил. Сумма моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора этой точки и равна моменту этой пары сил.

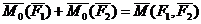
Две пары сил называются эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.

Теорема об эквивалентности пар сил. Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющий одинаковый с первой парой момент.

Теорема о переносе пары сил в параллельную плоскость.Действие пары сил на твердое тело не изменится от переноса этой пары в параллельную плоскость.

Следствие: Момент пары сил, действующий на твердое тело, есть свободный вектор.

Две пары сил, действующих на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению моменты.

Теорема о сложении пар сил.Две пары сил, действующих на одно и то же твердое тело, и лежащие в пересекающихся плоскостях, можно заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.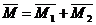

Условия равновесия пар сил.

Если на твердое тело действует несколько пар сил, как угодно расположенных в пространстве, то последовательно применяя правило параллелограмма к каждым двум моментам пар сил, можно любое количество пар сил заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.

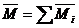
Теорема.Для равновесия пар сил, приложенных к твердому телу, необхо-димо и достаточно, чтобы момент эквивалентной пары сил равнялся нулю.

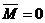
Теорема. Для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций моментов пар сил на каждую из трех координатных осей была равна нулю.

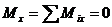
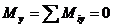
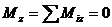
Законы Кулона

1. Сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного скольжения тела под действием активных сил. Сила трения зависит от активных сил, и её модуль заключён между нулём и максимальным значением, которое достигается в момент выхода тела из положения равновесия, то есть:

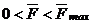
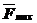- называется предельной силой трения.

2. Предельная сила трения скольжения при прочих равных условиях не зависит от площади соприкосновения трущихся поверхностей. Из этого закона следует, что для того чтобы сдвинуть, например кирпич, надо приложить одну и туже, силу, независимо, от того, какой гранью он положен на поверхность, широкой или узкой.

3. Предельная сила трения скольжения пропорциональна нормальной реакции (нормальному давлению), то есть

,

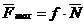где безразмерный коэффициент 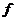называют коэффициентом трения скольжения; он не зависит от нормальной реакции.

4. Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей, то есть от величины и характера шероховатости, влажности, температуры и других условий. Коэффициент трения устанавливается экспериментально.

Считается, что коэффициент трения не зависит от скорости движения.

Векторный способ.

Будем рассматривать случай декартовой прямоугольной системы координат. Движение точки относительно рассматриваемой системы отсчета задано, если известен радиус-вектор 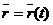этой точки как функция времени, т.е.

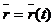(1-1)

Векторный способ обычно применяется для теоретического изложения кинематики точки.

Координатный способ.

Равновесие системы тел.

Рассмотрим равновесие сил, приложенных к системе взаимодействующих между собой тел. Тела могут быть соединены между собой с помощью шарниров или иным способом.

Силы, действующие на рассматриваемую систему тел, можно разделить на внешние и внутренние.

Внешними называются силы, с которыми на тела рассматриваемой системы действуют тела, не входящие в эту систему сил.

Внутренними называются силы взаимодействия между телами рассматриваемой системы.

При рассмотрении равновесия сил, приложенных к системе тел, можно мысленно расчленить систему тел на отдельные твердые тела и к силам, действующим на эти тела, применить условия равновесия, полученные для одного тела. В эти условия равновесия войдут как внешние, так и внутренние силы системы тел. Внутренние силы на основании аксиомы о равенстве сил действия и противодействия в каждой точке сочленения двух тел образуют равновесную систему сил.

Покажем это на примере системы двух тел и плоской системы сил.

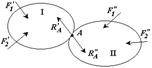Если составить условия равновесия для каждого твердого тела системы тел, то для тела I

.

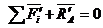
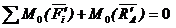для тела II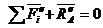

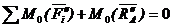
Кроме того, из аксиомы о равенстве сил действия и противодействия для двух взаимодействующих тел имеем .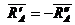

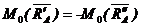Представленные равенства и есть условия равновесия внешних сил, действующих на систему.

Реакция заделки.

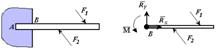Рассмотрим балку один конец которой АВ заделан в стену. Такое крепление конца балки АВ называется заделкой в точке В. Пусть на балку действует плоская система сил. Определим силы, которые надо приложить к точке В балки, если часть балки АВ отбросить. К сечению балки (В) приложены распределенные силы реакции. Если эти силы заменить элементарными сосредоточенными силами и затем привести их к точке В, то в точке В получим силу 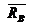(главный вектор сил реакции) и пару сил с моментом М (главный вектор сил реакции относительно точки В) . Момент М называют моментом заделкиилирективным моментом.Силу реакции 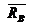можно заменить двумя составляющим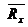и и .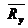

Заделка в отличие от шарнира создает не только неизвестную по величине и направлению реакцию 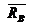, но еще и пару сил с неизвестным моментом М в заделке.

10.Внутренними силами механической системы называются силы взаимодействия между точками и телами рассматриваемой системы.

Равнодействующая всех внутренних сил приложенных к 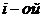точке обозначается 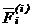(от латинского interior - внутренний).

Это разделение является условным и зависит от того, какая механическая система рассматривается.

Внутренние силы системы обладают следующими свойствами:

Теорема. Главный вектор темы. .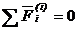

Доказательство: Согласно одной из аксиом динамики, любвсех внутренних сил системы (векторная сумма) равен нулю при любом состоянии сисые две точки системы действуют друг на друга с равными по величине, но противоположно направленными силами. Векторная сумма этих сил равна нулю. Все внутренние силы являются большим количеством таких парных сил. Поэтому сумма всех внутренних сил равна нулю.

Теорема. Главный момент всех внутренних сил системы (векторная сумма) относительно любой точки или оси равен нулю при любом состоянии системы. 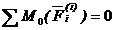или .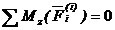

Доказательство: Любые две точки системы действуют друг на друга с равными по величине, но противоположно направленными силами. Сумма моментов этих сил относительно любой точки или оси равна нулю. Все внутренние силы являются большим количеством таких парных сил. Поэтому сумма моментов всех внутренних сил относительно любой точки или оси равна нулю.

Дифференциальные уравнения системы в векторной форме:

,

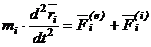Моменты инерции

Для характеристики распределения масс в телах при рассмотрении вращательных движений требуется ввести понятия моментов инерции.

Момент инерции относительно точки

Скалярная величина

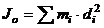или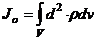

называется полярным моментом инерции относительно точки О. d – расстояние от текущей точки до точки О.

Момент инерции относительно оси

Скалярная величина 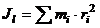или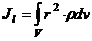

называется моментом инерции относительно оси l. r – расстояние от точки до оси.

Моменты инерции одинаковых по форме однородных тел, изготовленных из разных материалов, отличаются друг от друга. Характеристикой, не зависящей от массы материала, является радиус инерции.

Величина 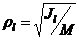называется радиусом инерции.

Момент инерции относительно оси через радиус инерции относительно этой же оси определяется выражением .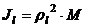

Моменты инерции относительно осей координат

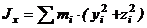
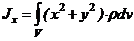
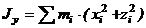
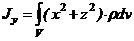
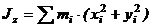
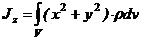
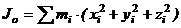
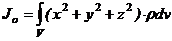
Центробежные моменты инерции

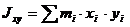
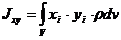
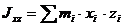
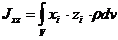
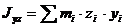
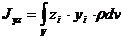
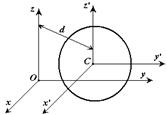
Установим зависимость между моментами инерции относительно параллельных осей, одна из которых проходит через центр масс.

Теорема о моментах инерции относительно параллельных осей. (Теорема Штейнера)

Момент инерции системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы системы на квадрат расстояния между этими осями.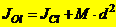

Доказательство: Пусть имеется две декартовы системы координат 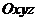и 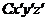, оси которых параллельны. Начало системы 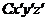находится в центре масс системы. Докажем теорему для осе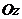й и .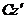

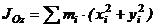
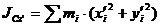
Координаты связаны между собой соотношениями:

, ,

, , .

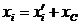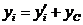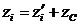
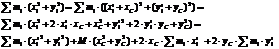
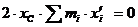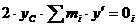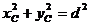Следовательно 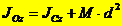, что и требовалось доказать.

Главными осями инерции называются оси, в которых центробежные моменты инерции равны нулю.

Моменты инерции тела относительно главных осей инерции называются главными моментами инерции тела.

Тензор инерции и тензор инерции для главных осей:

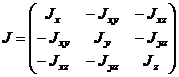
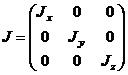
Ускорение точки

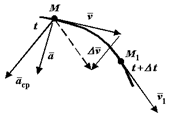Пусть движущаяся точка М в момент времени имеет скорость 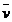. В другой момент времени 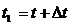эта точка будет занимать положение М₁ и иметь скорость 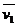. Чтобы изобразить прираще-ние скорости 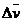за время 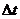, перенесем вектор 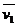параллельно самому себе в точку М.

Рис. 2-3

Средним ускорением точки 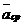за время 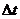называется отношение вектора приращения скорости 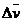к изменению времени .

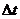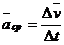(2-3)

Ускорением точки 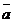в момент времени 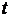называется предел к которому стремится среднее ускорение при 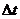, стремящемся к нулю. Ускорение точки равно первой производной по времени от скорости точки или второй производной по времени от радиус-вектора.

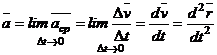(2-4)

Ускорение при координатном способе задания движения

КООРДИНАТНЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ

При координатном способе задания движения:

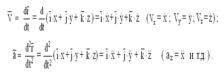
То есть и вектор скорости точки, и вектор ее ускорения при координатном способе задания движения определяются через их проекции на координатные оси. А как найти модуль каждого вектора и его направляющие косинусы, повторять, наверное, не стоит.

Проекция ускорения точки на какую-либо координатную ось равна второй производной по времени от соответствующей координаты этой точки.

Модуль ускорения и направляющие косинусы равны:

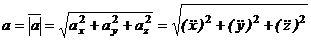(2-8)

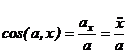
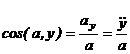
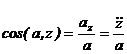(2-9)

Если точка движется в плоскости, то, выбрав оси координат Ox и Oy в этой плоскости, получим:

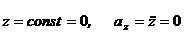
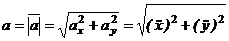
Для прямолинейного движения точки координатную ось, например ось Ox, направляем по траектории. Тогда

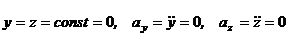
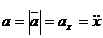
2.Ускорение точки при естественном способе задания движения.

Скорость точки равна .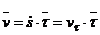

В соответствии с определением ускорения

.

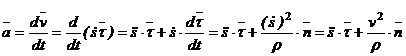Или 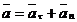(2-10)

Таким образом получено разложение вектора ускорения точки по осям естественного трехгранника.

Часть ускорения 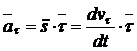(2-11)

называется касательной составляющей ускорения.

Другая часть ускорения 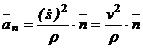(2-12)

называется нормальной составляющей ускорения.Она направлена внутрь вогнутости траектории, т.е. в сторону положительного направления единичного вектора главной нормали .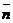

Формулы для проекции ускорения на естественные оси:

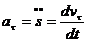
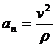
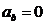
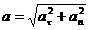
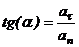
Касательная составляющая 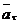, при 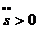направлена по направлению вектора 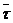, при 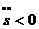противоположно .

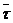Рисунок 1.

ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ В ВЕКТОРНОЙ ФОРМЕ. Выполняется операция параллельного переноса со всеми силами системы. Векторы сил, перенесенных в точку О, посредством построения силового многоугольника, заменяются главным вектором системы сил 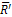, равным их геометрической сумме (рис. 2):

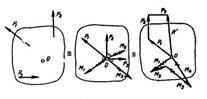
Рисунок 2.

Моменты присоединенных пар посредством построения многоугольника моментов заменяются результирующей парой, момент которой - главный момент системы 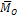равен геометрической сумме моментов присоединенных пар (рис. 2):

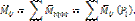Таким образом, при приведении системы сил к данному центру О последняя заменяется мотором - совокупностью скользящего вектора - главного вектора 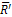и свободного вектора - главного момента .

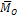ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ В АНАЛИТИЧЕСКОЙ ФОРМЕ. Определение главного вектора системы:

проекции на оси координат:

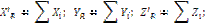модуль

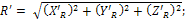направляющие косинусы:

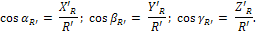Определение главного момента системы:

проекции на оси координат:

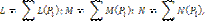где

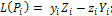
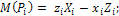
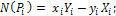
модуль:

направляющие косинусы:

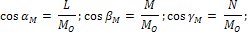угол между и :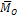

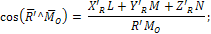линия действия равнодействующей при :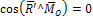

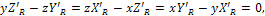где x, у, z - координаты точки на линии действия равнодействующей;

уравнение центральной оси динамы (при ):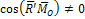

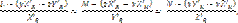где х, y, z - координаты точки на оси динамы;

определение момента динамы:

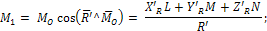условия приведения системы сил к паре:

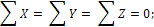условия приведения системы сил к равнодействующей:

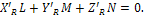Условия равновесия системы

Для равновесия твердого тела под действием произвольной системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы равнялись нулю:

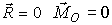1. Для плоской системы сил условие равновесия в аналитической форме имеет вид:

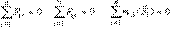(6)

Таким образом, для равновесия твердого тела под действием плоской системы сил необходимо и достаточно, чтобы равнялись нулю две суммы проекций сил на оси координат и сумма алгебраических моментов всех сил относительно любой точки плоскости.

Выражения (6) являются основной формой условия равновесия для плоской системы сил. Существуют еще две дополнительные формы условий, которые мы сформулируем без доказательства.

I-я форма. Для равновесия твердого тела под действием плоской системы сил необходимо и достаточно, чтобы равнялись нулю три суммы моментов сил системы относительно трех точек плоскости, не лежащих на одной прямой:

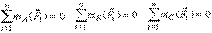(7)

II-я форма. Для равновесия твердого тела под действием плоской системы сил необходимо и достаточно, чтобы равнялись нулю две суммы моментов сил системы относительно двух точек плоскости и сумма проекций сил системы на ось, не перпендикулярную прямой, соединяющей эти точки:

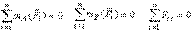2. Для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех прямоугольных осей координат были равны нулю и сумма моментов равна нулю.

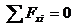
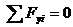
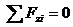
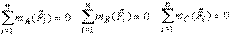
27.

Скорость точки

Одной из основных характеристик движения точки является ее скорость относительно выбранной системы отсчета.

Скорость точки при векторном способе задания движения

Пусть движение точки относительно тела отсчета задано ее радиус-вектором r(t). Тогда, по определению, скоростью точки будет векторная производная радиус-вектора r по скалярному аргументу - времени t:

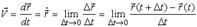	(1)

На рис. 59 изображено как определяется скорость точки. За приращение времени Δt точка переместилась по траектории из положения M в положение M₁, а радиус-вектор получил приращение Δr. Когда Δt 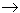0, точка M₁ 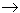M, а вектор Δr, направленный по хорде MM₁, стремится занять положение касательной к траектории. Поэтому вектор скорости V будет направлен, согласно выражению (1), вдоль касательной к траектории в точке M в сторону движения точки.

По определению, вектор скорости является скоростью точки в данное мгновение времени или мгновенной скоростью. Средней скоростью за промежуток времени Δt называется отношение Δr/Δt. Размерность скорости - м/с (метр в секунду), внесистемными единицами скорости могут быть см/с (сантиметр в секунду), км/час (километр в час) и т.д.

Скорость точки при координатном способе задания движения

Пусть движение точки задано в декартовой системе координат Oxyz, которую считаем неподвижной, и известны кинематические уравнения движения точки: x = x(t); y = y(t); z = z(t). Используя равенство (5) в п. 26, по формуле (1) выражаем скорость точки:

Так как система координат Oxyz неподвижна, ее единичные векторы i,j,k постоянны (не меняют ни величину, ни направление), то слагаемые, содержащие производные этих векторов, равны нулю и

(9)

Проекциями вектора скорости на оси координат являются сомножители перед единичными векторами, следовательно,

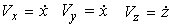
Зная проекции скорости на оси координат, можно определить величину вектора скорости:

(10)

Направление вектора скорости определяется тремя направляющими косинусами:

(11)

Формула (9) позволяет не только определить скорость аналитически, но и построить вектор скорости геометрически. По этой формуле вектор скорости можно представить как сумму трех взаимно перпендикулярных составляющих:

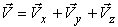(12)

где

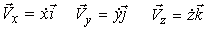(13)

Геометрически сложив составляющие, найдем вектор скорости. При построении составляющих по формулам (21) нужно учитывать: 1) если производная координаты положительна, то направление составляющей совпадает с направлением единичного вектора координатной оси; 2) если производная отрицательна, составляющая направлена в противоположную сторону.

Нахождение скорости при естественном способе задания движения.

При движении точки по траектории радиус-вектор будет меняться с изменением дуговой координаты, а сама дуговая координата является функцией времени, то есть радиус-вектор является сложной функцией времени r = r (s(t)). По формуле (1) выразим вектор скорости точки:

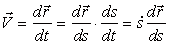(14)

Рассмотрим вектор dr / ds. Согласно формуле (14), этот вектор направлен по касательной к траектории, так как скорость направлена по касательной, а так как 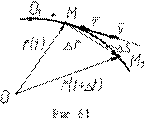приΔs 0 предел отношения длины дуги |Δs| к длине ее хорды MM₁= Δr (рис. 61) равен единице, то по модулю он равен единице. Следовательно,

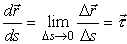(15)

где является единичным вектором касательной к траектории в точке M.

Вектор всегда направлен в сторону возрастания дуговой координаты. На рис. 61 показан случай, когда Δs > 0 (дуговая координата точки больше координаты точки M₁). Сам вектор Δ /Δs направлен в сторону вектора Δ , в сторону положительного отсчета дуги. Когда Δs < 0 , точка M₁ будет находиться ближе к началу отсчета, чем точка M, вектор Δ изменит направление, а вектор Δ /Δs будет направлен в сторону, противоположную Δ (Δs - отрицательное), то есть, по-прежнему, в сторону возрастания дуговой координаты.

Подставляя выражение (15) в формулу (14), получаем

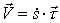(16)

28. Скорость точки при векторном способе задания движения.

Пусть движение точки относительно тела отсчета задано ее радиус-вектором r(t). Тогда, по определению, скоростью точки будет векторная производная радиус-вектора r по скалярному аргументу - времени t:

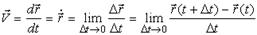(1)

На рис. 59 изображено как определяется скорость точки. За приращение времени Δt точка переместилась по траектории из положения M в положение M₁, а радиус-вектор получил приращение Δr. Когда Δt 0, точка M₁ M, а вектор Δr, направленный по хорде MM₁, стремится занять положение касательной к траектории. Поэтому вектор скорости V будет направлен, согласно выражению (1), вдоль касательной к траектории в точке M в сторону движения точки.

По определению, вектор скорости является скоростью точки в данное мгновение времени или мгновенной скоростью. Средней скоростью за промежуток времени Δt называется отношение Δr/Δt. Размерность скорости - м/с (метр в секунду), внесистемными единицами скорости могут быть см/с (сантиметр в секунду), км/час (километр в час) и т.д.

Определение скорости при координатном способе задания движения.

Пусть движение точки задано в декартовой системе координат Oxyz, которую считаем неподвижной, и известны кинематические уравнения движения точки: x = x(t); y = y(t); z = z(t). Используя равенство (5) в п. 26, по формуле (1) выражаем скорость точки:

Так как система координат Oxyz неподвижна, ее единичные векторы i,j,k постоянны (не меняют ни величину, ни направление), то слагаемые, содержащие производные этих векторов, равны нулю и

(9)

Проекциями вектора скорости на оси координат являются сомножители перед единичными векторами, следовательно,

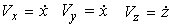
Зная проекции скорости на оси координат, можно определить величину вектора скорости:

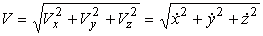(10)

Направление вектора скорости определяется тремя направляющими косинусами:

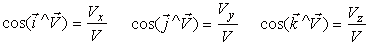(11)

Формула (9) позволяет не только определить скорость аналитически, но и построить вектор скорости геометрически. По этой формуле вектор скорости можно представить как сумму трех взаимно перпендикулярных составляющих:

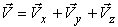(12)

где

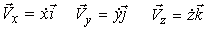(13)

Геометрически сложив составляющие, найдем вектор скорости. При построении составляющих по формулам (21) нужно учитывать: 1) если производная координаты положительна, то направление составляющей совпадает с направлением единичного вектора координатной оси; 2) если производная отрицательна, составляющая направлена в противоположную сторону.

Нахождение скорости при естественном способе задания движения.

При движении точки по траектории радиус-вектор будет меняться с изменением дуговой координаты, а сама дуговая координата является функцией времени, то есть радиус-вектор является сложной функцией времени r = r (s(t)). По формуле (1) выразим вектор скорости точки:

(14)

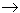Рассмотрим вектор dr / ds. Согласно формуле (14), этот вектор направлен по касательной к траектории, так как скорость направлена по касательной, а так как при Δs 0 предел отношения длины дуги |Δs| к длине ее хорды MM₁ = Δr (рис. 61) равен единице, то по модулю он равен единице. Следовательно,

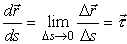(15)

где является единичным вектором касательной к траектории в точке M.

Вектор всегда направлен в сторону возрастания дуговой координаты. На рис. 61 показан случай, когда Δs > 0 (дуговая координата точки больше координаты точки M₁). Сам вектор Δ /Δs направлен в сторону вектора Δ , в сторону положительного отсчета дуги. Когда Δs < 0 , точка M₁ будет находиться ближе к началу отсчета, чем точка M, вектор Δ изменит направление, а вектор Δ /Δs будет направлен в сторону, противоположную Δ (Δs - отрицательное), то есть, по-прежнему, в сторону возрастания дуговой координаты.

Подставляя выражение (15) в формулу (14), получаем

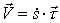(16)

Модуль вектора скорости равен V =| |. Когда > 0, вектор скорости направлен по вектору , когда < 0 , он имеет направление, противоположное вектору .

Величину часто называют алгебраической скоростью точки, считая ее проекцией вектора скорости на касательную к траектории точки.

29.Две основные задачи динамики точки:

1. Первая задача состоит в том, чтобы по заданному закону движения точки массой m определить силу, под действием которой происходит это движение. Часто первую задачу рассматривают как задачу управления движением, в рамках которой требуется установить характеристики воздействия, обеспечивающие заданный закон движения материальной точки. В зависимости от способа задания движения при решении этой задачи используют соответствующие скалярные уравнения.

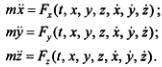(13.3)

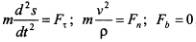
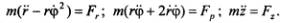
2. Вторая задача состоит в определении движения точки по заданным силам и начальным условиям движения, при этом силы должны быть выражены как функции переменных, используемых для задания движения. Решение этой