Случайные события. Операции над случайными событиями.
Событием называется любой факт, который в результате опыта может произойти или не произойти. Достоверным называется событие, которое происходит в каждом опыте. Невозможным называется событие, которое в результате опыта произойти не может. Несовместными называются события, которые в одном опыте не могут произойти одновременно. Два события называются совместными, если появление одного не исключает появления другого. События A,A1,Am,называются взаимоисключающимися, если любые 2 из них несовместны.
События Ak (k=1, 2, ..., n) образуют полную группу, если они попарно несовместны и в сумме образуют достоверное событие.
Два события называются Противоположным ,если при наступлении одного, второе произойти не может. Два события наз-ся равновозможными, если нельзя считать, что одно из них более возможно, чем другое.
Операции над событиями.
Суммой (объединением) двух событий A и B (A;B) ,называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно. Произведением двух событий A и B ( A×B) называется такое событие, которое заключается в том, что происходят оба события A и B вместе.
Разностьюсобытий А и В называется со-бытие, состоящее в том, что А происходит, а В не происходит.
Свойства.
1. 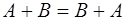 2. 2. 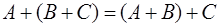 3. 3. 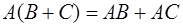 4. 4. 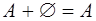 5. 5. 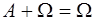 6. 6. 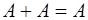 7. 7. 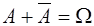 8. 8. 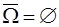 9. 9. 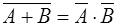 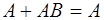 10. 10. 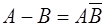 11. 11. 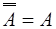 | 1. 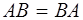 2. 2. 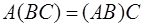 3. 3. 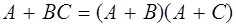 4. 4. 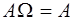 5. 5. 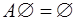 6. 6. 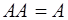 7. 7. 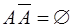 8. 8. 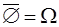 9. 9. 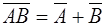 10. 10. 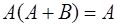 11. 11. 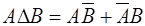 12. 12. 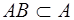 |
Определение вероятности. Относительная частота.
Вероятностью события A называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместных элементарных исходов, образующих полную группу. Наблюдение явления, опыт, эксперимент, которые можно провести многократно, в теории вероятностей принято называть испытанием. Результат, исход испытания называется событием.

Свойство 1. Вероятность достоверного события равна единице
Свойство 2. Вероятность невозможного события равна нулю.
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Относительной частотой события А называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний:
 ,
,
где m – число появлений события А, n – общее число испытаний.
Классическая вероятность вычисляется до опыта, а относительная частота – после опыта.
Геометрические вероятности.
Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности — вероятности попадания точки в область (отрезок, часть плоскости и т. д.).
Пусть случайное испытание можно представить себе как бросание точки наудачу в некоторую геометрическую область G (на прямой, плоскости или пространстве). Элементарные исходы – это отдельные точки G, любое событие – это подмножество этой области, пространства элементарных исходов G. Можно считать, что все точки G «равноправны» и тогда вероятность попадания точки в некоторое подмножество пропорционально его мере (длине, площади, объему) и не зависит от его расположения и формы.
Геометрическая вероятность события А определяется отношением:
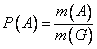 ,
,
где m(G), m(A) – геометрические меры (длины, площади или объемы) всего пространства элементарных исходов и события А.
