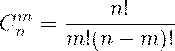Основные правила комбинаторики. Перестановки. Размещения. Сочетания
Основные правила комбинаторики. Перестановки. Размещения. Сочетания
В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов). раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них
Перестановки.Пусть имеется n различных объектов. Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно перестановки, формулы комбинаторики.Pn=n!=1⋅2⋅3⋅...⋅(n−1)⋅n(0!=1,1!=1) 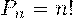
Размещения.размещения, формулы комбинаторики.Пусть имеется n различных объектов. Будем выбирать из них m объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из n объектов по m, а их число равно
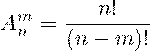
Сочетания.Пусть имеется n различных объектов. Будем выбирать из них m объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из n объектов по m, а их число равно
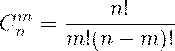
Случайные события. Операции над случайными событиями.
Событием называется любой факт, который в результате опыта может произойти или не произойти. Достоверным называется событие, которое происходит в каждом опыте. Невозможным называется событие, которое в результате опыта произойти не может. Несовместными называются события, которые в одном опыте не могут произойти одновременно. Два события называются совместными, если появление одного не исключает появления другого. События A,A1,Am,называются взаимоисключающимися, если любые 2 из них несовместны.
События Ak (k=1, 2, ..., n) образуют полную группу, если они попарно несовместны и в сумме образуют достоверное событие.
Два события называются Противоположным ,если при наступлении одного, второе произойти не может. Два события наз-ся равновозможными, если нельзя считать, что одно из них более возможно, чем другое.
Операции над событиями.
Суммой (объединением) двух событий A и B (A;B) ,называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно. Произведением двух событий A и B ( A×B) называется такое событие, которое заключается в том, что происходят оба события A и B вместе.
Разностьюсобытий А и В называется со-бытие, состоящее в том, что А происходит, а В не происходит.
Свойства.
1. 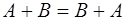 2. 2. 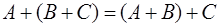 3. 3. 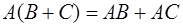 4. 4. 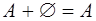 5. 5. 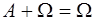 6. 6. 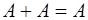 7. 7. 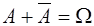 8. 8. 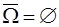 9. 9. 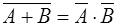 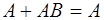 10. 10. 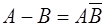 11. 11. 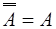 | 1. 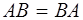 2. 2. 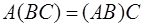 3. 3. 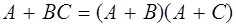 4. 4. 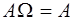 5. 5. 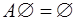 6. 6. 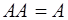 7. 7. 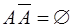 8. 8. 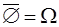 9. 9. 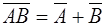 10. 10. 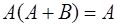 11. 11. 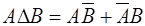 12. 12. 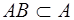 |
Геометрические вероятности.
Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности — вероятности попадания точки в область (отрезок, часть плоскости и т. д.).
Пусть случайное испытание можно представить себе как бросание точки наудачу в некоторую геометрическую область G (на прямой, плоскости или пространстве). Элементарные исходы – это отдельные точки G, любое событие – это подмножество этой области, пространства элементарных исходов G. Можно считать, что все точки G «равноправны» и тогда вероятность попадания точки в некоторое подмножество пропорционально его мере (длине, площади, объему) и не зависит от его расположения и формы.
Геометрическая вероятность события А определяется отношением:
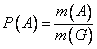 ,
,
где m(G), m(A) – геометрические меры (длины, площади или объемы) всего пространства элементарных исходов и события А.
Доказательство.
Событие 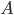 произойдет, если наступит одно из двух несовместных событий:
произойдет, если наступит одно из двух несовместных событий: 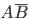 ,
, 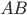 . применяя теорему сложения вероятностей несовместных событий, получаем
. применяя теорему сложения вероятностей несовместных событий, получаем 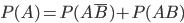 . Откуда
. Откуда
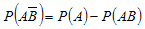 (2.7)
(2.7)
Аналогично для события 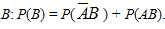 Откуда
Откуда
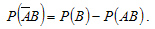 .(2.8)
.(2.8)
Подставив (2.7) и (2.8) в (2.6), находим
P(A+B) = P(A) + P(B) — P(AB)
6. Теорема сложения для несовместных событий:
вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Введем обозначения: n — общее число возможных элементарных исходов испытания; m1 — число исходов, благоприятствующих событию A; m2— число исходов, благоприятствующих событию В.
Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m1 + m2. Следовательно,
Р (A + В) = (m1 + m2) / n = m1 / n + m2 / n.
Приняв во внимание, что m1 / n = Р (А) и m2 / n = Р (В), окончательно получим
Р (А + В) = Р (А) + Р (В).
Следствие 1. Если события 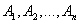 образуют полную группу несовместных событий, то сумма их вероятностей равна единице:
образуют полную группу несовместных событий, то сумма их вероятностей равна единице:
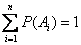 .
.
Доказательство. Так как события 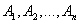 образуют полную группу, то появление хотя бы одного из них – достоверное событие:
образуют полную группу, то появление хотя бы одного из них – достоверное событие:
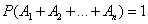 .
.
Так как 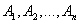 - несовместные события, то к ним применима теорема сложения вероятностей
- несовместные события, то к ним применима теорема сложения вероятностей
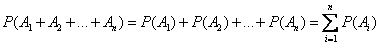 ,
,
откуда
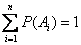
Следствие 2. Сумма вероятностей противоположных событий равна единице:
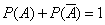 .
.
Это следствие есть частный случай следствия 1. Оно выделено особо ввиду его большой важности в практическом применении теории вероятностей. На практике весьма часто оказывается легче вычислить вероятность противоположного события 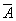 , чем вероятность прямого события
, чем вероятность прямого события 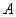 . В этих случаях вычисляют
. В этих случаях вычисляют 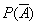 и находят
и находят 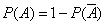
Доказательство
Пусть проводится 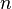 независимых испытаний, причём известно, что в результате каждого испытания событие
независимых испытаний, причём известно, что в результате каждого испытания событие 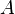 наступает с вероятностью
наступает с вероятностью 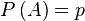 и, следовательно, не наступает с вероятностью
и, следовательно, не наступает с вероятностью 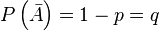 . Пусть, так же, в ходе испытаний вероятности
. Пусть, так же, в ходе испытаний вероятности 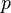 и
и 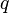 остаются неизменными. Какова вероятность того, что в результате
остаются неизменными. Какова вероятность того, что в результате 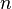 независимых испытаний, событие
независимых испытаний, событие 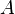 наступит ровно
наступит ровно 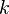 раз?
раз?
Оказывается можно точно подсчитать число "удачных" комбинаций исходов испытаний, для которых событие 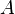 наступает
наступает 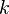 раз в
раз в 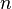 независимых испытаниях, - в точности это количество сочетаний из
независимых испытаниях, - в точности это количество сочетаний из 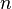 по
по 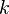 :
:
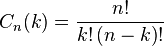 .
.
В то же время, так как все испытания независимы и их исходы несовместимы (событие 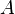 либо наступает, либо нет), то вероятность получения "удачной" комбинации в точности равна:
либо наступает, либо нет), то вероятность получения "удачной" комбинации в точности равна: 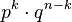 .
.
Окончательно, для того чтобы найти вероятность того, что в 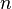 независимых испытаниях событие
независимых испытаниях событие 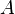 наступит ровно
наступит ровно 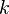 раз, нужно сложить вероятности получения всех "удачных" комбинаций. Вероятности получения всех "удачных" комбинаций одинаковы и равны
раз, нужно сложить вероятности получения всех "удачных" комбинаций. Вероятности получения всех "удачных" комбинаций одинаковы и равны 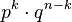 , количество "удачных" комбинаций равно
, количество "удачных" комбинаций равно 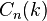 , поэтому окончательно получаем:
, поэтому окончательно получаем:
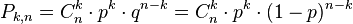 .
.
Формула Пуассон

Локальная теорема Лапласа
. 

Правило трёх сигм.
и рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.
Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:
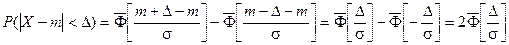
Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:
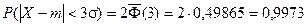
Линейная корреляция.
Корреляционная зависимость между случайными величинами Х и У называется линейной корреляцией, если обе функции регрессии f(y) и g(x) являются линейными.
Рассчитывается по формуле
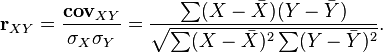
где 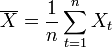 ,
, 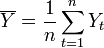 — среднее значение выборок.
— среднее значение выборок.
Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы
Доказательство
Разделив обе части двойного неравенства 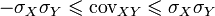 на
на 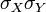 получим
получим
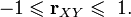
Линейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости: 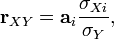 где
где 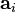 — коэффициент регрессии,
— коэффициент регрессии, 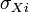 — среднеквадратическое отклонение соответствующего факторного признака.
— среднеквадратическое отклонение соответствующего факторного признака.
ВЫБОРОЧНЫЙ МЕТОД
Часть объектов, которая отобрана для непосредственного изучения из генеральнойсовокупности, называется выборочной совокупностью или выборкой.
Виды выборок
Генеральная совокупность – это совокупность объектов, из которой производится выборка.
Выборочная совокупность (выборка)– это совокупность случайно отобранных объектов.
Объем совокупности – это число объектов этой совокупности. Объем генеральной совокупности обозначается N, выборочной – n.
Вариационный ряд


Интервальное оценивание. Основные понятия

Основные правила комбинаторики. Перестановки. Размещения. Сочетания
В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов). раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них
Перестановки.Пусть имеется n различных объектов. Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно перестановки, формулы комбинаторики.Pn=n!=1⋅2⋅3⋅...⋅(n−1)⋅n(0!=1,1!=1) 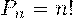
Размещения.размещения, формулы комбинаторики.Пусть имеется n различных объектов. Будем выбирать из них m объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из n объектов по m, а их число равно
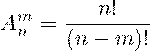
Сочетания.Пусть имеется n различных объектов. Будем выбирать из них m объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из n объектов по m, а их число равно