Скалярное произведение перпендикулярных векторов равно нулю.
Если 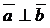 , то
, то 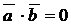 , т.к.,
, т.к., 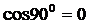 .
.
8) Свойство коллинеарных векторов.
Соответствующие координаты коллинеарных векторов пропорциональны.
Если  и
и 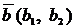 - коллинеарны, то
- коллинеарны, то 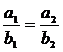 , аналогично, в пространстве: если
, аналогично, в пространстве: если 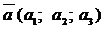 и
и 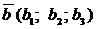 - коллинеарны, то
- коллинеарны, то 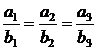 .
.
9) Свойство компланарных векторов.
На свойстве 4 смешанного произведения и формуле (3) основано
условие компланарности трех векторов: Если 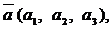
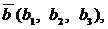
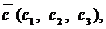 - компланарные, то
- компланарные, то 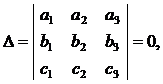
иначе, если 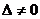 , то говорят, что данные векторы линейно независимы и образуют базис.
, то говорят, что данные векторы линейно независимы и образуют базис.
«Линейное пространство. Базис и ранг системы векторов»
Рассмотрим множество Е произвольной природы с элементами x, y. z.Пусть на множестве Е введены операции сложения и умножения на скаляр, т. е., для любых x, y 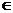 Е определено x+y
Е определено x+y 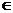 Е и для любых x
Е и для любых x 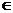 E и
E и 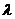
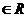 определено
определено 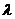 x
x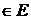 . И эти операции на Е имеют свойства: х+у=у+х, (х+у)+z=х+(у+z),
. И эти операции на Е имеют свойства: х+у=у+х, (х+у)+z=х+(у+z), 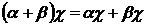 ,
,  (х+у)=
(х+у)=  х+
х+  у;
у; 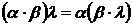 , где
, где 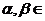 R.
R.
А также существует нулевой элемент 0 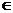 Е, такой, что х+0=0+х=х.
Е, такой, что х+0=0+х=х.
И для любого х 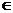 Е существует противоположный ему элемент z
Е существует противоположный ему элемент z 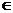 E, такой, что х+z=z+x=0.
E, такой, что х+z=z+x=0.
И существует единичный элемент I 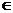 R, такой, что для любого х
R, такой, что для любого х 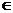 Е х×I=I×x=x.
Е х×I=I×x=x.
Если для множества Е выполняются все вышеперечисленные условия, то множество Е называют линейным пространством.
Нетрудно увидеть, что множество векторов как раз и имеет указанные свойства. Потому элементы линейного пространства Е будем называть векторами: 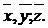
А само пространство будем называть векторным.
Пусть заданы n векторов 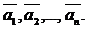 Заданное множество векторов называют системой векторов. Вектор
Заданное множество векторов называют системой векторов. Вектор 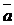 называют линейной комбинацией векторов
называют линейной комбинацией векторов 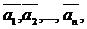 если при любых числах
если при любых числах 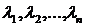 имеет место равенство
имеет место равенство
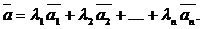
Линейную комбинацию, все коэффициенты которой 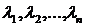 равны нулю, принято называть тривиальной. Иначе, линейная комбинация называется нетривиальной.
равны нулю, принято называть тривиальной. Иначе, линейная комбинация называется нетривиальной.
Система из n 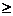 2 векторов называется линейно зависимой, если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору, иначе, система векторов называется линейно независимой.
2 векторов называется линейно зависимой, если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору, иначе, система векторов называется линейно независимой.
Рангом системы называется максимальное число векторов, образующих линейно независимую систему.
Теорема 1.Система из n 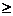 2 векторов линейно зависима тогда, когда хотя бы один из векторов является линейной комбинацией остальных.
2 векторов линейно зависима тогда, когда хотя бы один из векторов является линейной комбинацией остальных.
Теорема 2. Система векторов, содержащая нулевой вектор, линейно зависима.
Теорема 3. Система векторов ранга r, содержащая более r векторов, линейно зависима.
Теорема 4. Система из двух векторов линейно зависима тогда и только тогда, когда эти векторы коллинеарны.
Систему компланарных векторов, среди которых хотя бы два не являются коллинеарными, будем называть системой векторов на плоскости, а систему векторов, среди которых хотя бы одна тройка не является компланарной, - системой векторов в пространстве.
Из рассмотренных выше теорем следует:
1) ранг системы векторов на плоскости равен двум;
2) ранг системы векторов в пространстве равен трем.
