Заданными в координатной форме
УЧЕБНЫЙ КОМПЛЕКС
ПРЕДМЕТ:
«ВЫСШАЯ МАТЕМАТИКА»
ТЕМА № 2.
«ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ».
Преподаватель Кононова М.П.
I. «ВЕКТОРЫ НА ПЛОСКОСТИ
И В ПРОСТРАНСТВЕ».
МАТЕРИАЛ ДЛЯ САМОСТОЯТЕЛЬНОГО
ПОВТОРЕНИЯ И ИЗУЧЕНИЯ.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Тема «Векторы на плоскости и в пространстве» достаточно полно и подробно изучается в школьном курсе математики, причем, отдельно рассматриваются вопросы, связанные со свойствами векторов на плоскости, и затем расширяются знания о векторах при рассмотрении свойств векторов в пространстве.
Именно поэтому студентам предлагается самостоятельно повторить уже изученный материал по приведенным вопросам:
1.Определение вектора, его изображение и обозначение.
2.Основные виды векторов (определения и изображение).
3.Абсолютная величина вектора, направляющие косинусы вектора.
4.Координаты вектора – определение, правило нахождения, примеры.
5.Действия над векторами, заданными своими координатами (правила и примеры).
6.Свойства перпендикулярных, коллинеарных и компланарных векторов (теоремы и примеры на применение).
7.Орты на плоскости и в пространстве (определения и изображение)
Для составления конспекта, который затем используется при выполнении практического задания, и не только, студентам предлагается использовать как учебную литературу по высшей математике, так и школьные учебники. Однако, кроме ранее изученных вопросов, в перечень входят вопросы, непредусмотренные школьной программой, их немного, они достаточно просты для понимания и изучения.
Предлагаемый текст не содержит примеров. Студенты должны самостоятельно подобрать примеры к рассматриваемым определениям, теоремам, свойствам.
Данная тема также используется при решении задач по теме «Аналитическая геометрия», что позволяет также проследить связь между разделами математики, и показать, что всегда можно найти более простой способ решения той или иной задачи.
ВВЕДЕНИЕ.
Понятие вектора находит свое применение и в математике, и в физике, и в других науках.
Знакомство с ними началось еще в школе: рассматривались векторы на плоскости, а затем и в пространстве.
При изучении различных разделов физики, механики и других технических дисциплин встречаются величины, которые вполне характеризуются заданием их численных значений – это так называемые скалярные («скаляр» - латинское - «число») величины. Существуют, однако, и такие величины, для определения которых задания только их численных значений недостаточно. Необходимо также знать их направления в пространстве – эти величины называют векторными.
Примеры:
Скалярные величины – длина, площадь, объем, масса, температура.
Векторные величины – сила, скорость, ускорение, напряженность магнитного поля.
ПОНЯТИЕ ВЕКТОРА.
 Вектор – это направленный отрезок, т.е., отрезок, один конец которого считают его началом, а другой – концом (его указывают стрелкой).
Вектор – это направленный отрезок, т.е., отрезок, один конец которого считают его началом, а другой – концом (его указывают стрелкой).
Основные определения:
1) Абсолютной величиной, или модулем, вектора называется длина отрезка, изображающего вектор:  .
.
2) Вектор, конец и начало которого совпадают, называется нулевым – обозначается  , его абсолютная величина
, его абсолютная величина  .
.
3) Векторы  и
и  называются одинаково (противоположно)направленными, если полупрямые АВ и CD одинаково (противоположно) направлены
называются одинаково (противоположно)направленными, если полупрямые АВ и CD одинаково (противоположно) направлены  ,
,  .
.
4) Два ненулевых вектора называются равными, если они равны по абсолютной величине и одинаково направлены: 
 ,
, 
5) Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
6) Три ненулевых вектора называются компланарными, если они параллельны одной плоскости.
7) Углом между двумя векторами называется угол между пересекающимися прямыми, параллельными этим векторам.
8) Косинусы углов между векторами  и базисными векторами
и базисными векторами  называются направляющими косинусами вектора
называются направляющими косинусами вектора  и вычисляются по формулам
и вычисляются по формулам
 |
Направляющие косинусы любого вектора  связаны равенством
связаны равенством
 |
9) Единичным вектором называется вектор, абсолютная величина которого равна 1.
10)
 Векторы
Векторы  – называют ортами (или базисными), если они единичные, т.е.,
– называют ортами (или базисными), если они единичные, т.е.,
 , а
, а
их направления совпадают с положительными направлениями осей координат:
 .
.
ДЕЙСТВИЯ НАД ВЕКТОРАМИ.
А). Действия над векторами - геометрические.
1. Сложение векторов.
а) правило «треугольника»

 б) вычитание векторов
б) вычитание векторов
в) правило «параллелограмма»

г) правило «параллелепипеда» - для сложения трех некомпланарных векторов:
 Если
Если  - три ненулевых некомпланарных вектора,
- три ненулевых некомпланарных вектора,
то любой вектор  в пространстве может быть представлен в виде:
в пространстве может быть представлен в виде:
 , где
, где
x, y, z – единственная тройка чисел – такое равенство называется разложением вектора по некомпланарным векторам.
Некомпланарными можно считать и базисные векторы  , их координаты
, их координаты
 , тогда получаем следующее разложение вектора по базису:
, тогда получаем следующее разложение вектора по базису:

2. Умножение вектора на число.


Произведением ненулевого вектора  на
на  , есть вектор
, есть вектор  , имеющий направление вектора
, имеющий направление вектора  , если
, если  , и противоположно направлен вектору
, и противоположно направлен вектору  , если
, если  ; абсолютная величина этого вектора равна абсолютной величине вектора
; абсолютная величина этого вектора равна абсолютной величине вектора  , умноженной на
, умноженной на  .
.
| СВОЙСТВА: | |
| Сложения | Произведения на число |
1.  | 1.  |
2.  | 2.  |
3.  | 3.  |
4.  |
Б). Векторы в прямоугольной системе координат.
Пусть 0ху – прямоугольная система координат, в которой заданы своими координатами точки  . Тогда координатами вектора
. Тогда координатами вектора  будут числа
будут числа  , т.е.,
, т.е., 
Если 0xyz – прямоугольная система координат в пространстве, то, если  то вектор имеет такие координаты:
то вектор имеет такие координаты:  .
.
Т.е., чтобы найти координаты вектора, заданного координатами своих начала и конца, надо из каждой координаты конца вектора вычесть соответствующую координату начала вектора.
В). Действия с векторами,
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
№ 1 а) Длина вектора на плоскости находится по одной из формул:
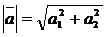 , где
, где 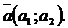 .
.
или 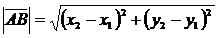 , где
, где 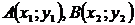 .
.
Найти длину вектора:
1) 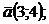 2)
2) 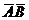 , где
, где 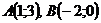 .
.
б) Длина вектора в пространстве находится по одной из формул:
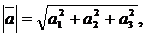 где
где 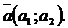
или 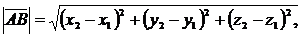 где
где 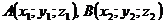 .
.
Найти длину вектора:
1) 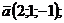 2)
2) 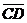 , где
, где 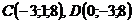 .
.
№ 2 Направляющими косинусами вектора 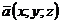 называются числа
называются числа 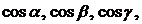 где
где
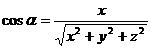 ;
; 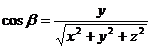 ;
; 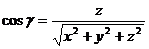 .
.
Найти длину вектора 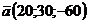 и его направляющие косинусы.
и его направляющие косинусы.
№ 3 Скалярным произведением векторов 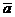 и
и 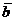 называется число, равное произведению их длин на косинус угла между ними:
называется число, равное произведению их длин на косинус угла между ними:
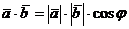 .
.
Если векторы заданы в координатной форме, то скалярное произведение находят по формуле:
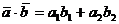 , если
, если 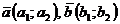
или 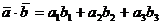 , если
, если 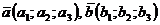
Найти скалярное произведение векторов:
1) 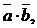 если
если 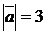 ,
, 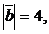
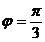 .
.
2) 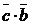 , если
, если 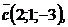
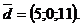
№ 4 Для нахождения угла между векторами используют одну из формул:
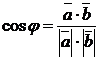 или
или 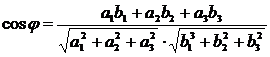 или
или
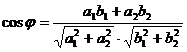
Найти угол между векторами:
1) 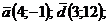
2) 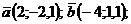
3) 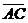 и
и  где А(6;-2), В(-4;8), С(0;-4), D(6;0).
где А(6;-2), В(-4;8), С(0;-4), D(6;0).
№ 5 Правило умножения вектора на число:
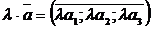 .
.
Правило сложения векторов:
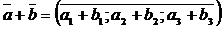
Выполнить действия: 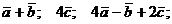
где 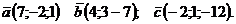
№ 6 Базисом 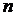 - мерного пространства
- мерного пространства 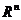 называют множество
называют множество 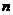 линейно независимых векторов
линейно независимых векторов 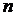 - мерного пространства. Векторы
- мерного пространства. Векторы 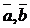 и
и 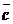 линейно независимы, если определитель, составленный из их координат, отличен от нуля:
линейно независимы, если определитель, составленный из их координат, отличен от нуля:
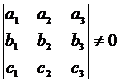
Разложить вектор 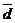 по базису – значит представить этот вектор как линейную комбинацию базисных векторов:
по базису – значит представить этот вектор как линейную комбинацию базисных векторов: 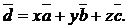
Для нахождения неизвестных чисел 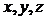 необходимо составить систему линейных алгебраических уравнений и решить ее любым способом.
необходимо составить систему линейных алгебраических уравнений и решить ее любым способом.
Проверить, составляют ли векторы 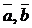 и
и 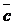 базис в пространстве R3 и найти координаты вектора
базис в пространстве R3 и найти координаты вектора 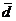 в этом базисе:
в этом базисе:
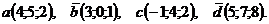
№ 7 Два вектора 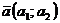 и
и 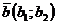 или
или 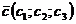 и
и 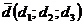 перпендикулярны, если их скалярное произведение равно 0.
перпендикулярны, если их скалярное произведение равно 0.
а) Перпендикулярны ли векторы:
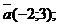
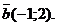
б) При каком х перпендикулярны векторы 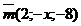 и
и 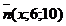 ?
?
№ 8 Два вектора 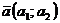 и
и 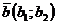 или
или 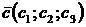 и
и 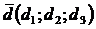 коллинеарны, если их соответствующие координаты пропорциональны, т.е.
коллинеарны, если их соответствующие координаты пропорциональны, т.е. 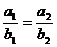 или
или 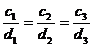 .
.
а) Коллинеарны ли векторы
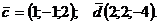
б) При каком m коллинеарны векторы 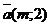 и
и 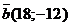 ?
?
НА ПЛОСКОСТИ»
Уравнение кривой линии»
Уравнение линии является важнейшим понятием аналитической геометрии.

Пусть на плоскости задана некоторая кривая линия. Координаты х и у точки, лежащей на этой линии, связаны определенным образом. Такая связь аналитически записывается в виде некоторого уравнения.
ОПРЕДЕЛЕНИЕ. Уравнением кривой линии на плоскости Оху называется уравнение, которому удовлетворяют координаты х и у каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Общий вид такого уравнения:
 .
.
Если точка М (х; у) передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты М (х; у) называются текущими координатами.
Установленная связь между линиями и их уравнениями позволяет изучать свойства линий путем анализа уравнений, соответствующих этим линиям. Отсюда и название предмета – аналитическая геометрия.
Уравнение прямой»
ОПРЕДЕЛЕНИЕ. Уравнение первой степени относительно переменных
х и у вида
Ах+Ву+С=0
при условии, что коэффициенты А и В одновременно не равны нулю, называется общим уравнением прямой.
Виды уравнения прямой
| Способ задания прямой | Вид уравнения | Пример |
1. Уравнение прямой с угловым коэффициентом -  , где , где  - угол, образованный прямой с положительным направлением оси Ox, прямая пересекает ось Oy в точке (0;b) - угол, образованный прямой с положительным направлением оси Ox, прямая пересекает ось Oy в точке (0;b) |  | Дано:  . Составить уравнение прямой и построить её. . Составить уравнение прямой и построить её. |
2. Уравнение прямой с угловым коэффициентом  , прямая проходит через точку (x0;y0) , прямая проходит через точку (x0;y0) |  | |
| 3. Уравнение прямой в отрезках – прямая пересекает ось Ox в точке (a, 0) и ось Oy в точке (0;b) |  , ,  | |
4. Уравнение прямой, проходящей через две точки  и и  (несовпадающие) (несовпадающие) |  | |
5. Уравнение прямой, проходящей через заданную точку  параллельно направляющему вектору параллельно направляющему вектору  |  , ,  | |
6. Уравнение прямой, проходящей через данную точку  перпендикулярно нормальному вектору перпендикулярно нормальному вектору  |  | |
| 7.Уравнение прямой, проходящей через начало координат |  | |
8.Уравнение прямой, параллельной: оси  оси оси  |  | |
9.Уравнение прямой, совпадающей: с осью  с осью с осью  |  | |
10. Уравнение пучка прямых, проходящих через точку  |  , где , где  - произвольное число, кроме - произвольное число, кроме  |
I. Прикладные задачи.
v Деление отрезка в заданном отношении.
Точки  и
и  являются концами отрезка
являются концами отрезка  , а точка
, а точка  Î
Î  делит его в отношении
делит его в отношении  , т.е.
, т.е.  .Координаты
.Координаты  точки
точки  находят по формулам:
находят по формулам: ;
;  .Если же
.Если же  то получаем формулы для нахождения координат середины отрезка АВ:
то получаем формулы для нахождения координат середины отрезка АВ: 
I. Прямая в пространстве
 Если прямая в пространстве параллельна некоторому вектору
Если прямая в пространстве параллельна некоторому вектору  (направляющему) и проходит через точку
(направляющему) и проходит через точку  , то ее уравнения можно получить из условия коллинеарности векторов
, то ее уравнения можно получить из условия коллинеарности векторов
 и
и  ,
,
где  - произвольная точка:
- произвольная точка:
 (*)
(*)
Эти уравнения (*) называются каноническими уравнениями прямой линии в пространстве.
Обозначим через t общее значение отношений канонических уравнений данной прямой:
 .
.
Из получившегося равенства получаем:  (**)
(**)
Эти уравнения (**) называют параметрическими уравнениями прямой в пространстве, которая проходит через точку  параллельно вектору
параллельно вектору
 . Переменную t рассматривают как параметр, который произвольно изменяется в интервале
. Переменную t рассматривают как параметр, который произвольно изменяется в интервале  . Координаты точки
. Координаты точки  зависят от параметра t, поэтому при изменении t точка
зависят от параметра t, поэтому при изменении t точка  двигается по данной прямой.
двигается по данной прямой.
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Даны четыре точки М 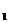 , М
, М 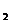 , М
, М 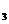 , М
, М 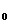 . Требуется:
. Требуется:
1) написать уравнение плоскости Р, проходящей через точки М 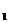 , М
, М 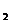 , М
, М 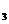 ;
;
2) преобразовать полученное уравнение плоскости Р в уравнение плоскости в отрезках и построить эту плоскость;
3) найти расстояние от точки М 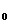 до плоскости Р.
до плоскости Р.
а) М 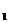
 , М
, М 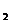
 , М
, М 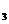
 , М
, М 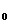
 ;
;
б) М 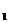
 , М
, М 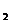
 , М
, М 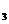
 , М
, М 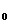
 ;
;
в) М 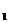
 , М
, М 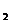
 , М
, М 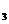
 , М
, М 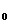
 .
.
2.Найти косинус угла между плоскостями 3х-2у+z=3 и x+2e+3z-29=0.
3.Найти точку пересечения плоскости  и прямой
и прямой  .
.
4.Найти проекцию точки А( 2; 3; 4) на прямую x=y=z.
«ЛИНИИ ВТОРОГО ПОРЯДКА»
«Эллипс»
Асимптоты гиперболы.
Определение 5. Прямая y=kx+m называется наклонной асимптотойкривой y = f(x) при х → +∞,если
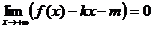 . (9)
. (9)
Аналогично определяется асимптота при х → –∞. Докажем, что прямые
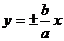 (10)
(10)
являются асимптотами гиперболы (4) при х → ±∞.
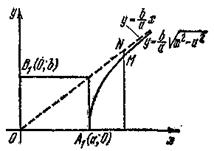
Рис. 3
Так как прямые (10) и гипербола (4) симметричны относительно координатных осей, то достаточно рассмотреть только те точки указанных линий, которые расположены в первой четверти (рис. 3). Напишем уравнения прямых (10) и гиперболы (4), соответствующие первой четверти:
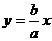 ,
,
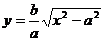 .
.
Положив 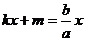 и
и 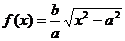 , найдем
, найдем
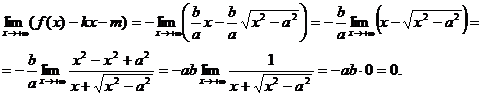
Следовательно, прямые (10) являются асимптотами гиперболы (4).
Отметим, что асимптоты (10) являются продолжениями диагоналей прямоугольника, стороны которого параллельны осям Ох и Оу и равны соответственно 2а и 2b, а его центр находится в начале координат.
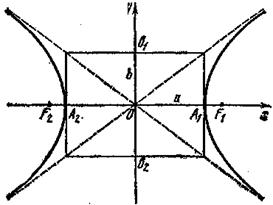
Рис. 4
При этом ветви гиперболы расположены внутри вертикальных углов, образуемых асимптотами, и приближаются сколь угодно близко к асимптотам (рис. 4).
Эксцентриситет гиперболы.
Определение 6. Эксцентриситетом гиперболыназывается отношение расстояния между фокусами к длине действительной оси и обозначается буквой ε:
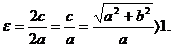 (11)
(11)
5. Сопряженная гипербола. Рассмотрим уравнение вида
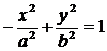 . (12)
. (12)
При переходе к новой системе координат, полученной в результате поворота осей старой системы вокруг начала координат на угол α = 90° (или α = –90°), уравнение (12) преобразуется в уравнение гиперболы
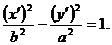
Следовательно, кривая, определяемая уравнением (12), есть гипербола, действительная ось 2b которой расположена на оси Оу, а мнимая ось 2а – на оси Ох.
Две гиперболы, которые определяются уравнениями
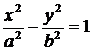 и
и 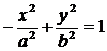
в одной и той же системе координат и при одних и тех же значениях а и b, называются сопряженнымидруг с другом.
Равносторонняя гипербола.
Определение 7. Гипербола называется равносторонней,если длины ее полуосей равны между собой, т.е. а=b. В этом случае уравнение гиперболы принимает вид
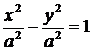 ,
,
или
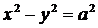 . (13)
. (13)
Равносторонняя гипербола определяется одним параметром а и асимптотами являются биссектрисы координатных углов
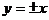 .
.
У всех равносторонних гипербол один и тот же эксцентриситет
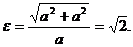
Так как асимптоты равносторонней гиперболы взаимно перпендикулярны, их можно принять за оси новой системы координат Ox'y', полученной в результате поворота осей старой системы вокруг начала координат на угол α = –45° (рис. 5). Составим уравнение равносторонней гиперболы относительно новой системы координат Ох'у'.
Учитывая равенство (13), получим x'y' = а2/2. (14)
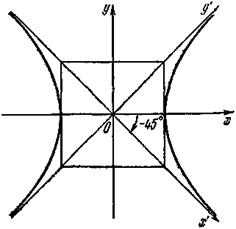
Рис. 5
Определение 8. Уравнение (14) называется уравнением равносторонней гиперболы, отнесенной к своим асимптотам.
Из уравнения (14) следует, что переменные х' и у' – величины обратно пропорциональные. Таким образом, равносторонняя гипербола, отнесенная к своим асимптотам, представляет собой график обратной пропорциональной зависимости.
Если центр гиперболы находится не в начале координат, а в точке О'(х0; у0), а оси гиперболы параллельны осям координат, то уравнение гиперболы будет иметь вид
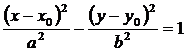
 или
или 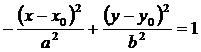 (15)
(15)
Это уравнения гиперболы со смещенным центром.
«Парабола»
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
№1. Составить уравнение окружности:
a. с центром в начале координат и радиусом 7;
b. с центром в точке (-1;4) и радиусом 2.
Построить данные окружности в прямоугольной декартовой системе координат.
№2. Составить каноническое уравнение эллипса с вершинами
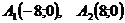 и фокусами
и фокусами 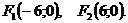
№3. Построить эллипс, заданный каноническим уравнением:
1) 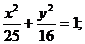 2)
2) 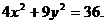
№4. Составить каноническое уравнение эллипса с вершинами
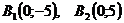 и фокусами
и фокусами 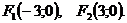
№5. Составить каноническое уравнение гиперболы с вершинами
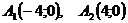 и фокусами
и фокусами 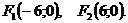
№6. Составить каноническое уравнение гиперболы, если:
1. расстояние между фокусами 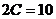 , а между вершинами
, а между вершинами 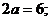
2. действительная полуось 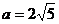 , а эксцентриситет
, а эксцентриситет 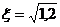 ;
;
3. фокусы на оси 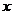 , действительная ось 12, а мнимая 8.
, действительная ось 12, а мнимая 8.
№7. Построить гиперболу, заданную каноническим уравнением:
1) 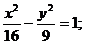 2)
2) 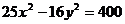 .
.
№8. Составить каноническое уравнение параболы, если:
1) парабола расположена в правой полуплоскости симметрично относительно оси 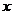 и её параметр
и её параметр 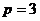 ;
;
2) парабола расположена в левой полуплоскости симметрично относительно оси и её параметр 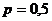 .
.
Построить эти параболы, их фокусы и директрисы.
№9. Определить тип линии, если её уравнение:
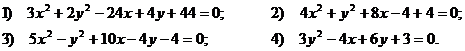
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Векторы в пространстве.
1.1. Что такое вектор?
1.2. Что такое абсолютная величина вектора?
1.3. Какие виды векторов в пространстве Вы знаете?
1.4. Какие действия можно выполнять с ними?
1.5. Что такое координаты вектора? Как их найти?
2. Действия над векторами, заданными своими координатами.
2.1. Какие действия можно выполнять с векторами, заданными в координатной форме (правила, равенства, примеры); как найти абсолютную величину такого вектора.
2.2. Свойства:
2.2.1 коллинеарных;
2.2.2 перпендикулярных;
2.2.3 компланарных;
2.2.4 равных векторов.
(формулировки, равенства).
3. Уравнение прямой. Прикладные задачи.
3.1. Какие виды уравнения прямой Вы знаете (уметь записывать и интерпретировать по записи);
3.2. Как исследовать на параллельность – перпендикулярность две прямые, заданные уравнениями с угловым коэффициентом или общими уравнениями?
3.3. Как найти расстояние от точки до прямой, между двумя точками?
3.4. Как найти угол между прямыми, заданными общими уравнениями прямой или уравнениями с угловым коэффициентом?
3.5. Как найти координаты середины отрезка и длину этого отрезка?
4. Уравнение плоскости. Прикладные задачи.
4.1. Какие виды уравнения плоскости Вы знаете (уметь записывать и интерпретировать по записи)?
4.2. Как исследовать на параллельность – перпендикулярность прямые в пространстве?
4.3. Как найти расстояние от точки до плоскости и угол между плоскостям?.
4.4. Как исследовать взаимное расположение прямой и плоскости в пространстве?
4.5. Виды уравнения прямой в пространстве: общее, каноническое, параметрическое, проходящей через две данные точки.
4.6. Как найти угол между прямыми и расстояние между точками в пространстве?
5. Линии второго порядка.
5.1. Эллипс: определение, фокусы, вершины, большая и малая оси, фокальные радиусы, эксцентриситет, уравнения директрис, простейшие (или канонические) уравнения эллипса; чертеж.
5.2. Гипербола: определение, фокусы, вершины, действительная и мнимая оси, фокальные радиусы, эксцентриситет, уравнения директрис, простейшие (или канонические) уравнения гиперболы; чертеж.
5.3. Парабола: определение, фокус, директриса, вершина, параметр, ось симметрии, простейшие (или канонические) уравнения параболы; чертеж.
Примечание к 4.1, 4.2, 4.3: Для каждой линии 2го порядка уметь описывать построение.
ЗАДАНИЯ ДЛЯ САМОПРОВЕРКИ
1.Даны точки: 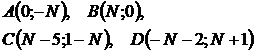 , где N – номер студента по списку.
, где N – номер студента по списку.
1. Найти координаты, абсолютные величины и направляющие косинусы векторов 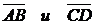 .
.
2. При каком значении числа 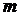 перпендикулярны векторы
перпендикулярны векторы 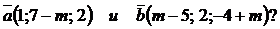
3. Проверить, коллинеарны ли векторы 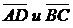 ?
?
4. Образуют ли векторы 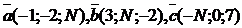 базис?
базис?
5. Найти угол между векторами 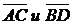 .
.
6. Образуют ли векторы 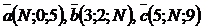 базис? Если да, найти в нем координаты вектора
базис? Если да, найти в нем координаты вектора 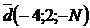 .
.
2.Даны координаты вершин треугольника A, B, C (сделать чертеж). Найти:
1) уравнение стороны AB;
2) уравнение медианы AF;
3) уравнение высоты CK;
4) длины сторон треугольника и высоты CK;
5) косинус угла ABC.
1. A (-3; 2), B (0; 14), C (6; 6).
2. A (-3; -1), B (0; 13), C (6; 5).
3. A (6; 2), B (9; 14), C (15; 6).
4. A (-1; -1), B (2; 11), C (8; 3).
5. A (11; -2), B (10; 10), C (16; 2).
3. Даны четыре точки М 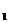
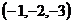 , М
, М 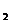
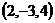 , М
, М 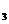
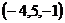 , М
, М 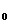
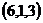 . Требуется:
. Требуется:
1) написать уравнение плоскости Р, проходящей через точки М 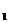 , М
, М 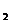 , М
, М 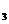 ;
;
2) преобразовать полученное уравнение плоскости Р в уравнение плоскости в отрезках и построить эту плоскость;
3) найти расстояние от точки М 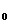 до плоскости Р.
до плоскости Р.
4. Построить линию второго порядка, заданную своим каноническим уравнением:
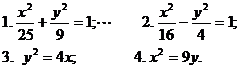 .
.
ЛИТЕРАТУРА
1.Высшая математика для экономистов - Учебник для вузов под ред. Н.Ш. Кремер и д
