Теорема о сложении скоростей для сложного

движения точки.

Теорема. Скорость абсолютного движения точки равна

векторной сумме переносной и относительной скоростей.

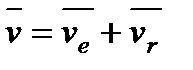
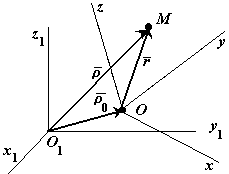
Доказательство. Рассмотрим движение точки М.

Положение точки М относительно неподвижной системы

отсчета определяется вектором 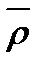, а относительно

подвижной вектором 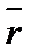. Положение точки О относительно

неподвижной системы отсчета определяется вектором .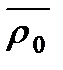

Для любого момента времени выполняется тождество .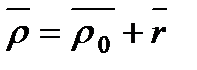

Продифференцируем его по времени (вычислим производные

в неподвижной системе отсчета) и получим

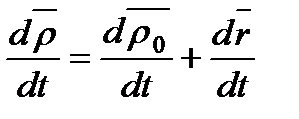(1) По определению, 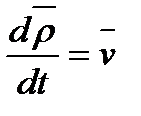- абсолютная скорость точки

М, 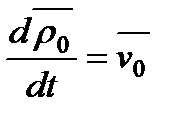- абсолютная скорость точки О. Для вычисления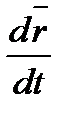

применим формулу Бура. Имеем 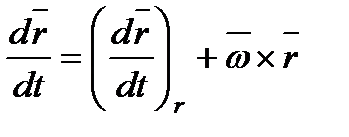. Относительная

производная 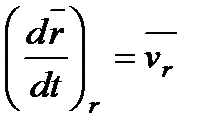- является относительной скоростью точки М

по отношению к неподвижной системе отсчета, а -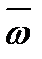

угловая скорость вращения подвижной системы отсчета.

Таким образом из (1) получаем

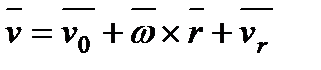(2) Скорость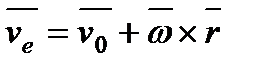

является скоростью точки свободного твердого тела,

скрепленного с подвижной системой координат, с

которой в данный момент совпадает точка М в движении

тела относительно неподвижной системы отсчета. Это

есть переносная скорость точкиМ. Окончательно получаем

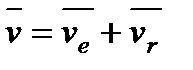, (3) что и требовалось доказать.

Теорема Кориолиса о сложении Ускорений.

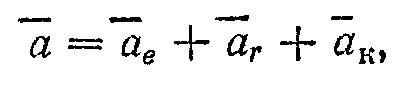
Модуль и направление кориолисова

ускорения. Различные случаи определения

Направления кориолисова ускорения.

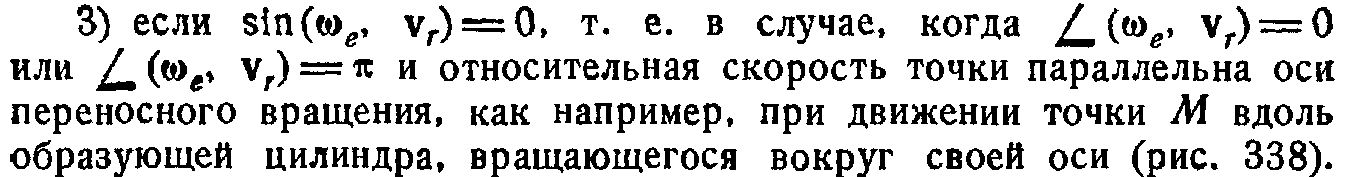
Сложение поступательного и

Вращательного движений. Винтовое движение.

Если сложное движение тела слагается из

вращательного вокруг оси Аа с угловой скоростью

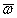и поступательного со скоростью 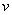, направленной

параллельно оси Аа (рис.63), то такое движение тела

называется винтовым. Ось Аа называют осью винта.

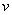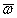Когда векторы и направлены в одну сторону,

то при принятом нами правиле изображения 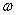винт

будет правым; если в разные стороны, - левым.

Расстояние, проходимое за время одного оборота

любой точкой тела, лежащей на оси винта, называется

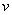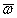шагом h винта. Если величи­ны и постоянны, то

шаг винта также будет постоянным. Обо­значая время

одного оборота через Т, получаем в этом случае 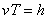и

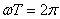, откуда .

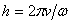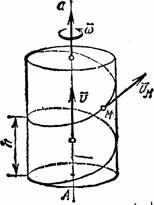Рис.63

При постоянном шаге любая точка М тела, не

лежащая на оси винта, описывает винтовую линию.

Скорость точки М, находящей­ся от оси винта на

расстоянии 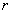, слагается из поступательной ско­рости

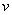и перпендикулярной ей скорости, получаемой во

враща­тельном движении, которая численно равна .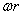

Следовательно, 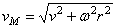.Направлена скорость 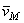по

касательной к винтовой линии. Если цилиндрическую

поверхность, по которой движется точка М, разрезать

вдоль образующей и развернуть, то винтовые линии,

обратятся в прямые, наклоненные к основанию цилиндра

под углом .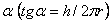

Сложение вращательных движений т.т. вокруг

Пересекающихся осей. Модуль и направление угловой

Скорости и углового ускорения в суммирующем вращении.