Плоскопараллельное движение т.т.

Плоскопараллельное движение т.т.

Уравнение плоскопараллельного

Движения.

Плоско-параллельным или плоским

движением твердого тела называется

такое движение,

при котором все точки

тела движутся в плоскостях,

параллельных некоторой

неподвижной плоскости.

Теорема о перемещениях плоской

фигуры

Теорема. Перемещение плоской

фигуры в ее плоскостиможно

осуществить путем поступательного

перемещения вместе с произвольно

выбранным полюсом и вращения

вокруг полюса. При этом угол

поворота от выбора полюса не зависит.

Пусть плоская фигура

движется внеподвижной

плоскости. Выберем в

качестве полюса точку

А плоской фигуры и

свяжем с ней подвижную систему

координат, движущуюся вместе с фигурой.

Для определения положенияподвижной

системы координат относительно

неподвижнойследует задать положение

полюса А и угол поворота ϕ вокруг полюс

Координаты любой точки М будут:

Теорема о скоростях точек плоской

Фигуры. Мгновенный центр(ц.с.) скоростей

Т-ма об ускорениях точек плоской фигуры.

Мгновенный центр ускорений (М.Ц.У.). Различ.

случаи определения положения М.Ц.У.

Теорема: Ускорение любой точки плоской фигуры

определяется как геометрическая сумма ускорения

полюса и ускорения этой точки во вращении вокруг

полюса

Если мгновенный центр ускорений принять за

полюс, то ускорение любой точки плоской фигуры

в данный момент определится как ускорение этой

точки во вращательном движении вокруг центра

ускорений.

Модули ускорений точек плоской фигуры в

каждый момент времени пропорциональны рас­

стояниям этих точек до мгновенного центра уско­

рений. Углы, которые составляют эти ускорения с

лучами, проведенными в мгновенный центр уско­

рений, одинаковы для всех точек. Мгновенный

центр ускорений и мгновенный центр скоростей -

разные точки.

Определения положения М.Ц.У.

1.Пусть известны направления ускорений двух

точек плоской фигуры, ее угловые скорость и

ускорение. Тогда МЦУ лежит на пересечении

прямых линий, проведенных к векторам ускорений

точек фигуры под одним и тем же острым углом: ,

отложенным от векторов ускорений точек в

направлении дуговой стрелки углового ускорения.

2. Пусть известны направления ускорений хотя бы

двух точек плоской фигуры, ее угловое ускорение = 0,

а угловая скорость не равна 0.

3. Угловая скорость= 0, угловое ускорение не равно 0.

Угол прямой.

Относительное, переносное и абсолютное

Движение точки.

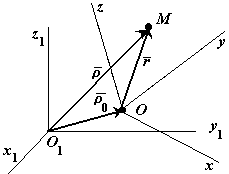
Пусть система отсчета O₁x₁y₁z₁ - неподвижная,

а система отсчета Oxyz - подвижная. Движение

точки относительно основной неподвижной

системы отсчета O₁x₁y₁z₁ называется

абсолютным. Движение точки

относительно подвижной системы

отсчета Oxyz называется относительным.

Переносным движением точки называется

движение, которое она совершает вместе с

подвижной системой отсчета, как точка, жестко

скрепленная с этой системой в рассматриваемый

момент времени.Относительные скорость и

ускорение обозначают и , переносные–

и , а абсолютные - и .

Движение подвижной системы отсчета относительно

неподвижной можно охарактеризовать скоростью ее

поступательного движения , например вместе с

точкойО, и вектором угловой скорости ее вращения

вокруг О. системе отсчёта называется сложным или

абсолютным, а скорость и ускорение этого движения —

абсолютной скоростью va и абсолютным ускорением wa.

Сложение поступательного и

Плоскопараллельное движение т.т.