Дифференциал функции. определение, свойства.

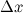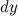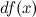Дифференциалом функции называется линейная относительно часть приращения функции. Она обозначается как или . Таким образом:

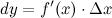
Дифференциал независимой переменной равен ее приращению:
dx=Δx

Дифференциал функции равен произведению производной на дифференциал независимой переменной:
dy=df(x)=f′(x)dx

Выражение производной через дифференциалы
f′(x)=dydx

Дифференциал постоянного числа равен нулю:
dC=0

Дифференциал суммы функций равен сумме дифференциалов:
d(u+v)=du+dv

Дифференциал разности функций равен разности дифференциалов:
d(u−v)=du−dv

Постоянный множитель можно выносить за знак дифференциала:
d(Cu)=Cdu

Дифференциал произведения функций
d(uv)=vdu+udv

Дифференциал частного
d(uv)=vdu−udvv2

ПЕРВООБРАЗНАЯ, ТЕОРЕМА ОБ ОБЩЕМ ВИДЕ ПЕРВООБРАЗНЫХ К ДАННОЙ ФУНКЦИИ (ВЫВОД). ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ПЕРВООБРАЗНОЙ.

(Об общем виде первообразной для функции)

9. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ОПРЕДЕЛЕНИЕ, ОСНОВНЫЕ СВОЙСТВА.

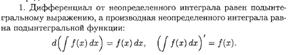
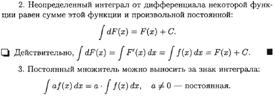
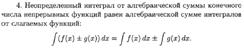
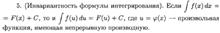
ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ

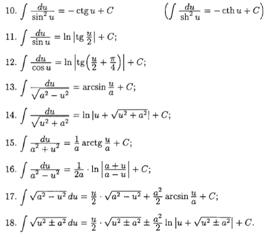
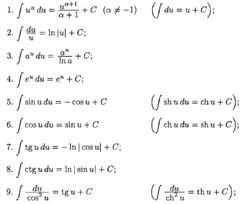
ФОРМУЛА ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ

Метод вычисления интегралов, называемый интегрированием по частям, основан на правиле дифференцирования произведения.

Пусть

u=u(x), v=v(x)u=u(x), v=v(x)

— функции, дифференцируемые на некотором промежутке Х.Тогда, как известно, дифференциал произведения этих функций вычисляется по формулеd(uv)=udv+vdu.

Взяв неопределенный интеграл от обеих частей этого равенства, получим

∫d(uv)=∫(udv+vdu) т.к. ∫d(uv)=uv+C , а ∫(udv+vdu)=∫udv+∫vdu

то получаем: uv+C=∫udv+∫vduоткуда ∫udv=uv+C−∫vdu

Поскольку ∫vdu∫vdu уже содержит произвольную постоянную, в правой части полученного равенства C можно опустить и записать равенство в виде ∫udv=uv−∫vdu

предположили, что функции u(x)u(x) и v(x)v(x)дифференцируемы

ОПРЕДЕЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ (ВЫВОД). ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ИНТЕГРАЛА.

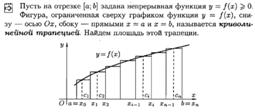
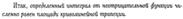
ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.

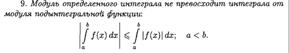
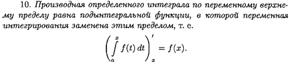
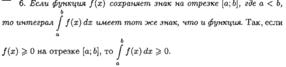
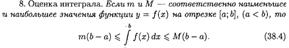
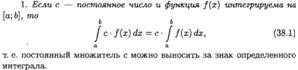
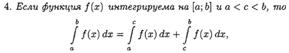
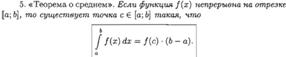
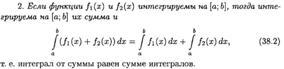
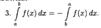
ТЕОРЕМА О СРЕДНЕМ ЗНАЧЕНИИ (ВЫВОД, ГЕОМЕТРИЧЕСКИЙ СМЫСЛ). ЧТО НАЗЫВАЕТСЯ СРЕДНИМ ЗНАЧЕНИЕМ ФУНКЦИИ НА ОТРЕЗКЕ?

ПРОИЗВОДНАЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПО ВЕРХНЕМУ ПРЕДЕЛУ (ВЫВОД).

16. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА

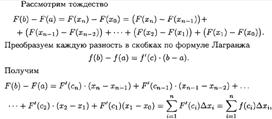
17. ФОРМУЛА ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ ДЛЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.

18. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

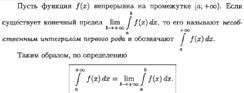
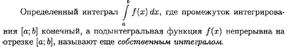
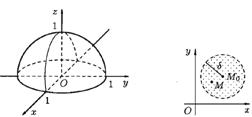
19. ОПРЕДЕЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. ГРАФИК ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ.

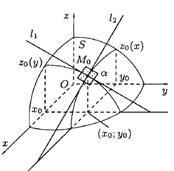
ЧАСТНЫЕ ПРОИЗВОДНЫЕ ПЕРВОГО ПОРЯДКА (ОПРЕДЕЛЕНИЕ, ГЕОМЕТРИЧЕСКИЙ СМЫСЛ). ЧАСТНЫЕ ПРОИЗВОДНЫЕ ВТОРОГО ПОРЯДКА. ТЕОРЕМА ШВАРЦА.

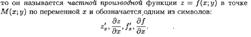
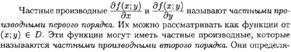
21. ПОЛНОЕ ПРИРАЩЕНИЕ И ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ, СВЯЗЬ МЕЖДУ НИМИ.

24. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА.

КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ.