Расчёт разрезной балки на изгиб

Рассматриваемый метод решения задач сопротивления материалов охватывает также случай составного стержня, отдельные части которого связаны между собой внутренними связями типа шарнирного соединения, подвижной заделки и т. п. Порядок решения данного типа задач проиллюстрируем на примере разрезной постоянной жёсткости балки, работающей на изгиб (рис. 5.3).

Рис. 5.3. Изгиб разрезной балки постоянной жёсткости

Изгиб сплошной балки в плоскости 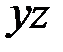описывается системой уравнений (2.59). Если балка содержит один или несколько врезанных шарниров, то нужно внести изменение в третье уравнение (2.59), записав его в виде

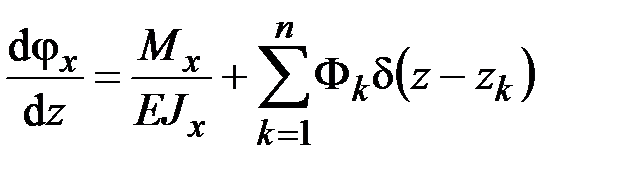. (5.8)

Здесь 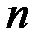– число врезанных шарниров;

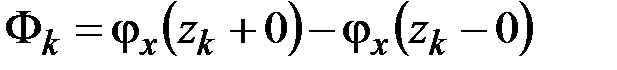(5.9)

– скачок угла поворота поперечного сечения балки при переходе через врезанный шарнир, положение которого (в недеформированном состоянии) определяется координатой 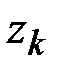. При решении задачи величины (5.9) заранее неизвестны, их численное значение определяется с помощью дополнительных ограничивающих условий

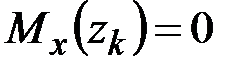
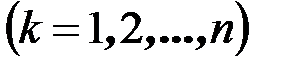, (5.10)

накладываемых на изгибающий момент в сечениях .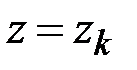

В рассматриваемой задаче (рис. 5.3) изгиб разрезной балки с врезанным шарниром 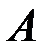описывается системой уравнений

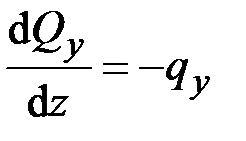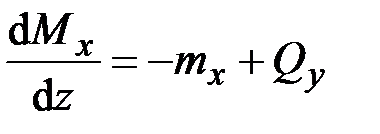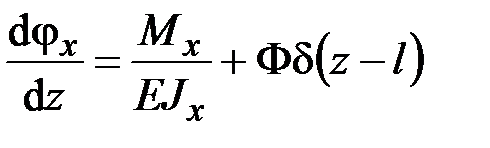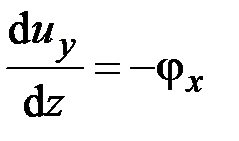, , , . (5.11)

Внешние погонные нагрузки равны

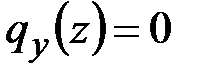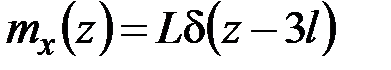, . (5.12)

Кинематические и силовые граничные условия имеют вид

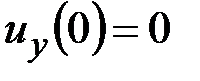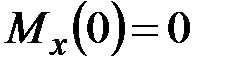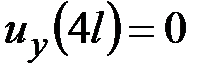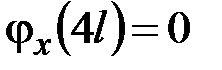, , , . (5.13)

К ним нужно добавить ограничение

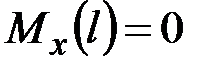. (5.14)

Пяти соотношений (5.13), (5.14) достаточно, чтобы определить пять неизвестных величин , , , , .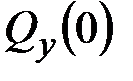

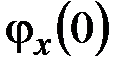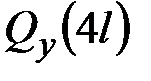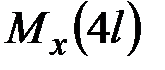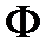Проинтегрируем первые два уравнения (5.11) с учётом (5.12), (5.13). В результате получим

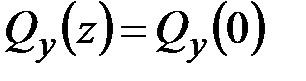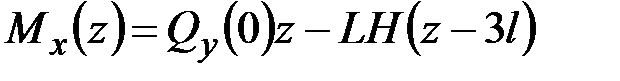, . (5.15)

Отсюда на основании (5.14) имеем

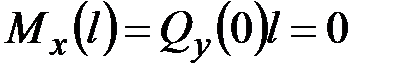
или

.

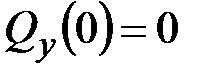Это позволяет переписать (5.15) в виде

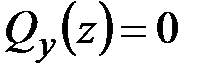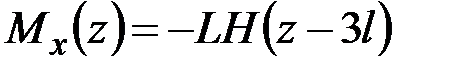, . (5.16)

Подставим (5.16) в третье уравнение (5.11) и проведём интегрирование:

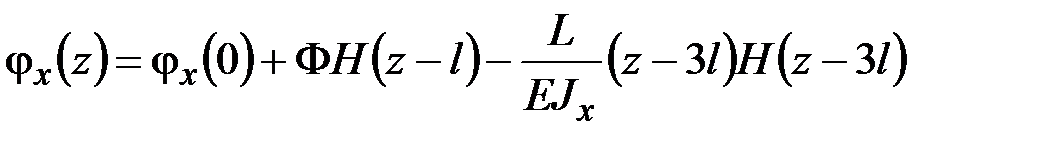. (5.17)

В свою очередь, подстановка (5.17) в последнее уравнение (5.11) и последующее интегрирование с учётом (5.13) даёт следующий результат:

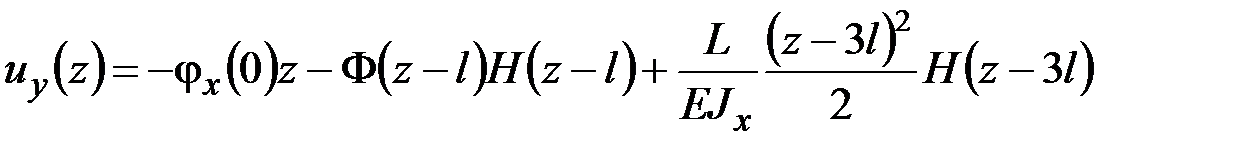. (5.18)

Наконец, воспользуемся двумя последними граничными условиями (5.13). На основании (5.17), (5.18) будем иметь

, .

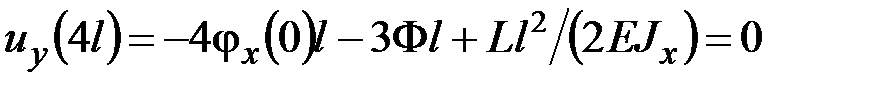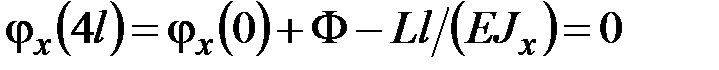Решая систему алгебраических уравнений

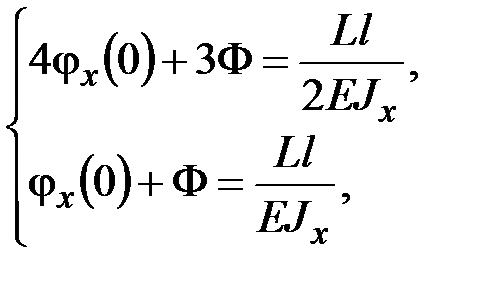
находим

, .

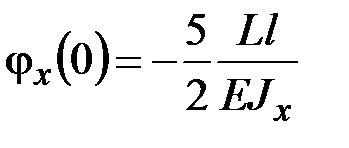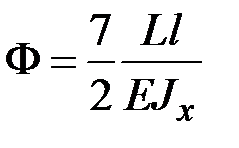Таким образом, задача решена полностью.

Контрольные вопросы

1. Заполните таблицу для геометрических характеристик плоского сечения 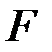, выбирая обозначения и расчётные формулы из следующих двух списков:

{ , , , , , , }

{ , , , , , , }

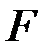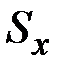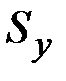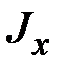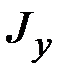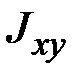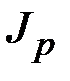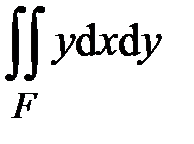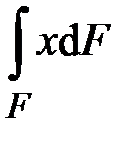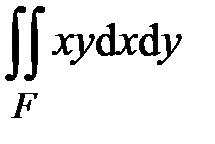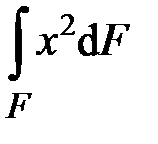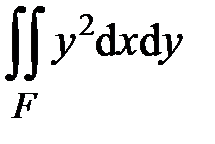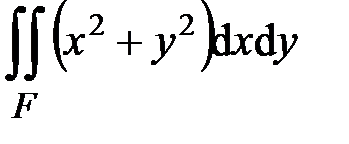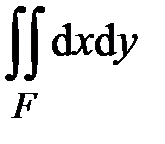Геометрическая характеристика	Обозначение	Расчётная формула
Статический момент относительно оси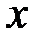
Площадь сечения
Центробежный момент инерции
Полярный момент инерции
Осевой момент инерции относительно оси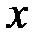
Статический момент относительно оси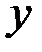

2. Для плоского сечения 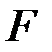оси 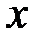, 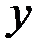являются

· центральными осями, если

· главными осями, если

3. Чему равен полярный момент сопротивления сечения?

· · ·

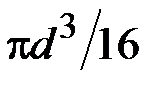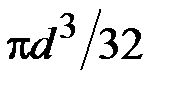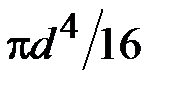4. Чему равен осевой момент инерции сечения относительно центральной оси ?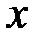

	· · ·
	· · ·

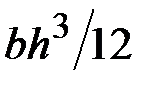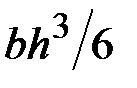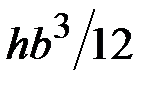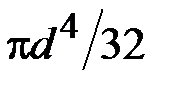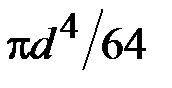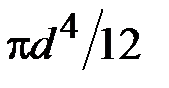5. Чему равен момент сопротивления сечения относительно центральной оси ?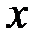

· · ·

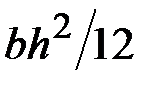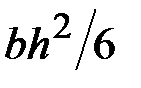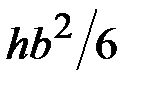6. В нагруженном теле внутренняя сила, приходящаяся на единицу площади какого-либо сечения, называется ______________ в данной точке на данной площадке.

· продольной силой

· поперечной силой

· напряжением

· критической силой

· сосредоточенной силой

7. Как называется проекция вектора полного напряжения на плоскость сечения?

· нормальное напряжение

· касательное напряжение

· главное напряжение

8. Как называется проекция вектора полного напряжения на нормаль сечения?

· нормальное напряжение

· касательное напряжение

· главное напряжение

9. Что такое главная площадка напряжений?

· площадка, на которой отсутствуют нормальные напряжения

· площадка, на которой нормальные и касательные напряжения между собой равны

· площадка, на которой отсутствуют касательные напряжения

10. Впишите номер вектора, соответствующего указанным напряжениям:

· – _______ · – _______ · – _______

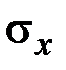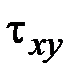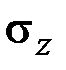11. Какие выражения соответствуют закону парности касательных напряжений?

·

·

·

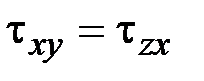
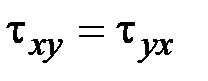
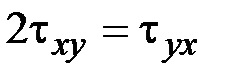
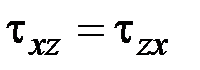
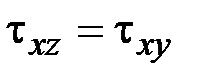
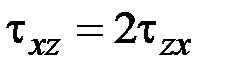
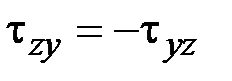
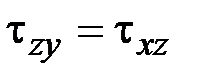
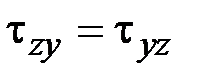
12. Каков физический смысл модуля Юнга?

· коэффициент пропорциональности между поперечной и продольной деформацией

· коэффициент пропорциональности между нормальным напряжением и линейной деформацией

· коэффициент пропорциональности между касательным напряжением и угловой деформацией

13. Каков физический смысл модуля сдвига?

· коэффициент пропорциональности между поперечной и продольной деформацией

· коэффициент пропорциональности между нормальным напряжением и линейной деформацией

· коэффициент пропорциональности между касательным напряжением и угловой деформацией

14. Заполните таблицу для внутренних усилий в поперечном сечении 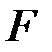, выбирая обозначения и расчётные формулы из следующих двух списков:

{ , , , , , }

{ , , , , , , , , }

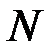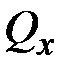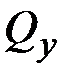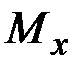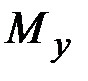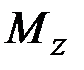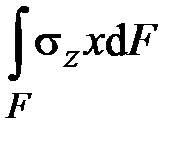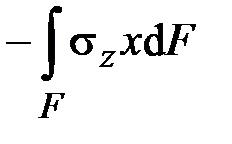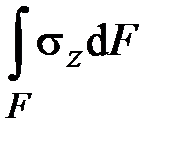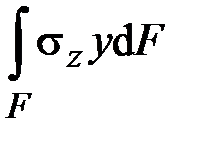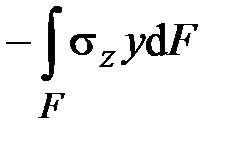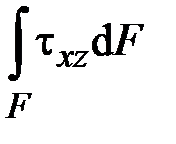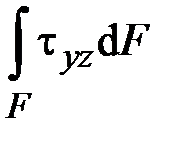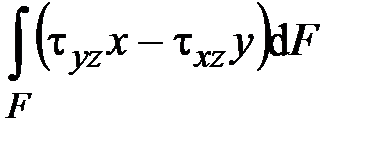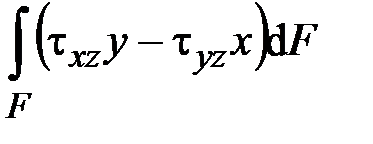Внутреннее усилие	Обозначение	Расчётная формула
Поперечная сила по оси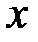
Поперечная сила по оси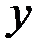
Продольная сила
Крутящий момент
Изгибающий момент в плоскости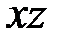
Изгибающий момент в плоскости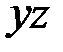

15. Данная система дифференциальных уравнений

,

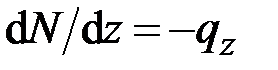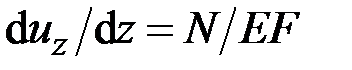
описывает

· растяжение-сжатие прямого стержня

· изгиб прямого стержня в плоскости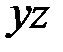

· кручение прямого стержня

16. Данная система дифференциальных уравнений

,

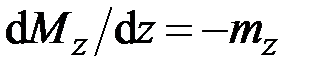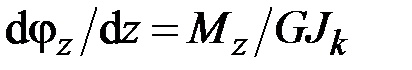
описывает

· растяжение-сжатие прямого стержня

· изгиб прямого стержня в плоскости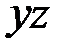

· кручение прямого стержня

17. Данная система дифференциальных уравнений

, , ,

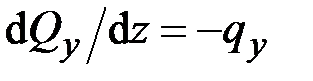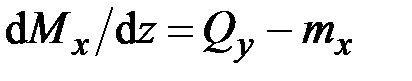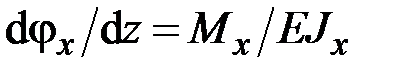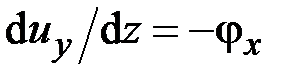
описывает

· растяжение-сжатие прямого стержня

· изгиб прямого стержня в плоскости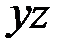

· кручение прямого стержня

18. Запишите систему дифференциальных уравнений, моделирующих растяжение-сжатие прямого стержня:

19. Запишите систему дифференциальных уравнений, моделирующих кручение прямого стержня:

20. Запишите систему дифференциальных уравнений, моделирующих изгиб прямого стержня в плоскости :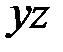

21. Укажите правильный вариант записи силового граничного условия. Для выбранного варианта впишите кинематические граничные ус­ловия.

· , _______________________________________________

· , ______________________________________________

· , ________________________________________________

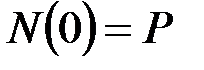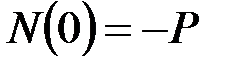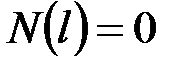22. Укажите правильный вариант записи силового граничного ус­ловия. Для выбранного варианта впишите кинематические граничные условия.

· , _______________________________________________

· , ______________________________________________

· , _______________________________________________

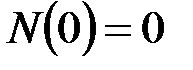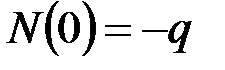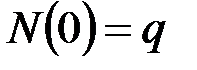23. Укажите правильный вариант записи силового граничного ус­ловия. Для выбранного варианта впишите кинематические граничные условия.

· , _____________________________________________

· , _______________________________________________

· , _______________________________________________

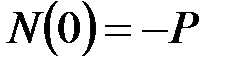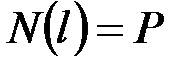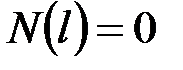24. Укажите правильный вариант записи силового граничного ус­ловия. Для выбранного варианта впишите кинематические граничные условия.

· , ______________________________________________

· , _______________________________________________

· , _______________________________________________

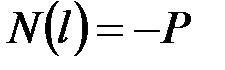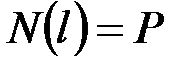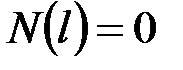25. Укажите правильный вариант записи силового граничного ус­ловия. Для выбранного варианта впишите кинематические граничные условия.

· , , ____________________________________

· , , _____________________________________

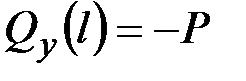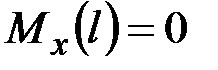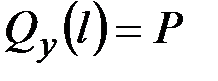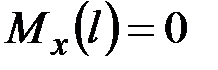26. Укажите правильный вариант записи силового граничного ус­ловия. Для выбранного варианта впишите кинематические граничные условия.

· , , ______________________________________

· , , ____________________________________

· , , _____________________________________

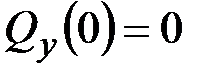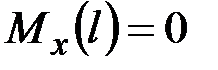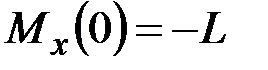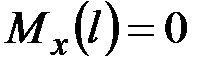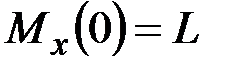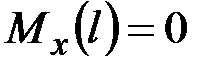27. Укажите правильный вариант записи силового граничного ус­ловия. Для выбранного варианта впишите кинематические граничные условия.

· , , ____________________________________

· , , ____________________________________

· , , _____________________________________

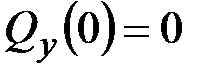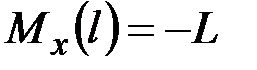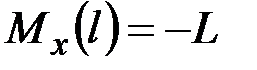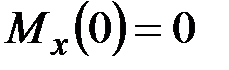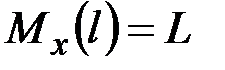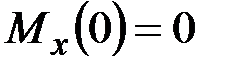28. Укажите правильный вариант записи силового граничного ус­ловия. Для выбранного варианта впишите кинематические граничные условия.

· , , ____________________________________

· , , ____________________________________

· , , ___________________________________

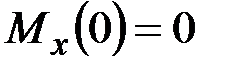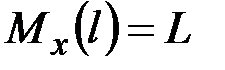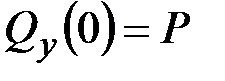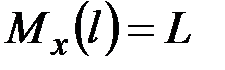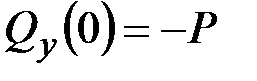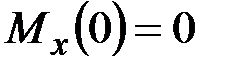29. Укажите правильный вариант записи силового граничного ус­ловия. Для выбранного варианта впишите кинематические граничные условия.

· , ______________________________________________

· , ______________________________________________

· , ____________________________________________

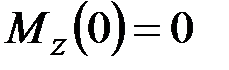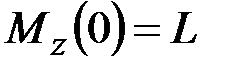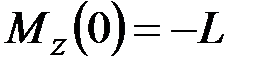30. Укажите правильный вариант записи силового граничного ус­ловия. Для выбранного варианта впишите кинематические граничные условия.

· , _____________________________________________

· , ______________________________________________

· , ______________________________________________

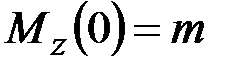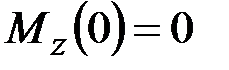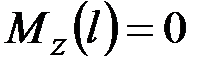31. Способность конструкций и деталей машин выдерживать рабочие нагрузки без разрушения и пластических деформаций называется

· прочностью

· жесткостью

· устойчивостью

32. Способность конструкций и деталей машин выдерживать рабочие нагрузки без значительных упругих деформаций, которые могут нарушить их нормальную работу, называется

· прочностью

· жесткостью

· устойчивостью

33. Способность конструкции и её элементов сохранять определенную начальную форму упругого равновесия под нагрузкой называется

· прочностью

· жесткостью

· устойчивостью

34. Способность материальных тел восстанавливать первоначальную форму и размеры после снятия нагрузки называется

· упругостью

· пластичностью

· материальной однородностью

· изотропностью

35. Способность материальных тел не восстанавливать первоначальную форму и размеры после снятия нагрузки называется

· упругостью

· пластичностью

· материальной однородностью

· изотропностью

36. Способность материала проявлять одинаковые свойства во всех точках называется

· упругостью

· пластичностью

· материальной однородностью

· изотропностью

37. Способность материала проявлять одинаковые свойства во всех направлениях называется

· упругостью

· пластичностью

· материальной однородностью

· изотропностью

38. Чему равны крутящие моменты в сечениях бруса 1 – 1 и 2 – 2?

· , · , · , · ,

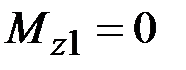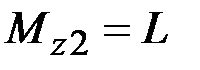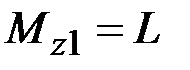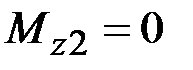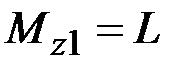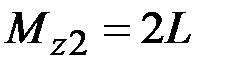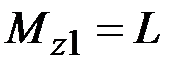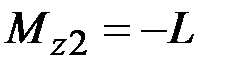39. Как соотносятся между собой крутящие моменты в сечениях бруса 1 – 1 и 2 – 2?

· · ·

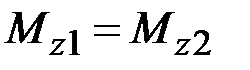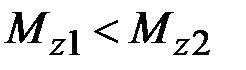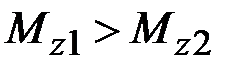40. В какой из точек возникнут наибольшие по модулю нормальные напряжения?

· А · В · С

41. Определите абсолютное удлинение ступенчатого стержня.

· · ·

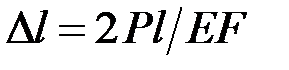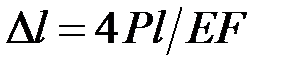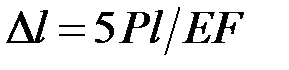42. Как изменится напряжение в точке D, если убрать силу Р, параллельную оси ?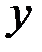

· увеличится в два раза · уменьшится в два раза · изменится знак · уменьшится в три раза · не изменится

43. Определите абсолютное удлинение ступенчатого стержня.

· · ·

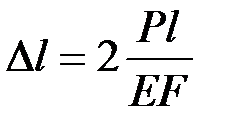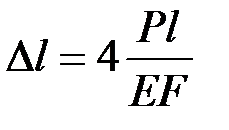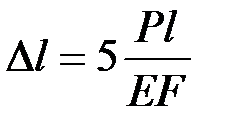44. Чему равны (по модулю) изгибающие моменты в сечениях А, В, С, D? (Сечения В и С находятся на ничтожно малых расстояниях от сечения, где приложена сила Р).

· , , · , , · , , · ,

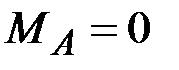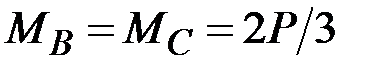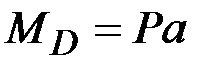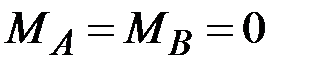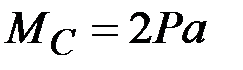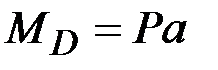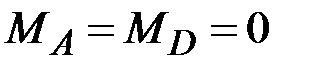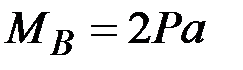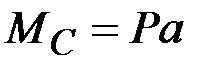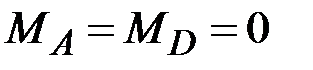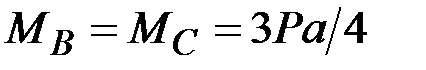45. Чему равны (по модулю) изгибающие моменты в сечениях А, В, С, D? (Сечения В и С находятся на ничтожно малых расстояниях от сечения, где приложен момент L).

· , , · , , · , , · ,

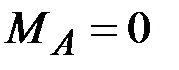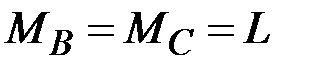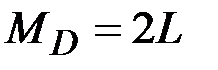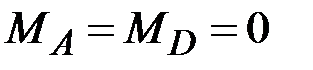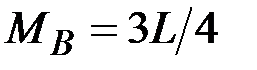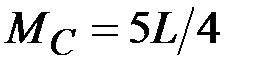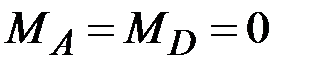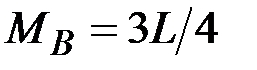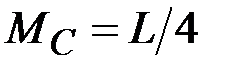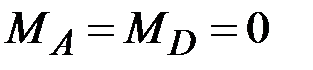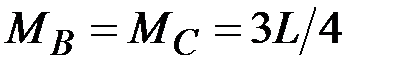46. Стержневая система состоит из круглого бруса диаметром d, длиной l и перпендикулярного к нему стержня АВС. На концах стержня АВС приложены силы Р, причём АВ = ВС = 2l. Момент сопротивления поперечного сечения бруса при кручении 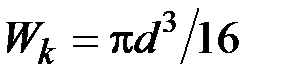, а при изгибе 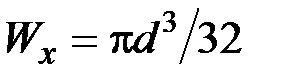. Как изменится наибольшее расчетное напряжение 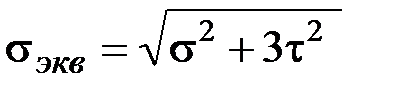в опасном сечении бруса, если убрать одну из сил?

· уменьшится в четыре раза · не изменится · уменьшится в два раза · увеличится в два раза · уменьшится в полтора раза

47. Укажите на формулу расчёта размера b квадратного поперечного сечения балки, исходя из условия прочности.

· · ·

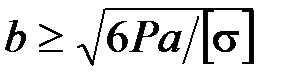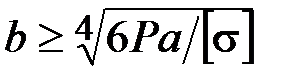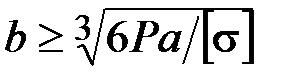48. Стержень подвергается изгибу с растяжением силами Р. Момент сопротивления круглого сечения при изгибе равен 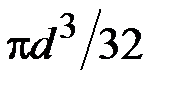. При каком значении сил Р достигается предельное напряжённое состояние?

· · · ·

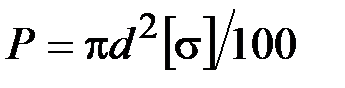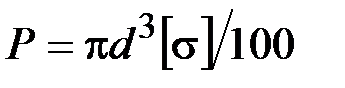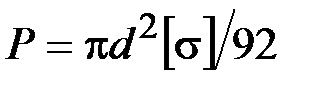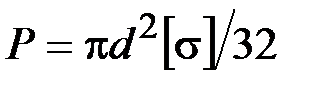49. Один конец бруса диаметра d и длины l жестко закреплен, а другой конец нагружен вертикальной и горизонтальной силами, а также скручивающим моментом М = 10Pl. Момент сопротивления поперечного сечения бруса при кручении 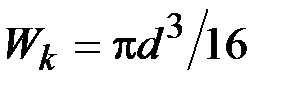, а при изгибе 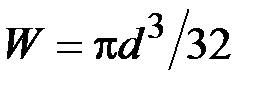. Используя энергетическую гипотезу прочности, по которой 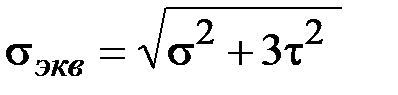, определить наибольшее допустимое значение силы P.

· · · ·

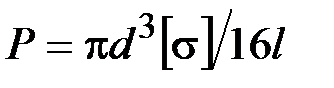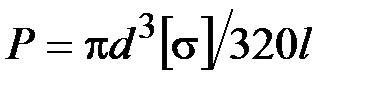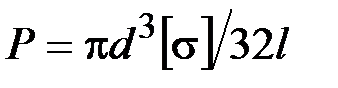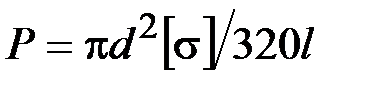Задачи для самостоятельного решения

Задача 1

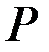Вертикально расположенный ступенчатый брус нагружен на свободном конце растягивающей силой . Найти распределение продольной силы, нормального напряжения и осевого перемещения по длине бруса. Заданы площадь 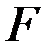, длина , удельный вес 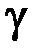, модуль Юнга .

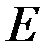Задача 2

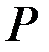Вертикально расположенный ступенчатый брус нагружен на свободном конце сжимающей силой . Найти распределение продольной силы, нормального напряжения и осевого перемещения по длине бруса. Известны площадь 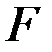, длина , удельный вес 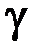, модуль Юнга .

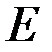Задача 3

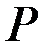Консольный кран несёт нагрузку . Определить внутренние усилия и перемещения балки 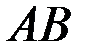, считая тягу 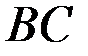нерастяжимой. Принять для балки 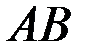площадь и момент инерции поперечного сечения равными 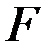, ; модуль Юнга – 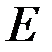. Геометрические размеры указаны на рисунке.

Задача 4

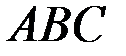К шарнирно опёртой разрезной балке приложена распределённая нагрузка интенсивностью 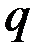. Считая известными размеры 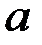и , модуль Юнга 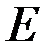и момент инерции поперечного сечения , определить внутренние усилия и перемещения балки.

Задача 5

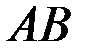На свободном конце защемлённой балки шарнирно закреплён блок, через который перекинут трос для поднятия груза 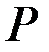. Определить силу натяжения 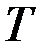, внутренние усилия и перемещения балки, считая известными длину , угол 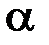, модуль Юнга 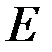, площадь 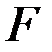и момент инерции поперечного сечения балки.

Задача 6

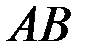На середине лестницы , установленной под углом 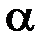, находится человек весом 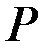. Считая лестницу балкой с поперечным сечением площадью 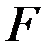, моментом инерции , длиной 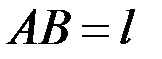и модулем Юнга 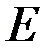, определить внутренние усилия и перемещения. Силами трения пренебречь.

Задача 7

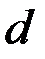На круглый вал диаметром насажены два колеса диаметром 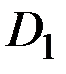и 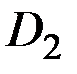, на которые действуют вес груза 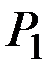и уравновешивающая сила 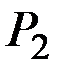, как показано на рисунке. Определить величину силы 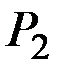, внутренние усилия и перемещения вала, полагая известными вес 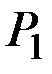, модуль Юнга 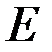, модуль сдвига 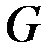и длину .

Задача 8

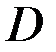Два шкива одинакового диаметра насажены на круглый вал диаметром 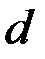и передают мощность 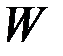при постоянной скорости вращения . Натяжение ведущего ремня вдвое больше натяжения ведомого ремня: 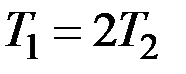. Определить силы натяжения, внутренние усилия и перемещения вала, полагая известными модуль Юнга 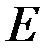, модуль сдвига 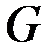и длину .

Задача 9

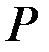Определить внутренние усилия и перемещения прямого бруса, нагруженного вертикальной и горизонтальной силами одинаковой величины , перпендикулярными оси бруса. Поперечное сечение бруса – квадрат со стороной 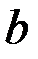, модуль Юнга – .

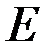Задача 10

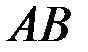Определить внутренние усилия и перемещения на участке консольного пространственного бруса 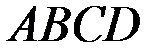круглого сечения диаметром 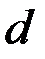, нагруженного горизон­тальной силой 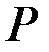. Модуль Юнга равен 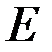, геометрические размеры: , .

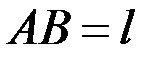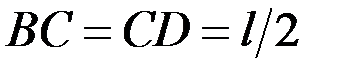Задача 11

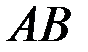Определить внутренние усилия и перемещения на участке консольного пространственного бруса 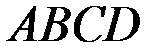круглого сечения диаметром 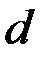, нагруженного горизонтальной силой 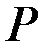. Модуль Юнга равен 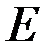, геометрические размеры: , .

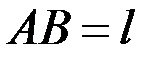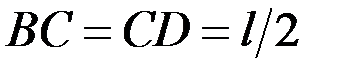Задача 12

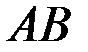Определить внутренние усилия и перемещения на участке консольного пространственного бруса 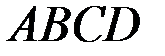круглого сечения диаметром 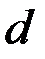, нагруженного вертикальной силой 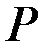. Модуль Юнга равен 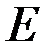, геометрические размеры: , .

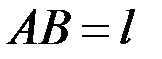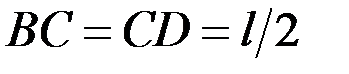Задача 13

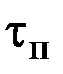Определить внутренние усилия и перемещения бруса прямоугольного сечения, нагруженного по верхней грани касательной нагрузкой , Па. Длина бруса , модуль Юнга .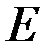

Задача 14

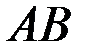Определить внутренние усилия и перемещения консольного бруса прямоу­голь­ного сечения, нагруженного растягивающей силой 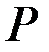с эксцентри­ситетом 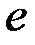. Длина бруса , модуль Юнга .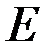

Задача 15

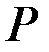Определить внутренние усилия и перемещения консольной балки прямоугольного сечения, нагруженной двумя силами , модуль Юнга равен 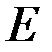. Размеры указаны на рисунке.

Задача 16

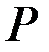Определить внутренние усилия и перемещения консольной балки прямоугольного сечения, нагруженной силой и имеющей удельный вес 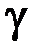. Модуль Юнга равен 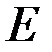, размеры указаны на рисунке.

Задача 17

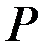Определить внутренние усилия и перемещения консольной балки прямоугольного сечения, нагруженной консольной силой . Модуль Юнга 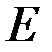, размеры указаны на рис