Формулировка силовых граничных условий

Для решения практических задач система дифференциальных уравнений технической теории стержней (разд. 2.4) должна быть дополнена силовыми и геометрическими (кинематическими) граничными условиями, отражающими условия закрепления стрежня и условия нагружения на его концах.

Возможны два варианта записи силовых граничных условий:

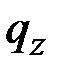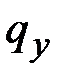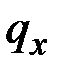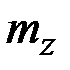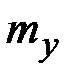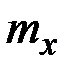1. Если силы и моменты, приложенные к концам стержня, включаются в выражения погонных силовых и моментных нагрузок , , и , , , то во всех задачах силовые граничные условия являются однородными, т. е.

, , , , , ;

, , , , , .

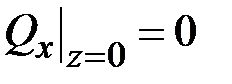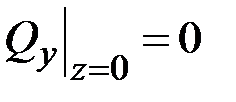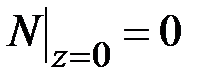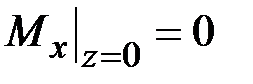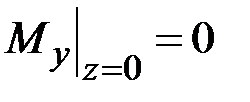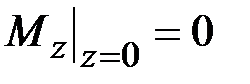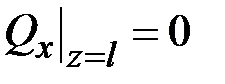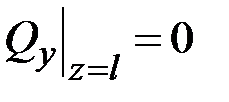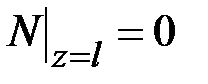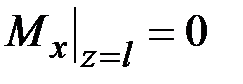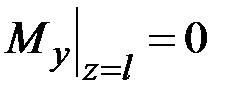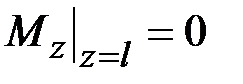2. Если силы и моменты, приложенные к концам стержня, не включаются в выражения погонных нагрузок 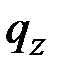, , 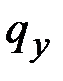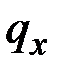и 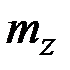, , 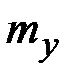, 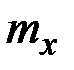то тогда в каждой задаче имеют место свои силовые граничные условия вида

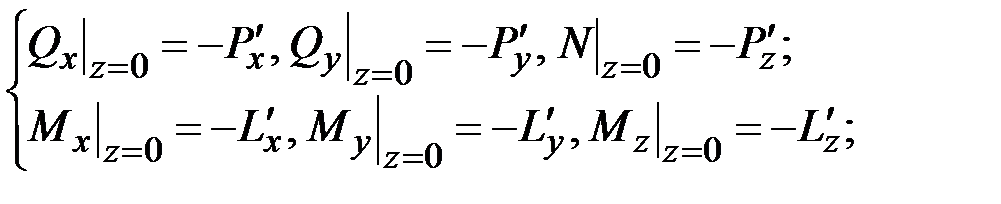(4.21)

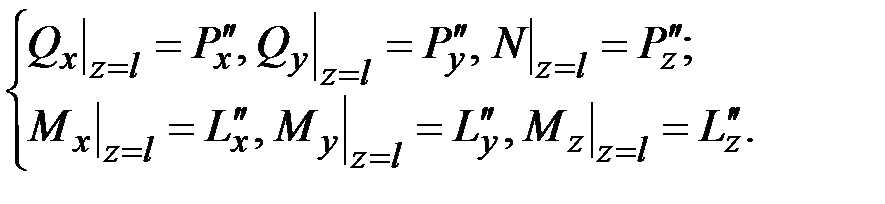(4.22)

Здесь 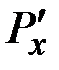, , 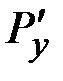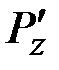– компоненты внешней силы 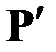, а 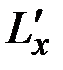, , 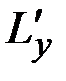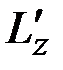– составляющие момента внешних сил 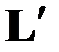, приложенных к левому концу стержня 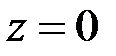. Соответственно, 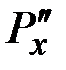, , 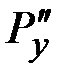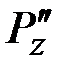– компоненты внешней силы 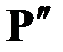, а 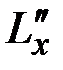, , 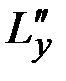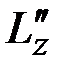– составляющие момента внешних сил 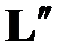, приложенных к правому концу стержня 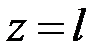. Наличие знака минус в (4.21) и его отсутствие в (4.22) является следствием ранее принятого соглашения о знаках внутренних силовых факторов для «левой» и «правой» сторон одного и того же поперечного сечения стержня (разд. 1.7) и интегральных уравнений равновесия (1.14), (1.15).

Оба варианта записи силовых граничных условий абсолютно равноправны, выбор того или иного варианта определяется соображениями простоты. Так, первый вариант записи удобен при выводе энергетических соотношений. Второй вариант записи граничных условий удобен при интегрировании системы дифференциальных уравнений (2.57)–(2.60).

5. Типовые примеры решения
задач сопротивления материалов

Проиллюстрируем применение универсального метода решения задач сопротивления материалов с использованием обобщённой функции Дирака и единичной функции Хевисайда на нескольких типовых примерах, расположенных по мере возрастания их сложности.

Расчёт балки на изгиб

Порядок записи силовых граничных условий (4.21), (4.22) поясним на примере решения статически определимой задачи изгиба стержня постоянной жёсткости (рис. 5.1).

Рис. 5.1. Изгиб стержня постоянной жёсткости

Предварительно определим реакции опор. Для этого запишем уравнение равновесия в проекции на ось и уравнение моментов относительно точки :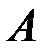

, .

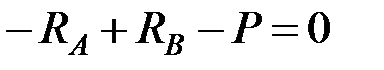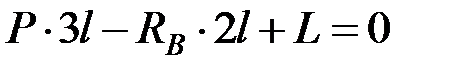Отсюда находим

, .

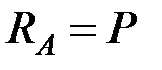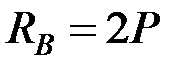Изгиб стержня описывается системой уравнений (2.59):

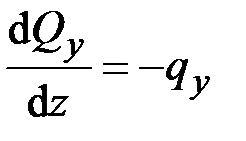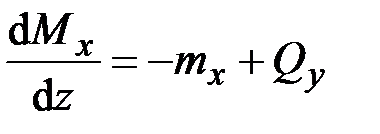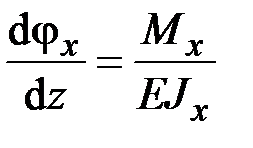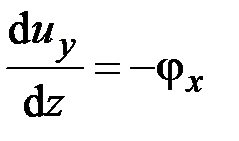, , , , (5.1)

которые следует дополнить силовыми граничными условиями

, , , ,

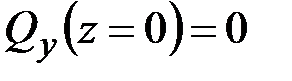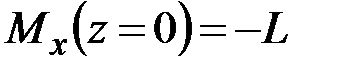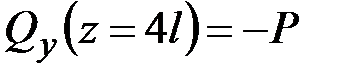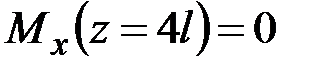и кинематическими граничными условиями

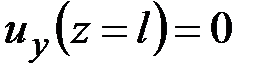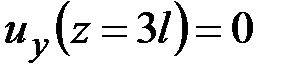, . (5.2)

Согласно рис. 5.1 внешние погонные нагрузки равны

z – l

, .

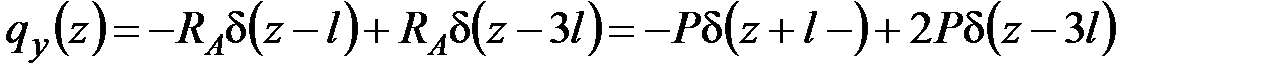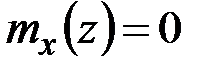Интегрируя первое уравнение (5.1) от нуля до 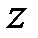, имеем

.

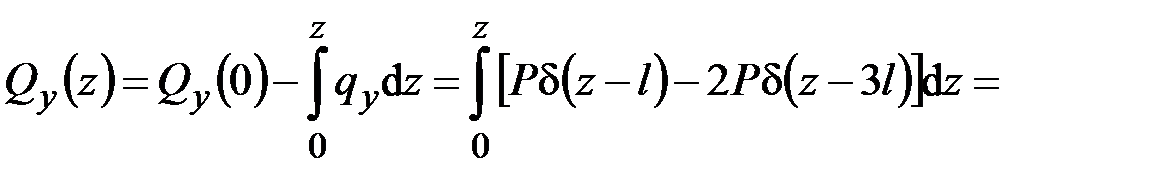
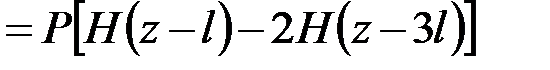Подставляя выражение для 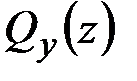во второе уравнение (5.1), находим

.

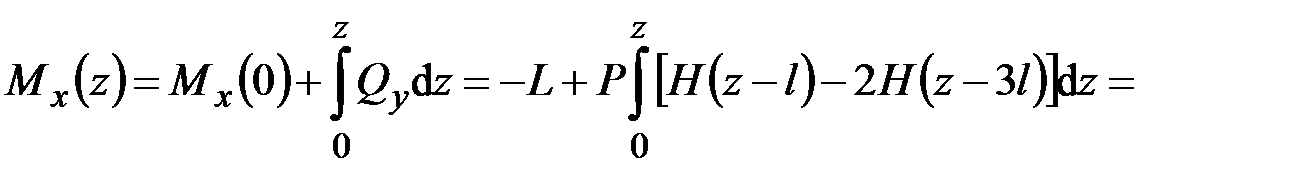
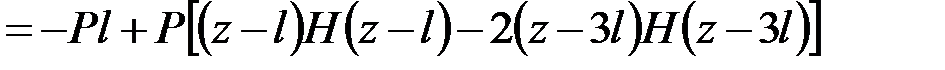Затем, подставив значение 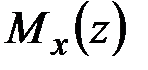в третье уравнение (5.1), получаем

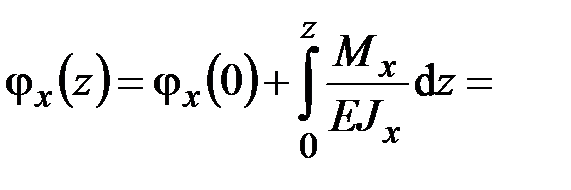
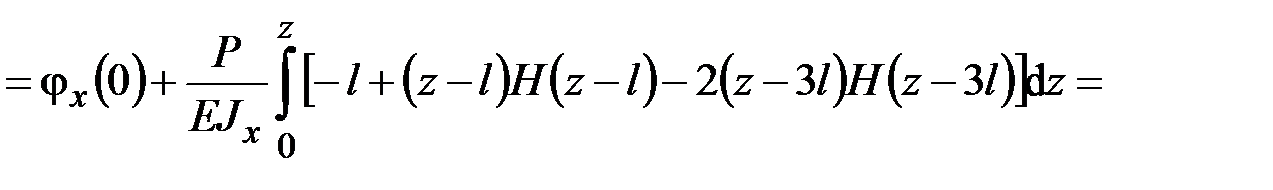
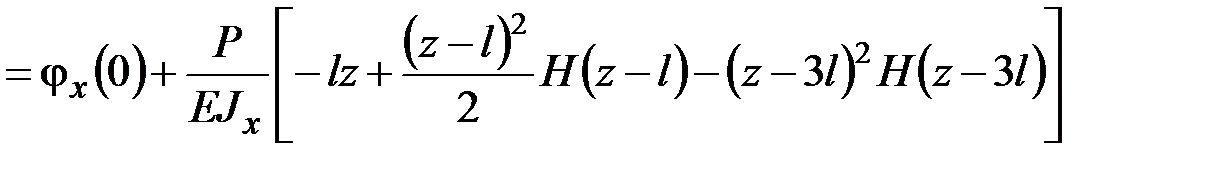. (5.3)

Наконец, подставляя значение 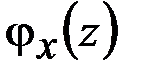в последнее уравнение (5.1), имеем

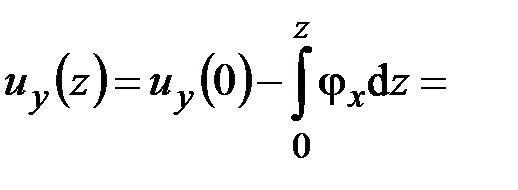
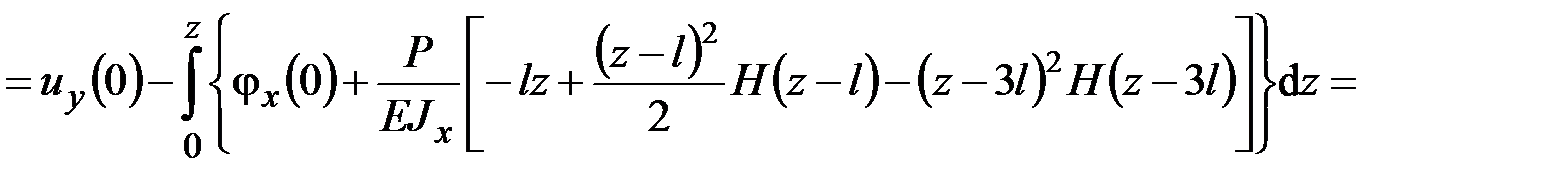
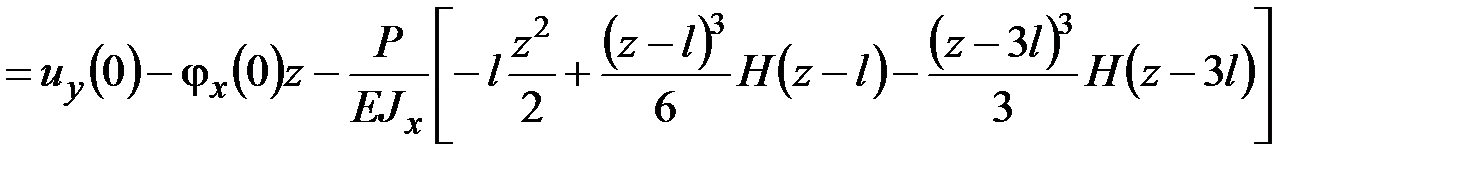. (5.4)

Чтобы отыскать постоянные интегрирования 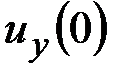, 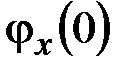– прогиб и угол поворота поперечного сечения левого конца стержня, обратимся к кинематическим граничным условиям (5.2):

,

.

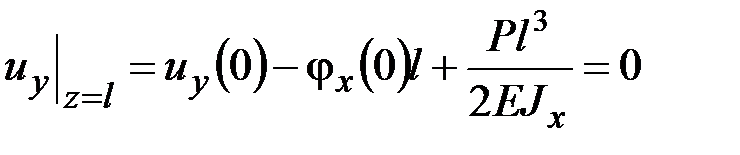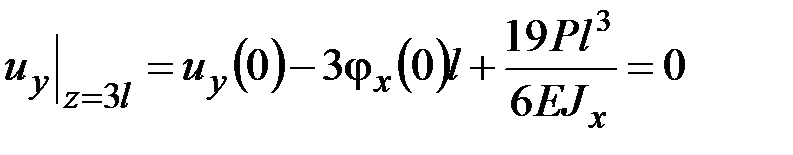Решая данную систему двух алгебраических уравнений, находим

, .

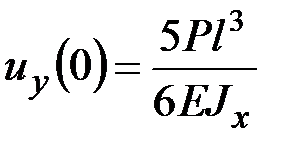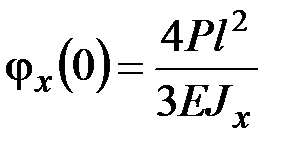В результате выражения (5.3), (5.4) для углов поворотов 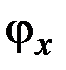и прогибов 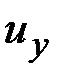полностью определённы.