Статические (динамические) уравнения

Чтобы установить дифференциальные уравнения равновесия, рассмотрим бесконечно малый элемент стержня (рис. 2.1).

Рис. 2.1. Равновесие бесконечно малого элемента стержня

До нагружения стержень имеет длину 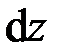, после нагружения – длину 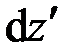(рис. 2.1, а). Величина

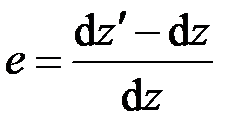
определяет относительное удлинение элемента оси стержня. Отсюда

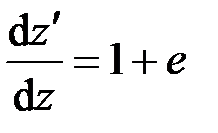. (2.1)

С другой стороны, для элемента оси стержня после деформации имеем

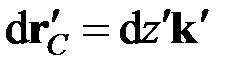, (2.2)

где 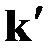– орт касательной к изогнутой оси стержня (рис. 1.12).

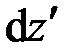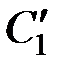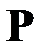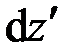В соответствии с правилом о знаках (разд. 1.6) в сечении элемента стержня с центром тяжести действует сила и момент , взятые с обратным знаком (рис. 2.1, б), поскольку для стрежня в целом данное сечение является «правым» сечением. В сечении элемента стержня с центром тяжести 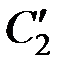, являющимся «левым» сечением для стрежня в целом, действует сила 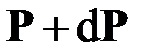и момент 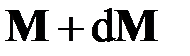(рис. 2.1, б). Здесь 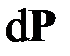, 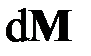– бесконечно малые приращения, вызванные действием главного вектора 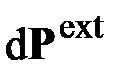и главного момента 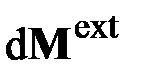внешних сил, приведённых к срединной точке оси элемента стержня (рис. 2.1, б). При равновесии сумма всех сил и сумма моментов всех сил относительно любой точки, например точки 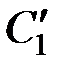, должна быть равна нулю:

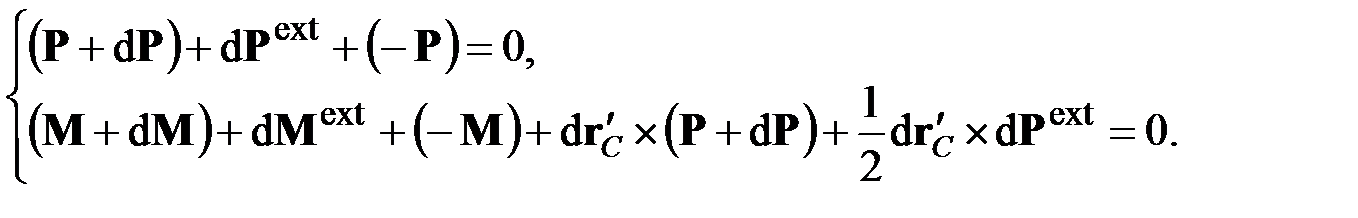(2.3)

Отбросив слагаемые второго порядка малости, разделим (2.3) на 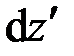и примем во внимание (2.2). В результате получим

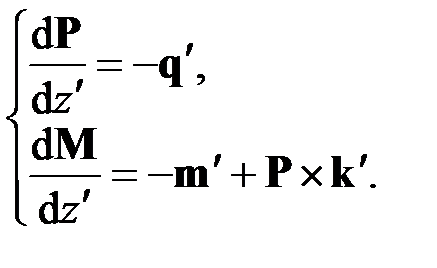(2.4)

Здесь

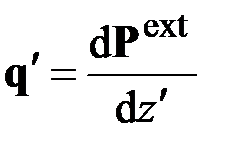(2.5)

– внешняя сила, приходящаяся на единицу длины деформированного стержня,

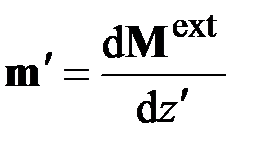(2.6)

– момент внешних сил на единицу длины деформированного стержня.

Если разделить (2.3) на и проделать аналогичные выкладки со ссылкой на (2.1), будем иметь

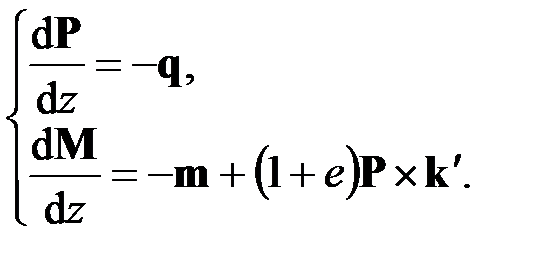(2.7)

Здесь уже

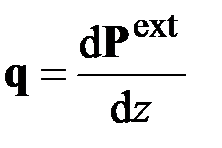(2.8)

– внешняя сила на единицу длины недеформированного стержня,

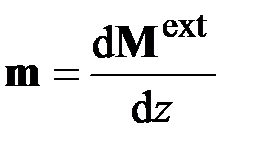(2.9)

– момент внешних сил на единицу длины недеформированного стержня. Величины (2.5), (2.6) и (2.8), (2.9) связаны между собой равенствами

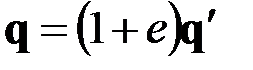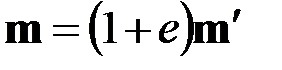, , (2.10)

ибо

, .

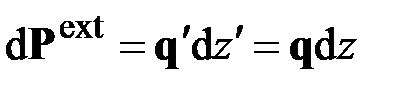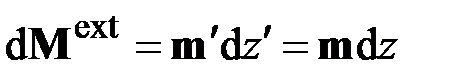В случае малых деформаций в (2.7), (2.10) можно пренебречь величиной 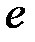по сравнению с единицей, так как при упругом деформировании 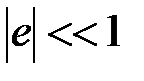. Для малых перемещений приближённо 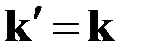. С учётом всех этих обстоятельств обе формы уравнений равновесия (2.4), (2.7) принимают одинаковый вид

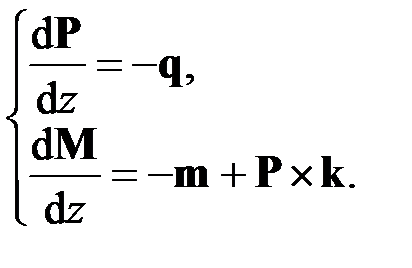(2.11)

Причём

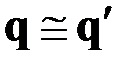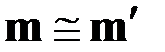, . (2.12)

В приближении (2.12) величину 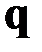называют распределённой (погонной) силовой нагрузкой, а величину 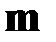– распределённой (погонной)
моментной нагрузкой без указания на то, к какому состоянию стержня (деформированному или недеформированному) отнесены данные вели­чины.

Чтобы из уравнений статики (2.11) получить уравнения динамики, достаточно воспользоваться принципом Даламбера и добавить к распределённым внешним нагрузкам 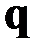, 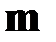распределённые инерционные нагрузки , :

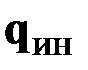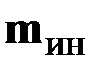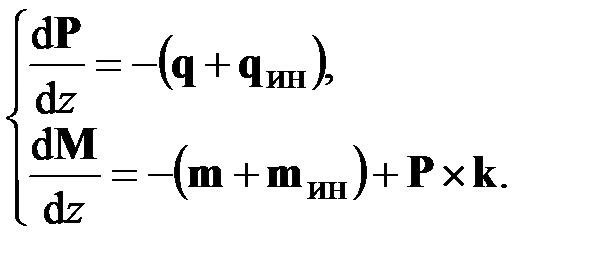(2.13)

Распределённая инерционная нагрузка 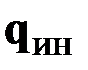– это даламберова сила инерции, приходящаяся на единицу длины стержня. Она может быть определена из цепочки равенств

,

где 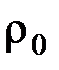– плотность материала стержня в недеформированном состоянии, 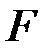– площадь поперечного сечения, 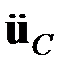– ускорение центра масс элемента стержня длиной 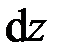(см. рис. 1.12, рис. 2.1). Значит,

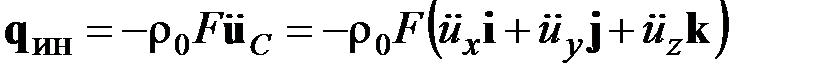, (2.14)

где 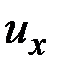, , 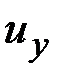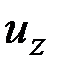– компоненты вектора перемещения 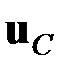центра тяжести поперечного сечения стержня (рис. 1.12).

Распределённая инерционная нагрузка 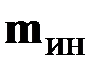– это момент сил инерции, приходящийся на единицу длины стержня:

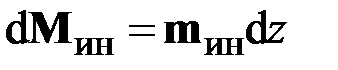. (2.15)

По динамическим уравнениям Эйлера, известным из курса теоретической механики, у абсолютно твёрдого тонкого диска с поперечным сечением 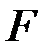и длиной тела момент сил инерции 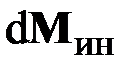в проекциях на его главные центральные оси 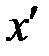, , 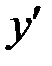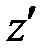определяется выражениями

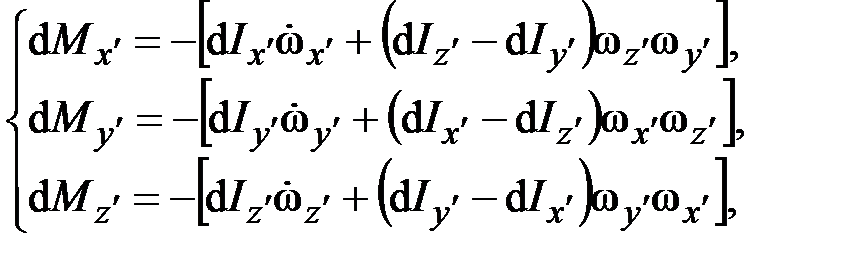
где 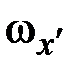, , 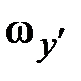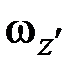– компоненты вектора угловой скорости. Главные моменты инерции тонкого диска 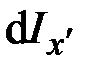, , 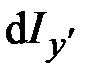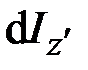связаны с осевыми моментами инерции его поперечного 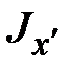сечения , и полярным моментом инерции сечения 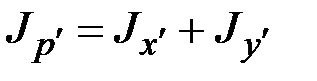следующими равенствами:

,

,

.

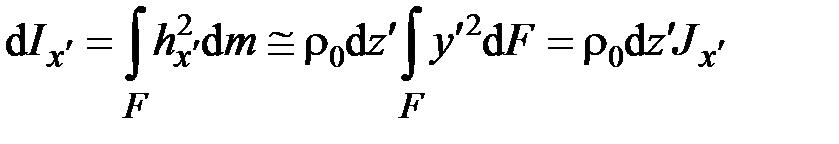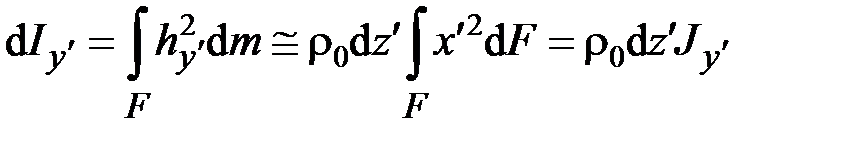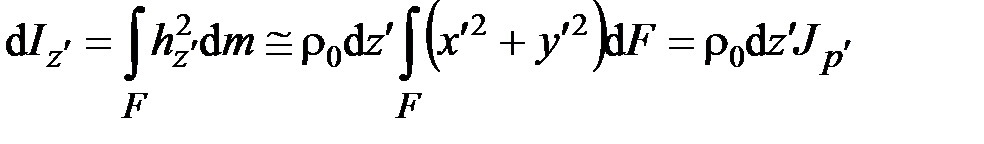Применим данные соотношения к элементу стержня бесконечно малой длины (рис. 2.1) и учтём, что (рис. 1.12)

,

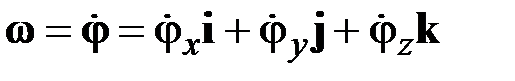где 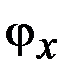, , 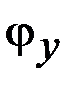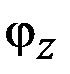– компоненты вектора поворота 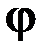поперечного сечения вокруг его центра тяжести (рис. 1.12). Благодаря условию малости перемещений приближенно будем иметь

.

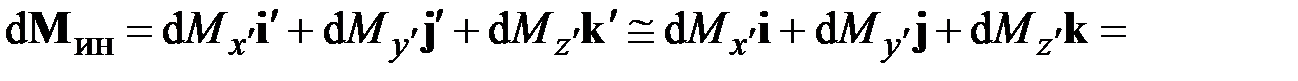
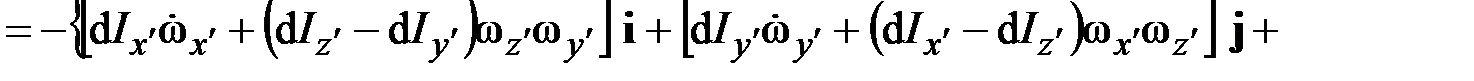
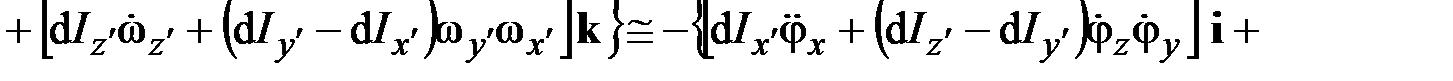
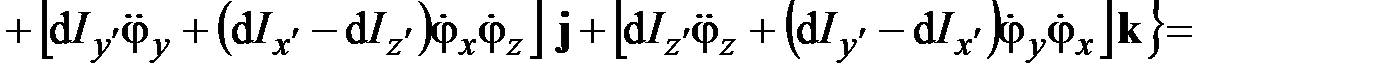
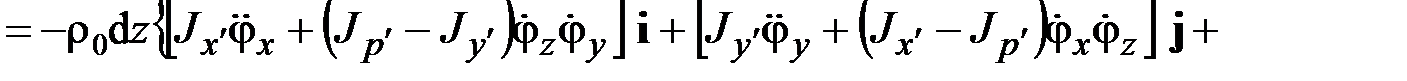
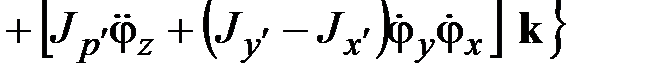Сравнив данное выражение с (2.15), получим

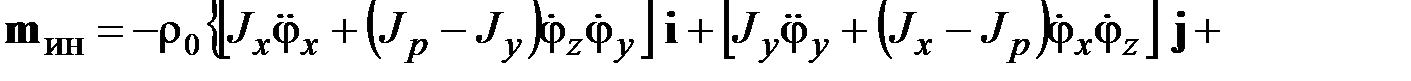
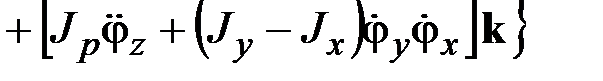. (2.16)

Если малыми являются не только компоненты вектора поворота 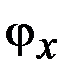, , 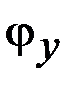, 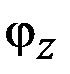но и компоненты вектора угловой скорости 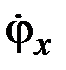, , 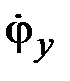, 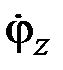то тогда выражение (2.16) упростится и примет вид

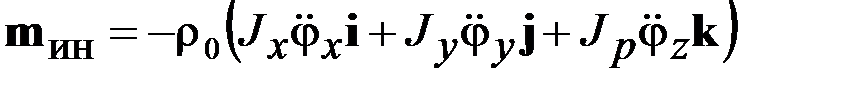. (2.17)

Запишем уравнения равновесия (2.11) в проекциях на оси координат 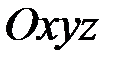(рис. 2.1). С этой целью воспользуемся разложениями

, ,

, ,

.

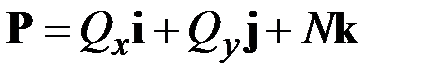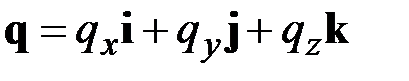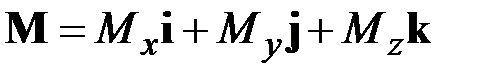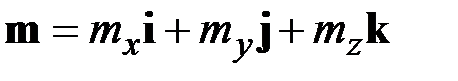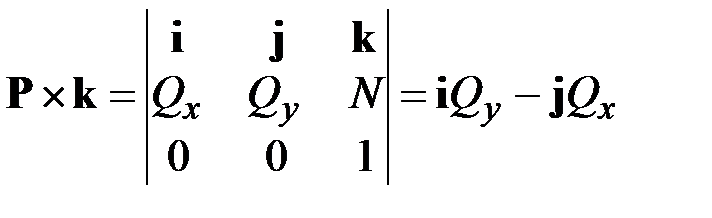В результате получим шесть уравнений относительно шести неизвестных:

, , ,

, , .

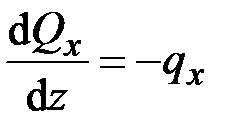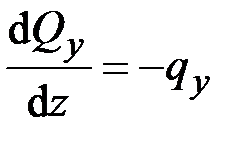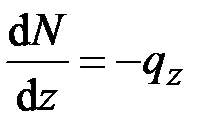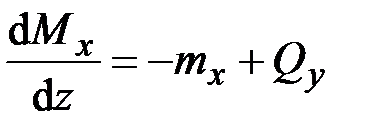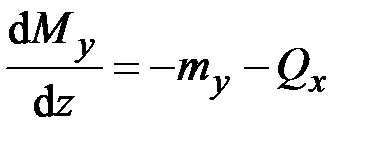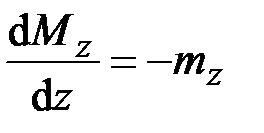Данные уравнения целесообразно разбить на четыре группы:

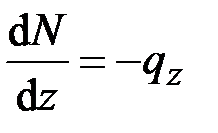, (2.18)

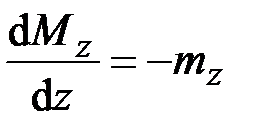, (2.19)

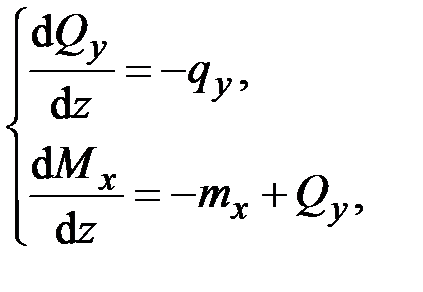(2.20)

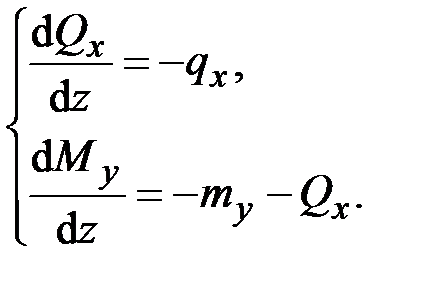(2.21)

Уравнение (2.18) позволяет решать задачи на растяжение стержня и находить (с точностью до одной постоянной интегрирования) распределение продольной силы 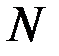по известной погонной осевой нагрузке 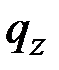. Уравнение (2.19) позволяет решать задачи на кручение стержня и находить распределение (с точностью до одной постоянной интегрирования) крутящего момента 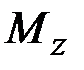по известной погонной моментной крутящей нагрузке 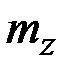. Система уравнений (2.20) описывает изгиб стержня в главной плоскости 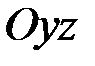(рис. 2.1) и позволяет находить (с точностью до двух постоянных интегрирования) распределение поперечной силы 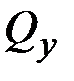и изгибающего момента 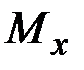по известным погонным нагрузкам 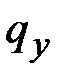, 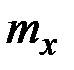– поперечной силовой и моментной изгибающей нагрузками. Наконец, система уравнений (2.21) описывает изгиб стержня в главной плоскости 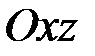(рис. 2.1) и позволяет находить (с точностью до двух постоянных интегрирования) распределение поперечной силы 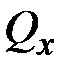и изгибающего момента 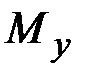по известным погонным нагрузкам 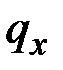, 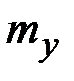– поперечной силовой и моментной изгибающей нагрузками.

В случае статически определимой задачи значения всех постоянных интегрирования определяются из соответствующих силовых граничных условий, отражающих условия нагружения концов стержня.

В динамических задачах используются уравнения движения

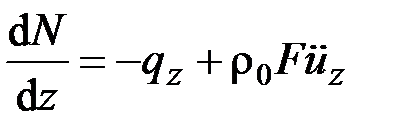, (2.22)

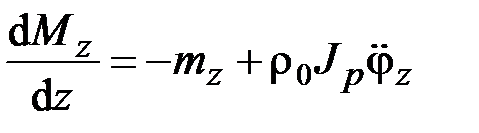, (2.23)

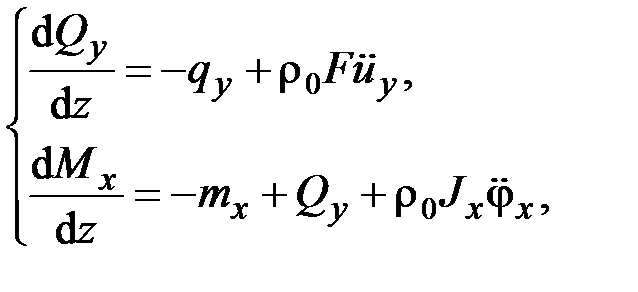(2.24)

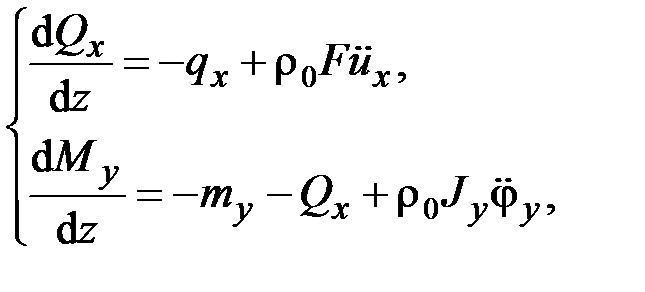(2.25)

которые вытекают из (2.13), (2.14), (2.17). В данном случае одних динамических уравнений (2.22)–(2.25) недостаточно, так как число неизвестных превышает число уравнений. Для решения задачи необходимы дополнительные уравнения.

Геометрические уравнения

Обратимся к рис. 1.12 и формулам (1.22), (2.1), согласно которым

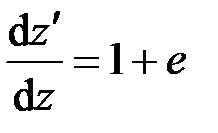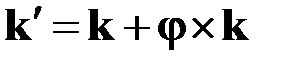, , (2.26)

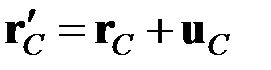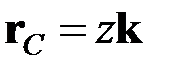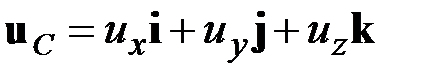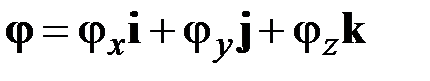, , , . (2.27)

Отсюда имеем

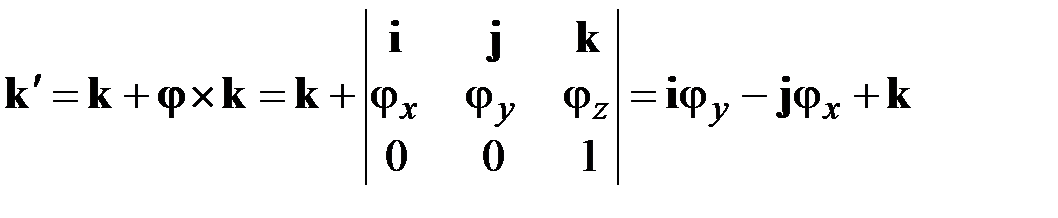. (2.28)

С другой стороны, орт касательной изогнутой оси стержня равен

.

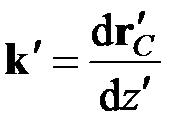Поэтому с учётом (2.26), (2.27)

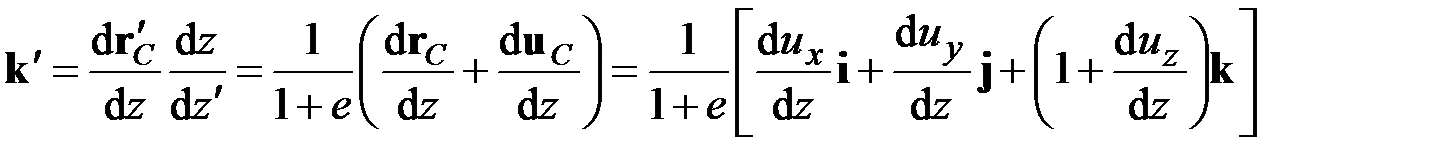. (2.29)

Приравняв (2.28) и (2.29), находим

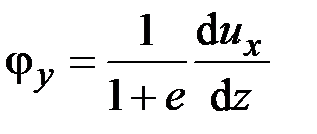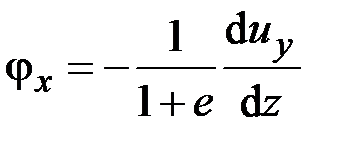, , (2.30)

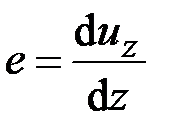. (2.31)

В приближении малых деформаций, когда относительное удлинение элементов оси стержня имеет пренебрежимо малую величину по сравнению с единицей (т. е. 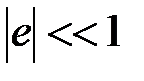), формулы (2.30) упрощаются:

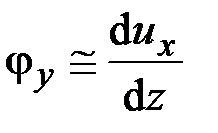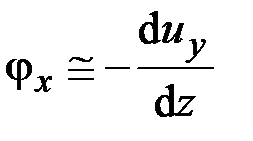, . (2.32)

Однако формула (2.31) и в этом случае сохранят свою значимость.

Таким образом, из шести компонент вектора перемещения 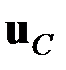и вектора поворота 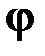независимыми являются только четыре компоненты. В качестве таковых удобно взять компоненты

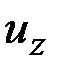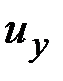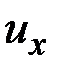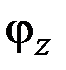, , , , (2.33)

каждая из которых отвечает растяжению, изгибу в главной плоскости 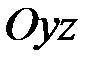, изгибу в главной плоскости 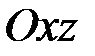и кручению стержня соответственно. Остальные две компоненты – углы поворота 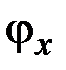, , 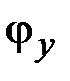включая относительное удлинение элементов оси 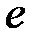, определяются из выражений (2.31) и (2.32), которые можно рассматривать как кинематические ограничения, накладываемые гипотезой плоских сечений на перемещения стержня.

Растяжение. Рассмотрим сначала деформацию чистого растяжения, когда из величин (2.33) только 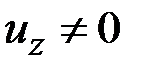. Записав размерную цепочку
(рис. 2.2, а)

,

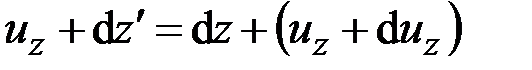получим

.

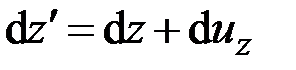Значит, при чистом растяжении относительное удлинение материальных отрезков, параллельных оси стержня, одинаково по величине:

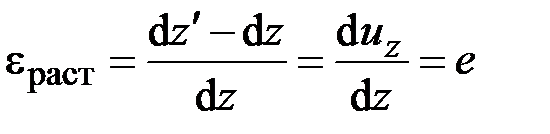. (2.34)

Поэтому при упругом изотермическом растяжении в соответствии с законом Гука (1.19) в поперечных сечениях стержня возникают равномерно распределённые нормальные напряжения (рис. 2.2, б)

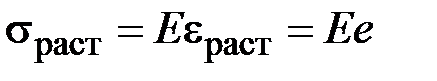. (2.35)

Рис. 2.2. Чистое растяжение стержня

Изгиб в плоскости . Рассмотрим далее деформацию чистого изгиба в главной плоскости 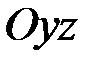, когда из величин (2.33) только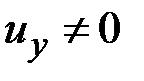
(рис. 2.3). Так как 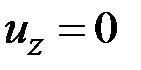, из формул (2.31), (2.1) следует, что

= 0,

; .

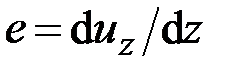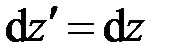Рис. 2.3. Чистый изгиб в главной плоскости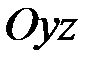

Значит, элемент оси 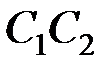(рис. 2.3, а) при изгибе сохраняет свою длину,
а другие элементарные отрезки, параллельные оси, либо растягиваются, либо удлиняются. Иными словами, глядя на рис. 2.3, а и полагая 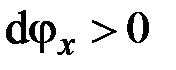, имеем

, , ,

, .

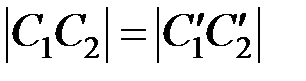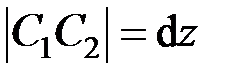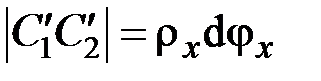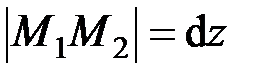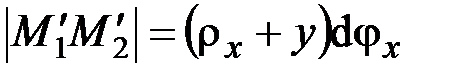Следовательно,

, .

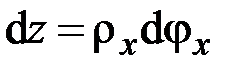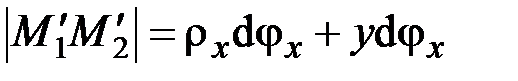Отсюда получается выражение

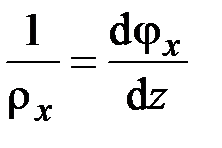, (2.36)

определяющее алгебраическое значение радиуса кривизны изогнутой оси стержня, а также выражение для относительного удлинения материального элемента 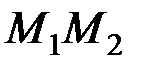, параллельного оси стержня (рис. 2.3):

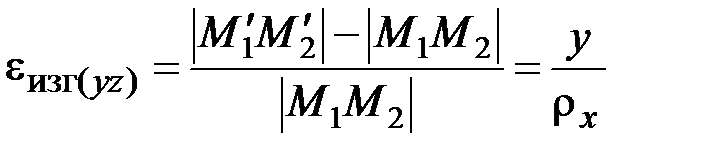. (2.37)

Из (2.36) следует, что радиус кривизны изогнутой оси стержня 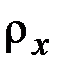имеет положительное (отрицательное) алгебраическое значение, если угол поворота поперечного сечения является возрастающей (убывающей) функцией 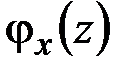. Если 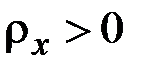, то согласно (2.37) при 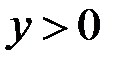имеет место растяжение, а при 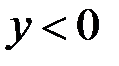– сжатие соответствующего материального элемента.

При изотермическом изгибе в поперечных сечениях стержня возникают нормальные напряжения, распределённые в соответствии с законом Гука (1.19) и формулой (2.37) по линейному закону (рис. 2.3, б):

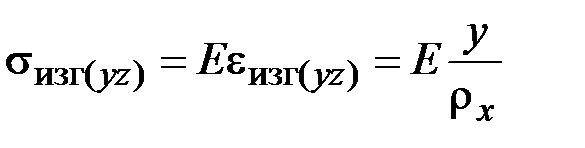. (2.38)

Изгиб в плоскости 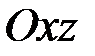. Аналогичный результат получается при рассмотрении деформации чистого изгиба в главной плоскости 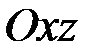, когда из величин (2.33) только 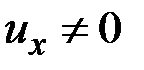(рис. 2.4). Поскольку 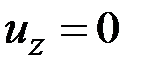, то, как и ранее, 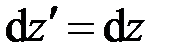. Поэтому при 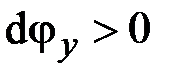из рис. 2.4, а имеем

, , ,

, .

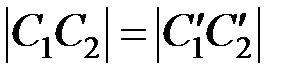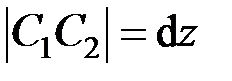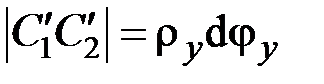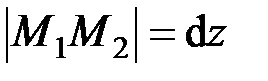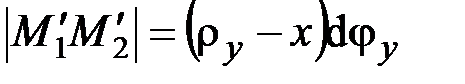Следовательно,

, .

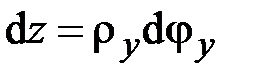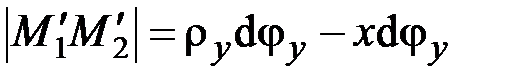Отсюда вытекает выражение для алгебраического значения радиуса кривизны изогнутой оси стержня

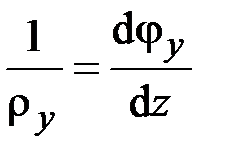, (2.39)

а также выражение для относительного удлинения материального элемента 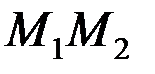, параллельного оси стержня (рис. 2.4, а):

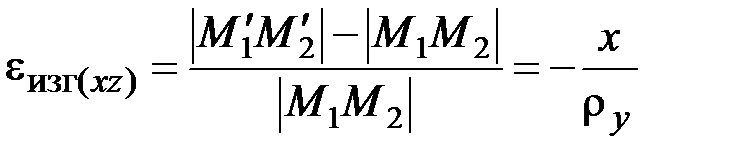. (2.40)

Рис. 2.4. Чистый изгиб в главной плоскости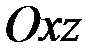

Из (2.39) следует, что радиус кривизны изогнутой оси стержня 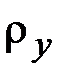принимает положительное (отрицательное) алгебраическое значение, если угол поворота поперечного сечения является возрастающей (убывающей) функцией 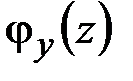. Если 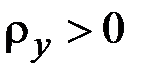, то в согласии с (2.40) при 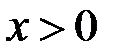имеет место сжатие, а при 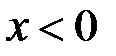– растяжение соответствующего материального
элемента.

При изотермическом изгибе в поперечных сечениях стержня возникают нормальные напряжения, распределённые в соответствии с законом Гука (1.19) и формулой (2.40) по линейному закону (рис. 2.4, б):

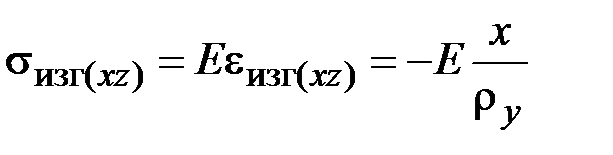. (2.41)

Кручение. Рассмотрим чистое кручение, когда из всех величин (2.33) лишь 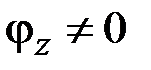. В этом случае торцы элемента стержня длиной 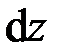поворачиваются на относительный угол 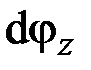(рис. 2.5, а). За счёт этого на цилиндрической поверхности радиуса 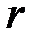наблюдается сдвиговая деформация мысленно нанесённой сетки. Угол сдвига 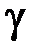определяется равенством (рис. 2.5, а)

.

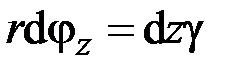Следовательно,

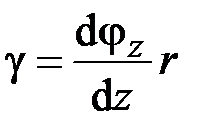. (2.42)

В соответствии с законом Гука (1.21) в поперечных сечениях стержня возникают касательные напряжения (рис. 2.5, б), которые с учётом (2.42) распределены по линейному закону (рис. 2.5, в):

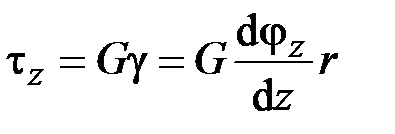. (2.43)

Рис. 2.5. Кручение стержня

По закону парности касательных напряжений (рис. 2.5, б) такое же распределение касательных напряжений имеет место и в диаметральных плоскостях продольных сечений стержня (рис. 2.6).

Рис. 2.6. Распределение касательных напряжений при кручении

Нетрудно заметить (рис. 2.5, а), что отрезки длиной 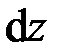, параллельные оси стержня до деформации, после деформации имеют длину

.

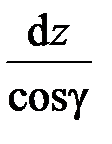Поэтому их относительное удлинение равно

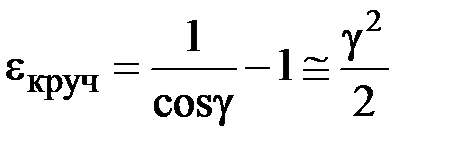. (2.44)

При упругом деформировании угол сдвига (2.42) крайне мал (для стали порядок максимального значения 10^–3 рад). Поэтому величина (2.44) имеет второй порядок малости и ей можно пренебречь по сравнению с относительными удлинениями при растяжении и изгибе.

В общем случае малых перемещений стержня относительное удлинение элементарных отрезков, параллельных оси стержня до деформации, складывается из относительных удлинений при растяжении и изгибе:

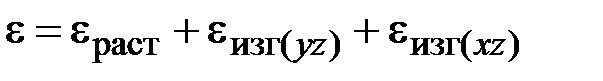. (2.45)

С учётом (2.34), (2.37), (2.40) формула (2.45) принимает вид

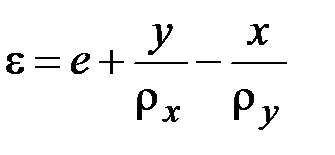. (2.46)

Если же принять во внимание (2.36), (2.39), будем иметь

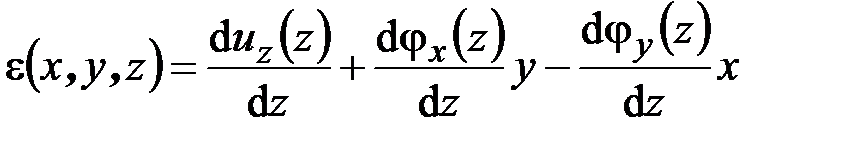. (2.47)

В записи формулы (2.47) отражена структура зависимости относительного удлинения от координат точек стержня, являющихся началом бесконечно малых элементов стержня, нормальных к поперечным сечениям, как до деформации, так и после деформации (рис. 2.2, рис. 2.3, а, рис. 2.4, а).

Если привлечь зависимости (2.32), то тогда (2.47) перепишется так:

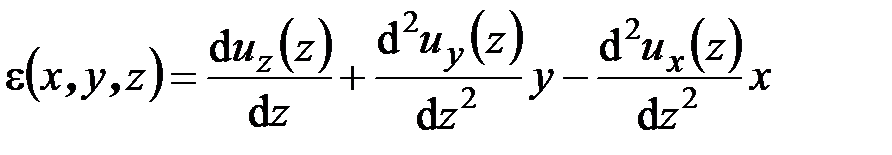. (2.48)

Как видим, относительная деформация в данной точке стержня полностью определяется через перемещения точек оси стержня.

Физические уравнения

Деформации относительного удлинения (2.47) и сдвига (2.42) связаны законом Гука (1.19), (1.21) с нормальными напряжениями 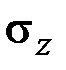и касательными напряжения 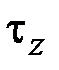, действующими в поперечном сечении стержня (рис. 2.7):

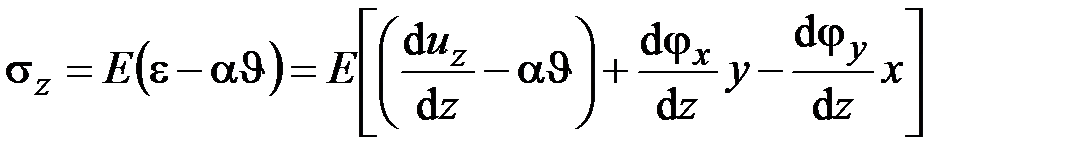, (2.49)

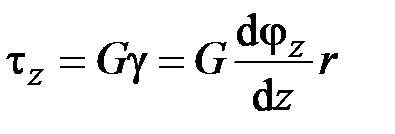. (2.50)

Рис. 2.7. Нормальные и касательные напряжения в сечении

Располагая выражениями (2.49) и (2.50), можно вычислить внутренние силовые факторы (1.9):

,

,

,

.

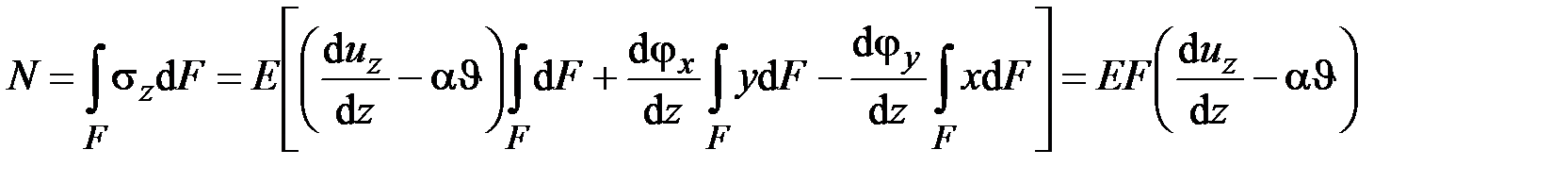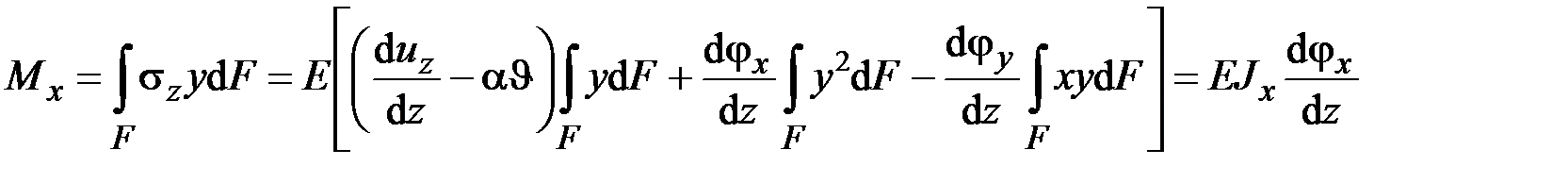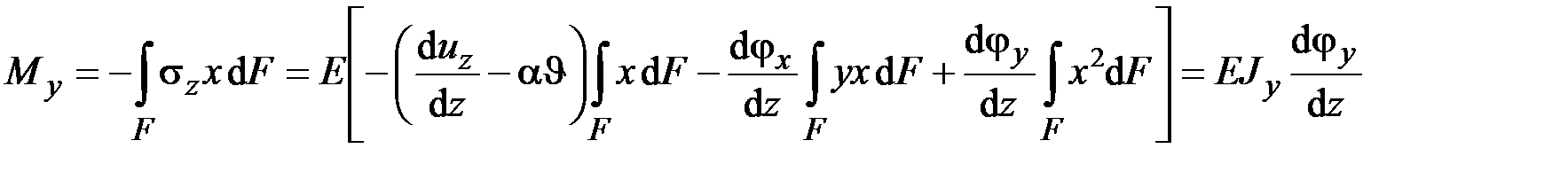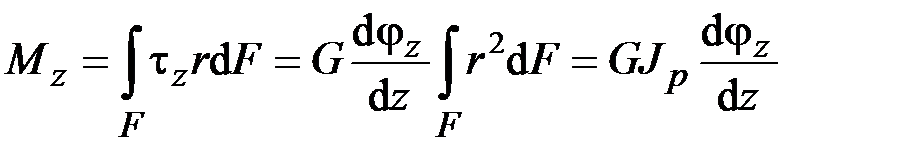Здесь принято во внимание, что оси , являются главными центральными осями поперечного сечения стержня (разд. 1.1).

Таким образом, внутренние силовые факторы связаны с геометрическими характеристиками деформации и тепловым расширением стержня следующими определяющими соотношениями:

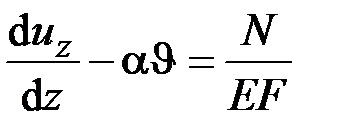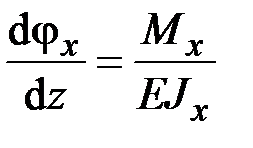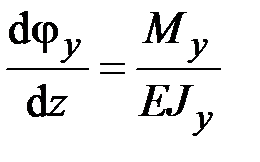, , , (2.51)

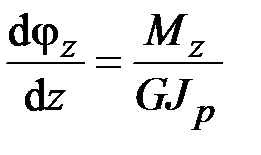. (2.52)

Подставив (2.51), (2.52) в (2.49), (2.50), можно выразить распределение нормальных и касательных напряжений в сечении через внутренние силовые факторы:

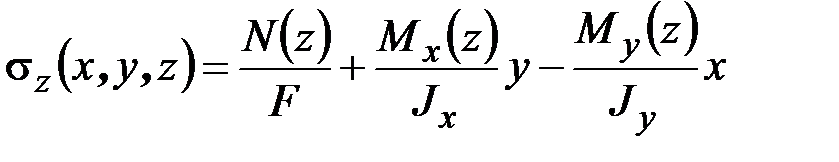, (2.53)

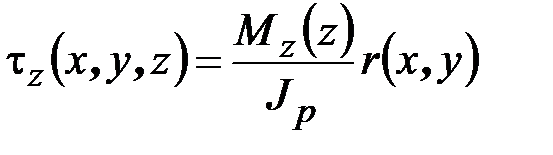. (2.54)

Выражение (2.53) называется трёхчленной формулой Навье. Данная формула вместе с формулами (2.51) составляет основу технической теории прямых стержней произвольного поперечного сечения. По формуле (2.53) нормальные напряжения линейно зависят от координат 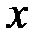, 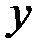точек поперечного сечения стержня.

Рис. 2.8. Типовые поперечные сечения

Формулы (2.52), (2.54), в которые входит полярный момент инерции 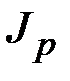и полярный радиус 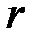, справедливы только для стержней круглого (рис. 2.8, а) и кольцевого (рис. 2.8, б) поперечного сечения. Для остальных видов сечений, например прямоугольного (рис. 2.8, в), коробчатого (рис. 2.8, г), двутаврового (рис. 2.8, д), таврового (рис. 2.8, е), уголкового (рис. 2.8, ж) и т. п., формула (2.52) заменяется формулой

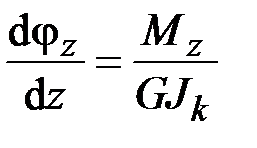, (2.55)

а скалярная формула (2.54) – векторной формулой

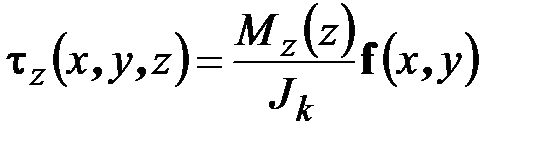. (2.56)

Здесь 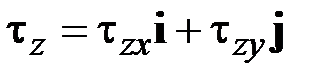– вектор касательных напряжений, 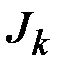– геометрический параметр, называемый моментом инерции сечения при кручении, 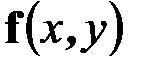– некоторая векторная функция. Указанные величины не могут быть определены элементарными методами сопротивления материалов. Данный вопрос решается методами теории упругости. И только для круглого и кольцевого сечений

, .

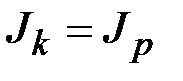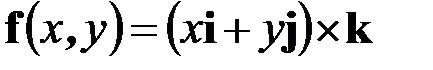2.4. Полная система дифференциальных уравнений
технической теории стержней

Соберём вместе результаты (2.18)–(2.21), (2.32), (2.51), (2.55), сгруппировав их по типам напряжённо-деформированного состояния стержня.

Растяжение (сжатие) прямого стержня:

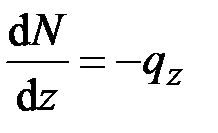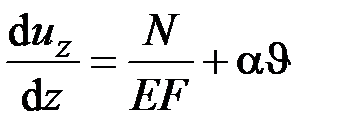, . (2.57)

Кручение прямого стержня:

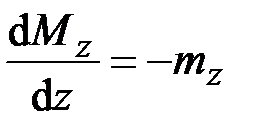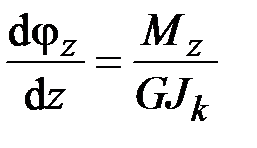, . (2.58)

Изгиб прямого стержня в главной плоскости :

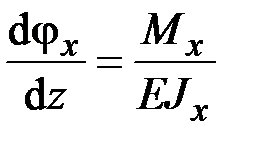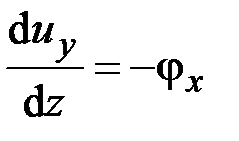, , , . (2.59)

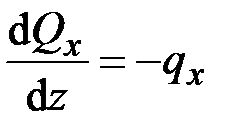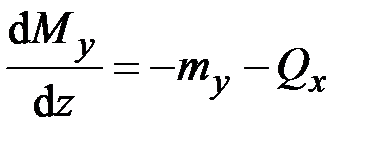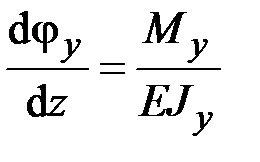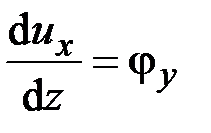, , , . (2.60)

При известных внешних силовых нагрузках 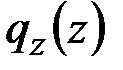, , 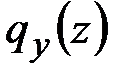, 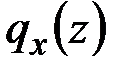внешних моментных нагрузках 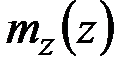, , 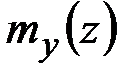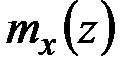и температурном воздействии на стержень 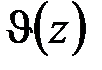система 12 обыкновенных дифференциальных уравнений (2.57)–(2.60) позволяет находить 12 неизвестных величин
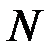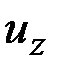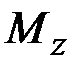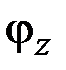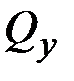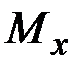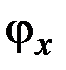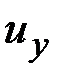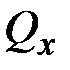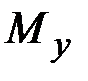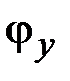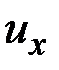( , ; , ; , , , ; , , , ) с точностью до 12 постоянных интегрирования, определяемых из граничных условий.

После этого по соответствующим формулам можно найти распределение нормальных и касательных напряжений в поперечных сечениях стержня.