Линейные однородные системы дифференциальных уравнений (ЛОС ДУ).
ЛОС ДУ для функции y(x), z(x) называется система уравнений вида
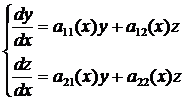 (3.1)
(3.1)
где 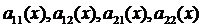 - непрерывные на (a,b) функции.
- непрерывные на (a,b) функции.
Свойства решений ЛОС ДУ (3.1).
1. Сумма двух решений системы (3.1) – тоже решение этой системы.
Доказательство:
Пусть 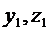 и
и 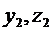 – два каких-либо решения системы (3.1). Тогда
– два каких-либо решения системы (3.1). Тогда
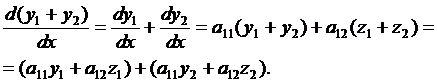
Но 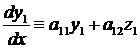 и
и 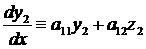 .
.
Аналогично рассматривается и второе уравнение системы (3.1).
2. Если y(x), z(x) – решение ЛОС ДУ и c – произвольная константа, то cy(x), cz(x) – тоже решение (3.1). Доказательство свойства аналогично доказательству свойства 1.
Следствие.
Если  и
и 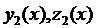 - решения системы (3.1), то выражение вида
- решения системы (3.1), то выражение вида
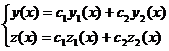
где 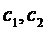 - произвольные постоянные, тоже решение (3.1).
- произвольные постоянные, тоже решение (3.1).
Определение 1. Система функций 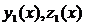 и
и 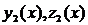 называется линейно независимой на некотором интервале (a,b), если из системы равенств
называется линейно независимой на некотором интервале (a,b), если из системы равенств
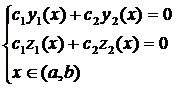 (3.2)
(3.2)
Следует, что 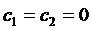
В противном случае система функций 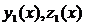 и
и 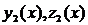 - линейно зависима на (a,b).
- линейно зависима на (a,b).
Определение 2. Определитель, составленный для системы функций 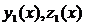 и
и 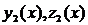 называется определителем Вронского и обозначается W(x). Итак
называется определителем Вронского и обозначается W(x). Итак
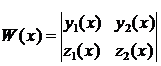 .
.
Теорема 1. Определитель Вронского для линейно независимой на интервале (a,b) системы решений 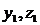 и
и 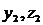 ЛОС ДУ не равен нулю ни в одной точке (a,b).
ЛОС ДУ не равен нулю ни в одной точке (a,b).
Доказательство.
Докажем теорему методом от противного. Предположим, что существует точка 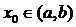 , в которой
, в которой
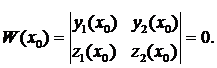
Составим линейную однородную систему уравнений с неизвестными 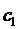 и
и 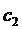 :
: 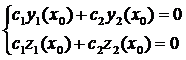 (3.3)
(3.3)
Так как определитель системы (3.3) равен нулю, то система имеет бесконечное множество ненулевых решений. Пусть 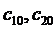 - одно из них. С помощью этих констант и двух линейно независимых на (a,b) решений системы (3.1)
- одно из них. С помощью этих констант и двух линейно независимых на (a,b) решений системы (3.1) 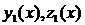 и
и 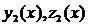 составим две функции
составим две функции
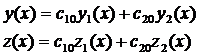 (3.4)
(3.4)
Согласно следствию из свойств решений ЛОС ДУ функции (3.4) являются решениями системы (3.1), которые в силу (3.3) в точке 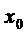 обращаются в нуль. Следовательно, y(x), z(x) – решение следующей задачи Коши:
обращаются в нуль. Следовательно, y(x), z(x) – решение следующей задачи Коши:
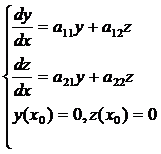
Но таким решением может быть только нулевое решение: y(x)=0, z(x)=0 при 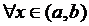 , т.е.
, т.е.
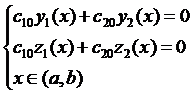
Причем 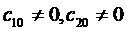 . Это означает, что система функций
. Это означает, что система функций 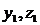 и
и 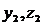 линейно зависима на (a,b), что противоречит условию теоремы. Значит наше предположение о существовании на (a,b) точки
линейно зависима на (a,b), что противоречит условию теоремы. Значит наше предположение о существовании на (a,b) точки 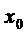 , в которой
, в которой 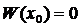 , неверно, что и доказывает теорему.
, неверно, что и доказывает теорему.
Определение 2. Линейно независимые на (a,b) решения ЛОС ДУ 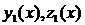 и
и 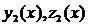 называются фундаментальной системой решений системы (3.1).
называются фундаментальной системой решений системы (3.1).
Теорема 2. Если семейство функций 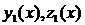 и
и 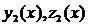 образует фундаментальную систему решений ЛОС ДУ (3.1), то их линейная комбинация
образует фундаментальную систему решений ЛОС ДУ (3.1), то их линейная комбинация

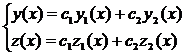 , (3.5)
, (3.5)
где 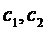 - произвольные постоянные, дает общее решение системы (3.1)
- произвольные постоянные, дает общее решение системы (3.1)
Доказательство.
1. Выражение (3.5), согласно следствию из свойств решений ЛОС ДУ, является решением системы уравнений (3.1).
2. Докажем, что (3.5) – общее решение (3.1), т.е. докажем, что каковы бы ни были начальные условия задачи Коши 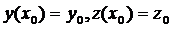 , всегда найдутся значения постоянных
, всегда найдутся значения постоянных 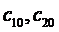 такие, что выделенное из общего частное решение ЛОС ДУ:
такие, что выделенное из общего частное решение ЛОС ДУ:
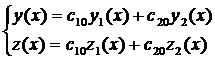
будет удовлетворять этим условиям. Для этого подставим в (3.5) начальные условия:
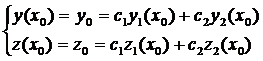 (3.6)
(3.6)
Определителем этой алгебраической системы линейных уравнений является определитель Вронского 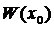 :
:
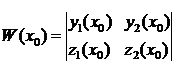 ,
,
который, согласно теореме 1, не равен нулю. Следовательно, система уравнений (3.6) имеет решение 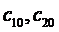 и притом единственное.
и притом единственное.
