Понятие о математическом анализе систем

Математический анализ, как известно, есть большая отрасль в математике, связанная в основном с такими формализованными понятиями, как функция, производная и интеграл. К настоящему времени эта отрасль математики обнимает большое число областей: дифференциальные уравнения, интегральные уравнения, функции комплексного переменного, дифференциальную геометрию, вариационное исчисление и др. Математический анализ систем понимается в более широком плане – как применение математических методов, в том числе математической логики, теории вероятности, математического моделирования, теории принятия решений и др. В области оптимального проектирования машин эти методы применяются давно и эффективно. Применение методов математического анализа в менеджменте качества только начинается. В данной лекции сформулированы основные методические положения по этому анализу.

Под математическим анализом систем будем понимать формализованное описание систем и проведение математическими методами исследований (в том числе с применением ЭВМ) свойств и взаимосвязей в системе с целью принятия оптимальных решений.

Формирование и развитие математического анализа систем в настоящее время идет, в основном, по трем направлениям:

1. Логический анализ систем;

2. Математическое моделирование систем;

3. Оптимизация решений, принимаемых при проектировании и эксплуатации систем.

Эти три направления между собой тесно переплетаются. Рассмотрим кратко каждое из этих направлений.

Логический анализ систем

Логический анализ систем – это проведение исследований принципов построения систем методами математической логики. В основе такого анализа лежит понятие «формальная система».

2.1. Формальная система

Под формальной (дедуктивной) системой будем понимать совокупность четырех основных множеств (Т, Р, А, В) и двух дополнительных (Г, Д):

Ф = {<Т, Р, А, В> и <Г, Д>} (11.1)

а также четырех процедур П(Т), П(Р), П(А), П(В)

В этой формуле обозначены:

Т – множество базовых элементов, состоящее из элементов х, которые не могут быть расщеплены на более мелкие элементы. Например, буквы алфавита, слова из некоторого словаря, процессы, функции и т.п. Из базовых элементов будут строиться остальные элементы формальной системы. При этом декларируется, что существует процедура П(Т), которая за конечное число шагов должна дать положительный или отрицательный ответ на вопрос: «Является ли х элементом Т?».

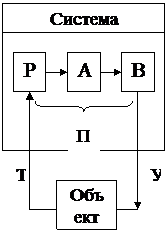Р – множество синтаксических правил, с помощью которых из элементов множества Т образуются синтаксически правильные совокупности, называемые «правильно построенные формулы» (ППФ). Например, из слов строятся синтаксически правильные фразы, из процессов формируются система менеджмента качества, из операций складывается процесс, из переходов складывается технологическая операция. При этом декларируется существование процедуры П(Р), с помощью которой за конечное число шагов можно получить ответ на вопрос: «Является ли совокупность х синтаксически правильно построенной формулой?».

А – множество аксиом, представляет собой подмножество ППФ произвольно выделенное из множества производных элементов формальной системы. Слово «аксиома» здесь не следует связывать с понятием истинности или ложности ППФ. При этом должна существовать процедура П(А), с помощью которой для любой ППФ можно получить ответ на вопрос о принадлежности ее к множеству А.

В – множество правил вывода, которые служат для того, чтобы с их помощью из множества аксиом можно было получить другие ППФ. Если имеется процедура П(В), с помощью которой можно определить для любой ППФ, является ли она выводимой, то соответствующая формальная система называется разрешимой. Правила вывода имеют общую форму записи

К => Q, (11.2) где

К – соответствует некоторой совокупности ППФ, которые либо принадлежат А, либо уже были получены из А с помощью правил вывода;

Q – совокупность ППФ, которые выводятся на данном шаге процесса вывода.

<Г,Д> – процедура интерпретации формальной системы, которая определяется двумя множествами;

Г{γ_i} – множество значений при интерпретации;

Д{γ_i} – множество правил интерпретации, где γ_i – значения (смысл), присваиваемые элементам множеств Т, Р, А, В (11.1) и элементам множества К и Q (11.2). Для решения задач логического моделирования в формальной системе применяются методы исчисления высказываний и методы исчисления предикатов.