Продольные волны в твёрдом теле. Волновое уравнение.

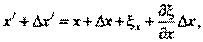
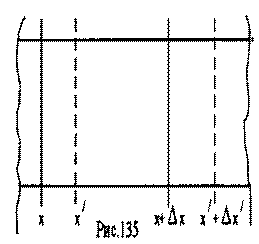
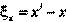В твёрдом теле, в котором распространяется продольная волна в направлении оси ОХ, выделим стержень сечения S₀, ось которого совпадает с направлением распространения волны. В стержне выделим небольшой участок между сечениями, имеющими координаты х и x+Δx (рис.135). При распространении волны стержень деформируется, и координаты граничных сечений выделенного участка изменяются. Пусть к моменту времени t + Δt координата левого сечения участка равна х', тогда смещение этого сечения за промежуток времени Δt равно . Правое граничное сечение участка к моменту времени t + Δt имеет координату

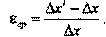
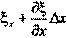а его смещение за промежуток времени Δt равно , средняя же относительная деформация, равная отношению удлинения к первоначальной длине

Истинной относительной деформацией, или относительной деформацией в точке называется предел, к которому стремится значение средней деформации при Δx→ 0,

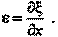т.е.

Следует различать смещение и деформации. Например, смещение в данной точке отсутствует, равно нулю. В то же время две соседние плоскости по обе стороны от выделенного сечения могут или приблизиться или отдаляться от него, т.е. деформация отлична от нуля. Наоборот, если соседние плоскости имеют одинаковые смещения, деформация участка среды между ними равна нулю.

Для вывода уравнения, описывающего волновой процесс, так называемого волнового уравнения, применим второй закон Ньютона к выделенному участку стержня. Если плотность вещества равна ρ₀, то масса выделенного участка равна ρ₀S₀Δx. Движение участка происходит под действием сил упругости, приложенных к его торцам. Равнодействующая сил упругости равна (ρ_x+Δx – ρ_x) S₀, где ρ_x и ρ_x+Δx - напряжения в торцевых сечениях. По второму закону динамики

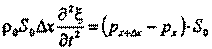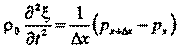Разделив обе части уравнения на объём участка, получим, что

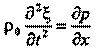Переходя к пределу при Δx→ 0, получаем уравнение:

которое справедливо для любой точки. Уравнение показывает, что ускорение данной точки среды пропорционально распределению деформации вдоль направления распространения волны. Выражая напряжение из закона Гука через относительную деформацию, получим:

Это и есть волновое уравнение. Из него видно, что смещение частиц среды может распространяться вдоль стержня в виде упругих волн ξ = asin(ωt - kx) или ξ = asin(ωt + kx). Уравнению (423) будет также удовлетворять и суперпозиция таких волн. Уравнение плоской волны, полученное ранее, является решением волнового уравнения. Таким образом, волновому уравнению (423) удовлетворяют синусоидальные волны. Более того, если волновому уравнению удовлетворяют синусоидальные волны различных частот, то и их суперпозиция также удовлетворяет волновому уравнению, т.е. косинусоидальная волна также может рассматриваться как решение приведенного волнового уравнения.

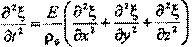Рассматривая аналогичным образом волну, движущуюся в произвольном направлении в пространстве, можно получить волновое уравнение в виде: