Сложение взаимно перпендикулярных колебаний.
В результате сложения взаимноперпендикулярных колебаний получаются сложные в общем случае по виду траектории движения. Поэтому мы рассмотрим частный случай, когда складываемые колебания имеют одинаковые частоты, но разные амплитуды и фазы. В этом случае отдельные составляющие можно записать в виде 
и 
. Здесь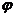 
- сдвиг фаз между складываемыми колебаниями.
Для определения вида траектории результирующего движения из закона движения следует исключить время. Для этого из первого выражения значение гармонической функции подставим во второе. Тогда получим, что:
Для удобства последующего анализа выражение лучше представить в форме:
Даже в этом простом случае уравнение траектории для произвольного сдвига фаз между отдельными колебаниями принимает сложный вид. Мы рассмотрим частные случаи сдвига фаз.
а) 
. При таком сдвиге фаз уравнение траектории принимает вид
Упрощая выражение, получаем, что 
т.е. траектория представляет собой прямую линию, которая лежит в первом и третьем квадрантах.
б) 
. При таком сдвиге фаз уравнение траектории преобразуется к виду
.
Отсюда следует, что 
, т.е. и в этом случае траектория представляет собой прямую линию с тем же наклоном, но она лежит уже во втором и четвёртом квадрантах.
в) 
. Уравнение траектории для такого сдвига фаз имеет вид
,
т.е. представляет собой эллипс. Следует заметить, что как при сдвиге фаз 
, так и при 
уравнение траектории имеет один и тот же вид. Но характер движения точки вдоль своей траектории будет различным. В начальный момент времени 
смещение вдоль оси X равно нулю, а вдоль оси Y +b и -b соответственно. При дальнейшем движении точки по траектории смещение вдоль X увеличивается и принимает положительные значения, т.е. точка движется по траектории вправо. Это означает, что при сдвиге фаз точка должна двигаться по направлению хода часовых стрелок, а при против хода. Таким образом, такое изменение фазы приводит к изменению направления движения вдоль траектории. Рассмотренный случай сложения взаимноперпендикулярных колебаний приведен на рис.108.
|
взаимноперпендикулярных колебаний одинаковой частоты
представляют собой только частный случай так называемых фигур Лиссажу. Фигурами Лиссажу называют траектории, описываемые точкой, совершающей одновременно два гармонических колебания во взаимноперпендикулярных направлениях. Вид таких траекторий
зависит от соотношения между частотами складываемых колебаний, между их фазами и амплитудами. Если частоты отдельных колебаний не совпадают, как в рассмотренном выше случае, то в общем случае разность фаз между колебаниями будет изменяться с течением времени, вследствие чего картина размывается, и фигуры Лиссажу не наблюдаются. Но если частоты складываемых колебаний относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в начальное положение, т.е. получаются устойчивые фигуры сложной формы. При этом число касаний фигурой Лиссажу сторон прямоугольника, в который она вписана, даёт отношение периодов складываемых колебаний (их частот).
Вид фигур Лиссажу позволяет определить соотношение между частотами колебаний и их фазами. Даже если колебания не являются гармоническими, характерные особенности фигуры Лиссажу сохраняются, искажается только её форма. Таким образом, по виду фигуры Лиссажу можно определить соотношение между частотами и фазами складываемых колебаний, а также оценивать, насколько сильно они отличаются от гармонических. На рис.109 приведены некоторые фигуры Лиссажу для различных соотношений между частотами складываемых колебаний и сдвига фаз между ними.
