Относительность механического движения.

Покой и движение тел относительны и определяются выбором тела отсчета (системы отсчета). Например, сидящий в вагоне движущегося поезда пассажир покоится относительно вагона и движется относительно полотна дороги.

Абсолютным называется движение тела относительно системы, условно принятой за неподвижную.

Система, совершающая движение относительно неподвижной системы, называется движущейся или подвижной.

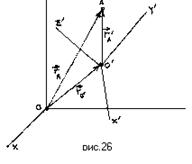
Относительным называется движение тела относительно подвижной системы. Переносным называется движение подвижной системы относительно неподвижной. Пусть положение т. А определено в двух системах отсчета: неподвижной OXYZ и подвижной O'X'Y'Z'

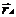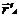
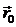неподвижной системе положение т. А определяются радиус-вектором в подвижной – , а положение начала подвижной системны относительно неподвижной определяются вектором .

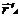
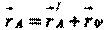
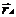Как видно из рисунка, связь между радиус-векторами и , определяющими положение точки в обеих системах отсчета выражается соотношением:

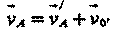Легко видеть, что аналогично связаны и векторы скорости в этих системах (абсолютная и относительная):

Но для вектора ускорения при произвольном движении тела и подвижной системы эта связь оказывается более сложной.

Если подвижная система наряду с поступательным совершает и вращательное движение, а тело движется относительно нее, в относительном и переносном ускорениях появляется дополнительный член, одинаковый и для относительного, и для переносного ускорения, обусловленный движением тела во вращающейся системе отсчета. Это происходит даже при равномерном движении тела относительно подвижной системы. Следовательно, с точки зрения наблюдателя подвижного, нарушается основной закон динамики (т.е. подвижная система не попадает в круг систем, определенный первым законом Ньютона).

Системы, в которых выполняется законы Ньютона, называют инерциальными. Инерциальные - это такие системы отсчета, в которых ускорение вызывается только действием сил, а сами силы появляется только в результате взаимодействий тел.

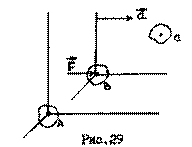Предположим, что две системы отсчета находятся в относительном движении (рис.29)

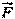Если тело С покоится относительно системы А, то оно движется равномерно и прямолинейно относительно подвижной системы, пока к телу отсчета В не приложены силы. Если же к телу отсчета В приложить силу , система начнет двигаться ускоренно относительно системы А и, соответственно. тело С относительно нее получит ускорение, хотя на него и не действуют силы. Основной закон динамики нарушается. Поэтому инерциальные системы отсчета связаны только со свободными телами отсчета.

16.2. Галилеевы преобразования координат и закон сложения скоростей.

Предположим, что одна из систем отсчета неподвижна, а другая - движется относительно первой с постоянной скоростью, так что оси ОХ,O’Х' и OY ,0'Y' остается параллельными, а ось 0'Y' скользит вдоль OY со скоростью (рис.30).

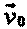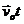Положение т. А можно задать векторным и координатным способами в обеих системах отсчета. Будем считать, что в исходный момент времени системы полностью совпадают. Тогда к моменту времени t, измеренному в неподвижной системе, подвижная система совершит перемещение . Координаты т. А в двух системах отсчета связаны соотношениями:

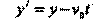х' = х (133)

z'=z (135)

Опыт показывает, что течение времени в обеих системах одинаково:

t'=t (136)

Совокупность соотношений (133, 134, 135, 136) и представляет собой преобразования Галилея в координатной форме.

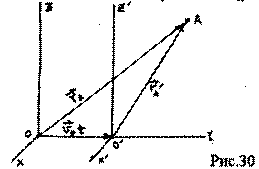
Более компактную форму принимают преобразования Галилея, если положение т. А определять векторным способом:

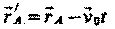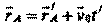t' = t Справедливы и преобразования Галилея для обратного перехода:

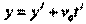х = х' z=z t=t’ t = t'

Скорость т. А в двух системах отсчета связана соотношением:
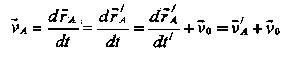