Вычисление приближенных значений.
Цель:научиться вычислять абсолютные и относительные погрешности приближений, находить границы погрешностей; выполнять действия над приближенными числами с учетом и без учета границ погрешностей.
Средства обучения:
- методические рекомендации к практической работе № 3.
Виды самостоятельной работы:
- нахождение погрешности приближения;
- вычисление абсолютной и относительной погрешности приближения;
- нахождение границ погрешностей приближений;
- нахождение суммы, разности приближенных значений с учетом границ погрешностей;
- нахождение произведения, частного приближенных значений с учетом границ погрешностей;
- выполнение арифметический действий над приближенными значениями без учета границ погрешностей.
Краткая теоретическая справка
Если результат измерения или вычисления величины x с некоторой точностью равен  , то
, то  называют приближенным значением (приближением) величины x.
называют приближенным значением (приближением) величины x.
Разность между точным и приближенным значениями величины называется погрешностью приближения 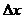 .
.
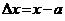
Модуль разности между точным и приближенным значениями величины называется абсолютной погрешностью приближения 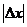 .
.
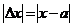
В случаях, когда неизвестно точное значение величины и из-за этого нельзя найти абсолютную погрешность приближения, указывают положительное число, больше которого абсолютная погрешность быть не может. Это число называют границей абсолютной погрешности.
Если  , то
, то  есть граница абсолютной погрешности.
есть граница абсолютной погрешности.
Тогда 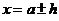 ,т.е. истинное значение величины x заключается в пределах
,т.е. истинное значение величины x заключается в пределах 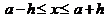 .
.
Для характеристики качества измерения используют понятие относительной погрешности. Отношение абсолютной погрешности приближения к модулю приближенного значения величины называется относительной погрешностью приближения.
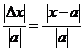
Любое положительное число, которое больше или равно относительной погрешности, называется границей относительной погрешности.
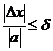 , где
, где  - граница относительной погрешности.
- граница относительной погрешности.
Если  - граница абсолютной погрешности, то граница относительной погрешности равна
- граница абсолютной погрешности, то граница относительной погрешности равна
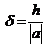 .
.
Если 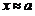 с точностью до
с точностью до 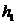 ,
, 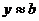 с точностью до
с точностью до 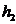 , то
, то  с точностью до
с точностью до 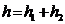 и
и 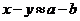 с точностью до
с точностью до 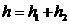 .
.
Если 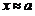 с относительной точностью до
с относительной точностью до  ,
, 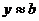 с относительной точностью до
с относительной точностью до 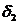 , то
, то 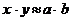 с относительной точностью до
с относительной точностью до 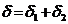 и
и  с относительной точностью до
с относительной точностью до 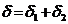 .
.
Если 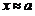 с относительной точностью до
с относительной точностью до  , то относительная точность приближенного равенства
, то относительная точность приближенного равенства 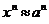 есть
есть  .
.
Граница относительной погрешности корня n-й степени в n раз меньше границы относительной погрешности подкоренного числа.
Практические задания для аудиторной работы
1. Найти погрешность, абсолютную и относительную погрешность приближенного значения  величины
величины  .
.
2. Определить точность приближенного равенства 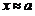 .
.
1.,2. а) 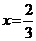 ;
; 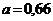 ; б)
; б)  ;
;  .
.
3. Определить относительную точность приближенного равенства 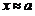 .
.
а) 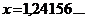 ;
;  ; б)
; б)  ;
; 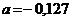 .
.
4. Найти периметр 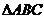 , если
, если 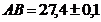 ,
,  ,
, 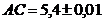 .
.
5. Вычислить чему равна площадь прямоугольника шириной 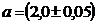 м и длиной
м и длиной 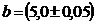 м.
м.
6. Вычислить периметр четырехугольника 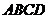 , если
, если  ,
, 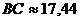 ,
, 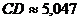 ,
, 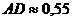 .
.
Практические задания для самостоятельной работы
Вариант 1
1.,2. а) 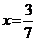 ;
; 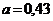 ; б)
; б) 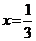 ;
;  .
.
3. а) 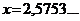 ;
; 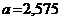 ; б)
; б)  ;
; 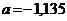 .
.
4. Найти разность 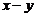 , если
, если 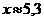 с точностью до 1%,
с точностью до 1%, 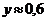 с точностью до 2%.
с точностью до 2%.
5. Вычислить 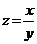 , если
, если  и
и 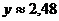 с точностью до 1%.
с точностью до 1%.
6. Найти произведение чисел 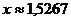 и
и  .
.
Вариант 2
1.,2. а)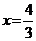 ;
; 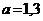 ; б)
; б)  ;
;  .
.
3. а)  ;
; 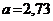 ; б)
; б) 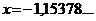 ;
; 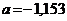 .
.
4. Найти периметр прямоугольника 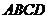 , если
, если  ,
, 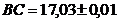 .
.
5. Вычислить площадь ромба 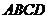 , если его диагонали равны
, если его диагонали равны 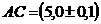 см,
см,  см.
см.
6. Вычислить периметр 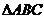 , если
, если 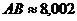 ,
,  ,
, 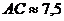 .
.
Вариант 3
1.,2. а) 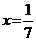 ;
;  ; б)
; б) 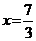 ;
; 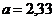 .
.
3. а)  ;
; 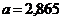 ; б)
; б)  ;
;  .
.
4. Найти разность 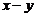 , если
, если 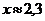 с точностью до 0,1%,
с точностью до 0,1%, 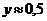 с точностью до 1%.
с точностью до 1%.
5. Вычислить чему равна площадь прямоугольника шириной 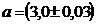 м и длиной
м и длиной 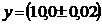 м.
м.
6. Найти произведение чисел 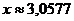 и
и  .
.
Вариант 4
1.,2. а)  ;
; 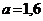 ; б)
; б)  ;
; 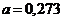 .
.
3. а) 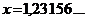 ;
; 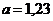 ; б)
; б)  ;
; 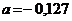 .
.
4. Найти периметр прямоугольника 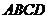 , если
, если 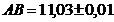 ,
, 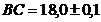 .
.
5. Вычислить площадь ромба 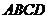 , если его диагонали равны
, если его диагонали равны  см,
см, 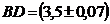 см.
см.
6. Вычислить периметр 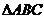 , если
, если 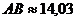 ,
,  ,
, 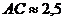 .
.
Требования к отчёту:
1. После выполнения работы студент обязан продемонстрировать преподавателю выполненные задания.
2. Предоставить отчёт о выполненной работе, содержащей:
- порядковый номер и наименование практической работы;
- цель практической работы;
- ход выполнения работы;
- ответы на контрольные вопросы;
- вывод о выполненном задании.
Контрольные вопросы
1. Что называют погрешностью приближения?
2. Что такое абсолютная погрешность приближения?
3. Какую погрешность называют относительной?
4. Что называют границами абсолютной и относительной погрешностей?
5. Какая существует связь между абсолютной и относительной погрешностями?
6. Чему равна погрешность суммы и разности приближенных значений?
7. Как вычислить погрешность произведения и частного приближенных значений?
8. Что такое верные и строго верные числа в записи приближенных значений?
9. Какие цифры в записи приближенного значения называют значащими?
10. Какими правилами пользуются при вычислениях без учета границ погрешностей?
Сделайте вывод о том, какие математические навыки вы приобрели на этом занятии.
Практическая работа № 4
Преобразование и вычисление числовых значений алгебраических выражений, содержащих степени с рациональными показателями
Цель:научиться применять свойства степени для преобразования степенных выражений.
Средства обучения:
- методические рекомендации к практической работе № 4.
Виды самостоятельной работы:
- вычисление значения выражения с применением свойств степени;
- решение уравнений;
- упрощение буквенных выражений с применением свойств степени.
Краткая теоретическая справка
Степенью числа a с натуральнымпоказателем n, большим 1, называется произведение n множителей, каждый из которых равен a:
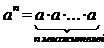 .
.
Если 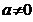 , (
, ( 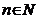 ), то
), то 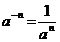 .
.
Если 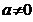 , то
, то 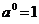 .
.
Свойства степени
1. 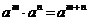 ;
;
2. 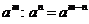 ;
;
3. 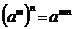 ;
;
4. 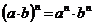 ;
;
5. 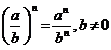 .
.
Практические задания
1. Найти значение выражения, используя свойства степени.
2. Решите уравнение.
3. Упростить выражение.
Для аудиторной работы
1. а) 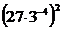 ; б)
; б) 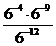 ; в)
; в) 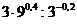 .
.
2. а) 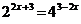 ; б)
; б) 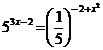 .
.
3. а) 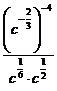 ; б)
; б) 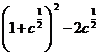 ; в)
; в) 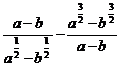 .
.
Для самостоятельной работы
Вариант 1
1. а) 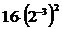 ; б)
; б) 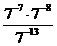 ; в)
; в) 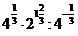 .
.
2. а) 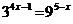 ; б)
; б) 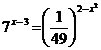 .
.
3. а) 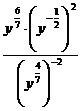 ; б)
; б) 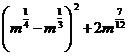 ; в)
; в) 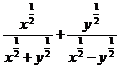 .
.
Вариант 2
1. а) 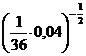 ; б)
; б) 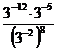 ; в)
; в) 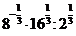 .
.
2. а) 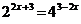 ; б)
; б) 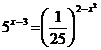 .
.
3. а) 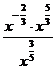 ; б)
; б) 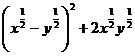 ; в)
; в) 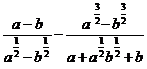 .
.
Вариант 3
1. а) 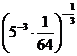 ; б)
; б) 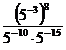 ; в)
; в) 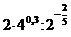 .
.
2. а) 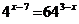 ; б)
; б) 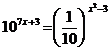 .
.
3. а) 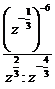 ; б)
; б) 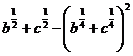 ; в)
; в) 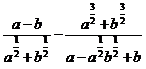 .
.
Вариант 4
1. а) 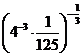 ; б)
; б) 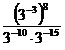 ; в)
; в) 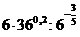 .
.
2. а) 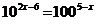 ; б)
; б) 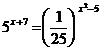 .
.
3. а) 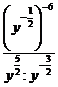 ; б)
; б) 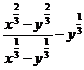 ; в)
; в) 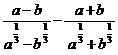 .
.
Требования к отчёту:
1. После выполнения работы студент обязан продемонстрировать преподавателю выполненные задания 1-3.
2. Предоставить отчёт о выполненной работе, содержащей:
- порядковый номер и наименование практической работы;
- цель практической работы;
- ход выполнения работы;
- ответы на контрольные вопросы;
- вывод о выполненном задании.
Контрольные вопросы
1. Выражение какого вида называют степенью?
2. Что понимают под 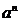 , где n – натуральное число?
, где n – натуральное число?
3. Что понимают под 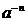 , где
, где 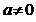 и n – натуральное число?
и n – натуральное число?
Сделайте вывод о том, какие математические навыки вы приобрели на этом занятии.
Практическая работа № 5
Преобразование и вычисление числовых значений алгебраических
выражений, содержащих корни n-ой степени ( 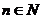 )
)
Цель:научиться выполнять преобразования и находить значения выражений, содержащих корни n-й степени.
Средства обучения:
- методические рекомендации к практической работе № 5.
Виды самостоятельной работы:
- вычисление значения корня n-й степени;
- извлечение корня из произведения и частного;
- извлечение корня из корня;
- возведение корня в степень.
Краткая теоретическая справка
Корнем n-й степени из числа 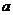 называется такое число, n-я степень которого равна
называется такое число, n-я степень которого равна 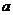 .
.
Обозначается 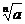 , где
, где 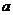 - подкоренное выражение (или число), n - показатель корня (
- подкоренное выражение (или число), n - показатель корня ( 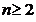 ;
; 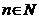 ).
).
По определению 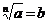 , если
, если 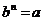 или
или 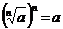 .
.
Основные свойства арифметического корня n-й степени
1) Корень из произведения:
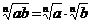 ,
,
где 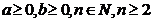 .
.
2) Корень из дроби:
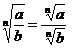 ,
,
где 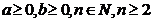 .
.
3) Возведение корня в степень:
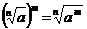 ,
,
где 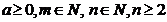 .
.
4) Извлечение корня из корня:
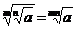 ,
,
где 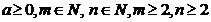 .
.
5) Если показатели корня и подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится. 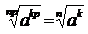 .
.
Практические задания
1. Найти значение выражения, используя свойства корня из произведения и из частного.
2. Вычислить, используя свойства извлечения корня из корня.
3. Преобразовать и найти значение выражения с применением свойства возведения корня в степень.
4. Решить уравнение.
Для аудиторной работы
1. а) 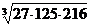 ; б)
; б) 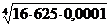 ; в)
; в) 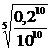 ; г)
; г) 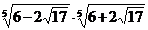 .
.
2. а) 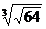 ; б)
; б) 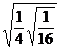 .
.
3. а) 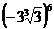 ; б)
; б) 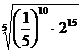 .
.
4. а) 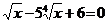 ; б)
; б) 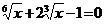 .
.
Для самостоятельной работы
Вариант 1
1. а) 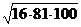 ; б)
; б) 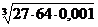 ; в)
; в) 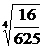 ; г)
; г) 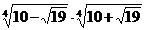 .
.
2. а) 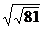 ; б)
; б) 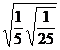 .
.
3. а) 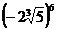 ; б)
; б) 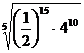 .
.
4. а) 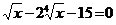 ; б)
; б) 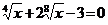 .
.
Вариант 2
1. а) 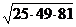 ; б)
; б) 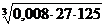 ; в)
; в) 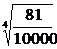 ; г)
; г) 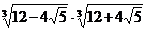 .
.
2. а) 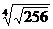 ; б)
; б) 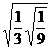 .
.
3. а) 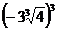 ; б)
; б) 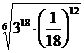 .
.
4. а) 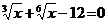 ; б)
; б) 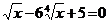 .
.
Вариант 3
1. а) 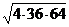 ; б)
; б) 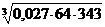 ; в)
; в) 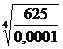 ; г)
; г) 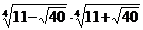 .
.
2. а) 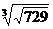 ; б)
; б) 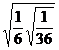 .
.
3. а) 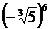 ; б)
; б) 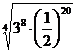 .
.
4. а) 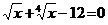 ; б)
; б) 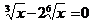 .
.
Вариант 4
1. а) 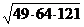 ; б)
; б) 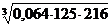 ; в)
; в) 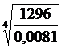 ; г)
; г) 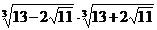 .
.
2. а) 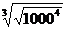 ; б)
; б) 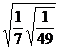 .
.
3. а) 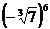 ; б)
; б) 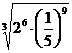 .
.
4. а) 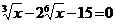 ; б)
; б) 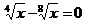
Требования к отчёту:
1. После выполнения работы студент обязан продемонстрировать преподавателю выполненные задания 1-4.
2. Предоставить отчёт о выполненной работе, содержащей:
- порядковый номер и наименование практической работы;
- цель практической работы;
- ход выполнения работы;
- ответы на контрольные вопросы;
- вывод о выполненном задании.
Контрольные вопросы
1. Что называют корнем n-й степени из действительного числа?
2. Может ли корень четной степени из положительного числа быть отрицательным?
3. При каком условии можно извлечь корень n-й степени из отрицательного числа?
4. Как называется корень n-й степени, если n=2, n=3?
5. Свойства корня n-й степени.
Сделайте вывод о том, какие математические навыки вы приобрели на этом занятии.
Практическая работа № 6
Преобразование и вычисление числовых значений алгебраических выражений, содержащих степени и корни
Цель:научиться применять свойства степени и корня для преобразования алгебраических выражений.
Средства обучения:
- методические рекомендации к практической работе № 6.
Виды самостоятельной работы:
- сравнение выражений;
- вычисление значения выражения с применением свойств степени и корня;
- упрощение буквенных выражений с применением свойств степени и корня;
- решение уравнений графическим способом;
- решение уравнений путем введения новой переменной.
Краткая теоретическая справка
Если 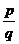 - обыкновенная дробь (
- обыкновенная дробь ( 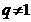 ) и
) и 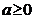 , то под
, то под 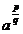 понимают
понимают 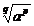 :
:
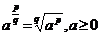 .
.
Если 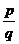 - обыкновенная дробь (
- обыкновенная дробь ( 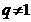 ) и
) и 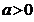 , то под
, то под 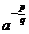 понимают
понимают 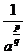 :
:
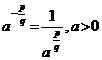 .
.
Для степени с рациональным показателем справедливы те же свойства, что и для степени с целым показателем.
Пусть a > 0, b > 0, r, s − любые рациональные числа. Тогда степень с любым рациональным показателем обладает следующими свойствами.
1. ar · as = ar + s.
2. ar : as = ar – s.
3. (ar)s = ars.
4. (ab)r = ar · br .
5. 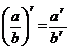 .
.
Практические задания
1. Расположить числа в порядке возрастания.
2. Найти значение выражения.
3. Упростить выражение.
Для аудиторной работы
1. а) 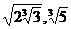 и
и 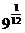 ; б)
; б) 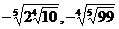 и
и 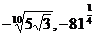 .
.
2. а) 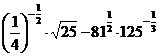 ; б)
; б) 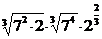 ; в)
; в) 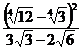 .
.
3. а) 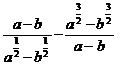 ; б)
; б) 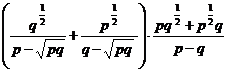 .
.
Для самостоятельной работы
Вариант 1
1. а) 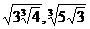 и
и 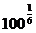 ; б)
; б) 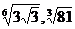 и
и 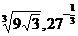 .
.
2. а) 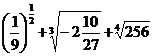 ; б)
; б) 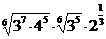 ; в)
; в) 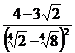 .
.
3. а) 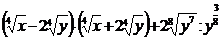 ; б)
; б) 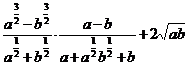 .
.
Вариант 2
1. а) 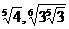 и
и 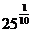 ; б)
; б) 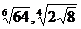 и
и 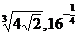 .
.
2. а) 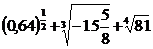 ; б)
; б) 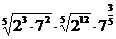 ; в)
; в) 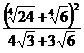 .
.
3. а) 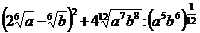 ; б)
; б) 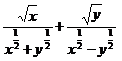 .
.
Вариант 3
1. а) 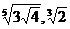 и
и 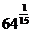 ; б)
; б) 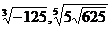 и
и 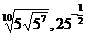 .
.
2. а) 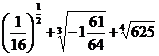 ; б)
; б) 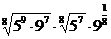 ; в)
; в) 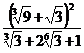 .
.
3. а) 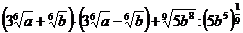 ; б)
; б) 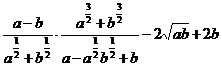 .
.
Вариант 4
1. а) 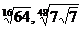 и
и 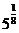 ; б)
; б) 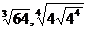 и
и 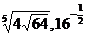 .
.
2. а) 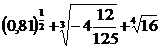 ; б)
; б) 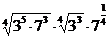 ; в)
; в) 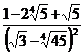 .
.
3. а) 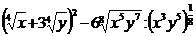 ; б)
; б) 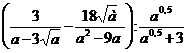 .
.
Требования к отчёту:
1. После выполнения работы студент обязан продемонстрировать преподавателю выполненные задания 1-3.
2. Предоставить отчёт о выполненной работе, содержащей:
- порядковый номер и наименование практической работы;
- цель практической работы;
- ход выполнения работы;
- ответы на контрольные вопросы;
- вывод о выполненном задании.
Контрольные вопросы
1. Что называют корнем n-й степени из действительного числа?
2. Свойства корня n-й степени.
3. Что понимают под 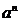 , где n – натуральное число?
, где n – натуральное число?
4. Что понимают под степенью с дробным показателем?
5. Что понимают под 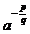 , где
, где 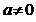 ?
?
6. Свойства степени с действительным показателем.
Сделайте вывод о том, какие математические навыки вы приобрели на этом занятии.
Практическая работа № 7
