Тема: Объемы многогранников и тел вращения
Цели:
– научиться выполнять чертеж к задаче;
– научиться находить объем прямоугольного параллелепипеда.
Оснащение занятия: учебник, конспект, плакат, модель.
Порядок выполнения работы
Задание 1. Вопросы для повторения.
1. Что называется, прямоугольным параллелепипедом? (указать модель).
2. Что называют измерениями прямоугольного параллелепипеда?
3. Чему равен квадрат диагонали прямоугольного параллелепипеда?
4. Сформулируйте теорему об объеме прямоугольного параллелепипеда.
5. Сформулируйте следствия, вытекающие из этой теоремы.
6. Какой прямоугольный параллелепипед называется кубом? (указать модель).
7. Чему равен объем куба?
Задание 2. Решите задачу: Дан прямоугольный параллелепипед с основанием квадрат. Вычислить объем параллелепипеда, если его высота равна 10см, периметр основания 16см.
Задание 3. Выполните № 658, № 649(а), № 652, № 650.
Контроль знаний студентов:
проверить практическую работу;
самостоятельная работа по 2-м вариантам.
Вариант 1.
1. Выполните № 648(б).
2. Найдите объем прямоугольного параллелепипеда, если его длина равна 6см, ширина – 7см, а диагональ – 11см.
Вариант 2.
1. Выполните № 648(г).
2. Найдите объем прямоугольного параллелепипеда, если его длина равна 2см, ширина – 6см, а диагональ – 17см.
Литература: Атанасян Л. С. Геометрия стр.148.
Практическая работа № 8
Тема: Действия над векторами
Цели:
научиться определять вектор суммы и разности нескольких векторов;
научиться применять координатный метод к решению задач.
Оснащение занятия: учебник, конспекты, плакаты.
Порядок выполнения работы
Задание 1. Повторите теоретический материал п.34-п.35 стр.81 и
выполните: 1) №321(а, б – по одному вектору), 2) дайте ответ на вопрос 1 стр.96.
Задание 2. Какие действия можно выполнять над векторами? Повторите п.36-п.37 стр.84. Какие векторы называются компланарными? Повторите п.39. Выполните №327(а; б), №331(а), №330(а; в; д), №382, №355(а ;г)
Задание 3. Повторите правила, позволяющие по координатам данных векторов найти координаты их суммы, разности и произведение вектора на число (п.43 стр.102). Выполните №410(1).
Задание 4. Повторите формулы, которые применяются при решении задач в координатах (п.45 стр.104) и выполните №429, №431(а; в).
Задание 5. Повторите п.46-п.48 стр.110. Скалярное произведение векторов. Выполните №444(1;5), №446(а;б), №448(а), №451(а), №464(а).
Контроль знаний студентов:
– Проверить практическую работу студентов.
– Контрольные вопросы: стр.96 №6-№9, №11, №14. стр.121 №4, №7, №11, №12, №13.
Литература: Атанасян Л. С. Геометрия стр. 84, стр.104.
Практическая работа № 9
Тема: Нахождение значений числовых выражений
Цели: овладеть практическими навыками выполнения арифметических действий над числами.
Задачи: -повторить теорию о арифметических действиях над числами
- закрепить материал по арифметическим действиям над числами
Средства обучения: учебник, карточки-задания
Методы обучения: практический
Теоретическое обоснование:
Арифметическое действие – это нахождение по данным числам одного нового числа.
Возьмём, например, число 7. Прибавим к нему единицу, получим новое число 8. Отнимем от 7 единицу, получим новое число 6.
Таким образом мы из двух данных чисел 7 и 1 составили два новых числа: 8 и 6, то есть произвели арифметические действия.
Прибавление к числу одной единицы называется простым счётом, вычитание из числа одной единицы называется обратным счётом.
Если арифметическое действие производится над двумя числами, то оно называется простым. Если данных чисел более двух, то действие называется сложным.
Основных арифметических действий четыре: сложение, вычитание, умножение и деление.
Правило нахождения наибольшего общего делителя (НОД).
Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
3) найти произведение оставшихся множителей.
Правило нахождения наименьшего общего кратного (НОК).
Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) выписать множители, входящие в разложение одного из чисел;
3) добавить к ним недостающие множители из разложений остальных чисел;
4) найти произведение получившихся множителей.
Содержание работы
Вариант 1
1.Найти НОД и НОК чисел:
а) 154 и 210б) 255 и 510
2. Найдите остаток отделения на 3 числа:
а) 1 234 321; б) 55 555;в)155 555
3. Записать в виде десятичной дроби
а) 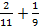 ; б)
; б) 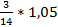
4. Сравните числовые значения выражений:  ;
;
5. Вычислить: а) 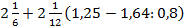
б) 400 · 8 – 2000 : 20 + 450
в) (3212 : 44 + 14) · 61
6. Вычислить: 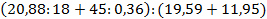
Вариант 2
1.Найти НОД и НОК чисел:
а) 120 и 144б) 105 и 165
2. Найдите остаток отделения на 9 числа:
а) 1 234 567; б) 55 555;в)155 555
3. Записать в виде десятичной дроби
а) 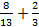 ; б)
; б) 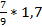
4. Сравните числовые значения выражений: 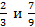
5. Вычислить: 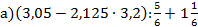
б) (8007 + 32415) : 3 · 10
в) 64 · 10 – (26000 : 100) + 234
6. Вычислить: 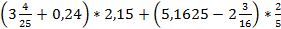
Вариант 3
1.Найти НОД и НОК чисел:
а) 75 и 60 б) 48 и 36
2. Найдите остаток отделения на 3 числа:
а) 1 234 321; б) 55 555; в)155 555
3. Записать в виде десятичной дроби
а) 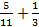 ; б)
; б) 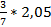
4. Сравните числовые значения выражений: 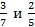 ;
;
5. Вычислить: а) 
б) 400 · 8 – 2000 : 20 + 450
в) (3212 : 44 + 14) · 61
6. Вычислить: 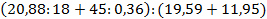
Вариант 4
1.Найти НОД и НОК чисел:
а) 72 и 128 б) 15 и 33
2. Найдите остаток отделения на 9 числа:
а) 1 234 567; б) 55 555; в)155 555
3. Записать в виде десятичной дроби
а) 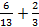 ; б)
; б) 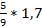
4. Сравните числовые значения выражений: 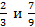
5. Вычислить: 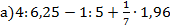
б) (8007 + 32415) : 3 · 10
в) 64 · 10 – (26000 : 100) + 234
6. Вычислить: 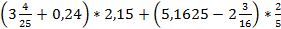
Практическая работа № 10
