МИНОБРНАУКИ Челябинской области

МИНОБРНАУКИ Челябинской области

государственное бюджетное профессиональное образовательное учреждение

«Южноуральский энергетический техникум»

ГБПОУ ЮЭТ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

По выполнению практических работ

учебная дисциплина «Математика: алгебра, начала математического анализа, геометрия»

Для профессии: 43.02.15 «Поварское, кондитерское дело»

Составитель: О.М. Гаранина

Содержание

Пояснительная записка. 4

Перечень практических работ. 5

Практическая работа № 1-Тема: Взаимное расположение прямых и плоскостей. 6

Практическая работа № 2-Тема: Призма. 7

Практическая работа № 3-Тема: Пирамида. 8

Практическая работа№ 4-Сечения в призме и пирамиде. 10

Практическая работа № 5-Тема: Цилиндр. 12

Практическая работа № 6-Тема: Конус, шар и сфера. 13

Практическая работа № 7-Тема: Объемы многогранников и тел вращения. 14

Практическая работа № 8-Тема: Действия над векторами. 15

Практическая работа № 9-Тема: Нахождение значений числовых выражений. 16

Практическая работа № 10-Тема: Решение рациональных уравнений. 18

Практическая работа № 11-Тема: Решение рациональных неравенств. 20

Практическая работа № 12-Тема: Исследование свойств функции. 22

Практическая работа № 13-Тема: Преобразование графиков функций. 23

Практическая работа № 14-Тема: Преобразование иррациональных выражений. 26

Практическая работа № 15-Тема: Решение иррациональных уравнений. 27

Практическая работа № 16-Тема: Решение иррациональных неравенств. 28

Практическая работа № 17-Тема: Степень с рациональным показателем.. 31

Практическая работа №18-Тема: Решение показательных уравнений. 35

Практическая работа №19-Тема: Решение показательных неравенств. 36

Практическая работа №20-Тема: Логарифм и его свойства. 37

Практическая работа № 21-Тема: Решение логарифмических уравнений. 39

Практическая работа №22-Тема: Решение логарифмических неравенств. 40

Практическая работа № 23-Тема: Синус, косинус, тангенс и котангенс числа. 41

Практическая работа №24-Тема: Основные тригонометрические тождества. 42

Практическая работа № 25-Тема: преобразование графиков тригонометрических функций. 43

Практическая работа № 26-Тема: Формулы тригонометрии. 44

Практическая работа № 27-Тема: Преобразование суммы тригонометрических выражений в произведение 45

Практическая работа № 28-Тема: Тригонометрические уравнения. 47

Практическая работа № 29-Тема: Методы решения тригонометрических уравнений. 48

Практическая работа № 30-Тема: Вычисление пределов. 49

Практическая работа № 31-Тема: Производная функции. 52

Практическая работа № 32-Тема: исследование функции с помощью производной. 53

Практическая работа № 33-Тема: Первообразная. 54

Практическая работа № 34-Тема: Вычисление площадей плоских фигур. 55

Практическая работа № 35-Тема: Комбинаторика. 56

Практическая работа № 36-Тема: Вычисление вероятностей. 57

Практическая работа № 37-Тема: Дискретная случайная величина. 59

Практическая работа № 38-Тема: Основные методы решения неравенств. 60

Практическая работа № 39-Тема: Основные методы решения систем уравнений. 62

Практическая работа № 40-Тема: Основные методы решения систем уравнений. 63

Пояснительная записка

Методические рекомендации по выполнению практических заданий по дисциплине «Математика: алгебра, начала математического анализа, геометрия», разработаны в помощь студентам для самостоятельного выполнения ими практических работ и подготовки к семинарским занятиям, предусмотренных рабочей программой.

Практические занятия проводятся после изучения соответствующих разделов и тем учебной дисциплины. Работы выполняются по индивидуальным заданиям. Так как учебная дисциплина имеет прикладной характер, то выполнение студентами практических работ позволяет им понять, где и когда изучаемые теоретические положения, и практические умения могут быть использованы в будущей практической деятельности.

Целью практических занятий является закрепление теоретических знаний и приобретение практических умений и навыков.

Методические рекомендации по каждой практической работе имеют теоретическую часть, с необходимыми для выполнения работы, формулами, пояснениями, таблицами; алгоритм выполнения заданий.

В результате выполнения практических работ студент долженуметь:

-работать с нормативной документацией предприятий общественного питания:

– применять требования нормативных документов к основным видам продукции (услуг) и процессов.

Перечень практическихработ

№	Тема практической работы	Кол-во часов
	Взаимное расположение прямых и плоскостей.
	Призма
	Пирамида
	Сечения в призме и пирамиде
	Цилиндр
	Конус, шар и сфера
	Объемы многогранников и тел вращения
	Действия с векторами
	Нахождение значений числовых выражений
	Решение рациональных уравнений
	Решение рациональных неравенств
	Исследование свойств функции
	Преобразования графиков функций
	Преобразование иррациональных выражений
	Решение иррациональных уравнений
	Решение иррациональных неравенств
	Степень с рациональным показателем
	Решение показательных уравнений
	Решение показательных неравенств
	Логарифм и его свойства
	Решение логарифмических уравнений
	Решение логарифмических неравенств
	Синус, косинус, тангенс и котангенс числа
	Основные тригонометрические тождества
	Преобразование графиков тригонометрических функций
	Формулы тригонометрии
	Преобразование суммы тригонометрических функций в произведение
	Тригонометрические уравнения
	Методы решения тригонометрических уравнений
	Вычисление пределов
	Производная функции
	Исследование функции с помощью производной
	Первообразная
	Вычисление площадей плоских фигур
	Комбинаторика
	Вычисление вероятностей
	Дискретная случайная величина
	Основные методы решения неравенств
	Основные методы решения систем уравнений
	Основные методы решения систем неравенств

Практическая работа № 1

Практическая работа № 2

Тема: Призма

Цели:

– научиться строить чертежи к задачам;

– научиться находить основные элементы призмы, пирамиды;

– научиться находить площадь полной и боковой поверхности призмы и пирамиды.

Оснащение занятия: учебник, конспекты, плакаты, модели многогранников.

Порядок выполнения работы:

Задание 1. Повторите учебный материал, необходимый для дальнейшей работы.

Вопросы для повторения I группе:

1. Среди многогранников выберите те, которые являются призмой.

2. Что называется, призмой? Дайте определения граням, ребрам и вершинам призмы (все элементы указать на плакате).

3. Какая призма называется прямой? (изобразить).

4. Чему равна боковая поверхность прямой призмы?

Вопросы для повторения II группе:

1. Что называется, параллелепипедом и является ли он призмой?

2. Начертите параллелепипед, обозначьте его и запишите формулы для нахождения площади полной и боковой поверхностей.

3. Какая призма называется правильной?

4. Какая призма называется наклонной?

Вопросы для повторения III группе:

1. Среди многогранников выберите те, которые являются пирамидой.

2. Что называется, пирамидой? Дайте определения граням, ребрам и высоте пирамиды (все элементы указать на плакате).

3. Начертите пирамиду, обозначьте ее и запишите формулы для нахождения площади полной и боковой поверхностей.

4. Что называется, усеченной пирамидой? Чему равны боковая и полная ее поверхности?

Вопросы для повторения IV группе:

1. Какая пирамида называется правильной? (выбрать нужную модель)

2. Что можно сказать о боковых ребрах и боковых гранях правильной пирамиды?

3. Что такое апофема правильной пирамиды?

4. Чему равна площадь боковой поверхности правильной пирамиды?

Задание 2. Решить задачи.

1. В прямой треугольной призме – основание прямоугольный треугольник с катетами 12см и 35см. Боковое ребро призмы 24см. Найдите площадь полной поверхности призмы.

2. Выполните № 219, № 223.

3. Основанием правильной пирамиды является четырехугольник со стороной 3см. Высота боковой грани 9см. Найдите площадь боковой и полной поверхностей пирамиды.

4. Выполните № 239, № 310.

Контроль знаний студентов:

Проверить практическую работу.

Вариант 1. №229(а), № 243. Вариант 2. № 229(б), № 244.

Литература: Атанасян Л. С. Геометрия стр.60-65.

Практическая работа № 3

Тема: Пирамида

Цель:закрепление понятий: пирамида, объем, площадь боковой и полной поверхности пирамиды.

Оборудование:модели пирамид, таблица с формулами S_б.п., S_п.п., V, линейки, карандаши, калькулятор, карточки вопрос - ответ (из истории пирамид), плакат с изображением египетских пирамид, диск «Энциклопедия», тесты приложение

Порядок выполнения работы

1. Ознакомиться с указаниями к выполнению практической работы

2. Сделать краткий конспект теоретического материала в рабочих тетрадях (основные понятия, определения, формулы, примеры)

3.Изучить условие заданий для практической работы.

4. Оформить отчет о работе.

Теоретический материал

Пирами́да — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д.

наклонная прямая

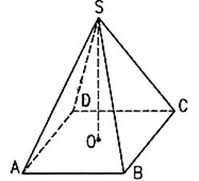
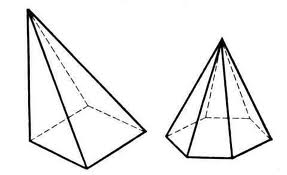Правильная пирамида

Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами: боковые ребра правильной пирамиды равны; в правильной пирамиде все боковые грани — равные равнобедренные треугольники; в любую правильную пирамиду можно как вписать, так и описать около неё сферу;

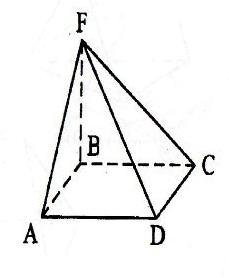Прямоугольная пирамида

Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.

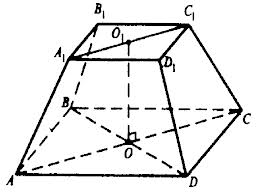Усечённая пирамида

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

Боковая поверхность — это сумма площадей боковых граней.

Для нахождения боковой поверхности в правильной пирамиде можно использовать формулу:

S_б.п.= 1/2•Р•ℓ

Полная поверхность — это сумма площади боковой поверхности и площади основания.

Для нахождения полной поверхности в правильной пирамиде можно использовать формулу:

S_п.п. = 1/2•Р•ℓ+S_осн.

Сечения пирамиды:

Ход работы:

1.Для нахождения площади боковой поверхности пирамиды нужно измерить линейкой следующие элементы: апофему, стороны основания, высоту. Подставить значения в формулу для нахождения пощади (если пирамида правильная). Если пирамида наклонная, то боковую поверхность находим из суммы площадей граней.

2. Для нахождения площади полной поверхности пирамиды нужно найти площадь основания пирамиды (площадь треугольника, прямоугольника, ромба)

3.Площадь полной поверхности пирамиды находиться как сумма площадей боковой поверхности и основания.

4. Для нахождения объема нужно знать высоту пирамиды и площадь основания.

Оформление работы:

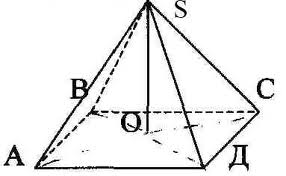	Дано: SАВСД – пирамида, АВ=3см, ВС= 6см, пирамида неправильная, Н=10см, ℓ1=10,5см., ℓ2=10,2см Найти: Sб.п. ;Sп.п. ; V Решение: т.к. пирамида неправильная, то Sб.п. находят как сумму площадей ее боковых граней, т.е. площадей треугольников. S1 = 1/2 ·ℓ1·АВ=1/2·10,5·3=15,75(см2) - это площадь одной грани, а их две одинаковых, т.е S1,2 =15,75·2=31,5(см2)
S3=1/2·ℓ2·ВС= 1/2·10,2·6=30,6 (см2), S3,4=2·30,6=61,2(см2) Sб.п.= 31,5+61,2 =92,7(см2) Sосн.= АВ·ВС=3·6=18(см2), Sп.п.= Sб.п+ Sосн.= 92,7+18=110,7 (см2) (если пирамида правильная, то пользуемся формулами) V=1/3· Sосн·Н = 1/3·18·10 = 60(см3) – формула объема справедлива для любой пирамиды. 5. Выполняют тесты, состоящие из двух вопросов и двух задач.

Задания для самостоятельной работы:

Вариант 1

1. Сколько ребер у шестиугольной пирамиды:

Ответ: а)6; б)12; в)18; г)24; д)8

2. Какое наименьшее число граней может иметь пирамида:

Ответ: а)5; б)12); в)10; г)6; д)4

3.Выберите верное утверждение:

а) Многогранник, составленный из n-треугольников, называется пирамидой;

б) пирамида называется правильной, если ее основание – правильный многоугольник;

в) высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой;

4. В правильной четырехугольной пирамиде высота равна 4см, а длина диагонали основания - 6 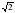см. Найдите площадь полной поверхности пирамиды.

Ответ: а)96см²; б)156см²; в)36см²; г)60см²; д)150см²

Вариант 2

1. Сколько граней у шестиугольной пирамиды:

Ответ: а)6; б)7; в)8; г)10; д)12

2. Какое наименьшее число ребер может иметь пирамида:

Ответ: а)6; б)5; в)4; г)7; д)8

3.Выберите верное утверждение:

а) Высота пирамиды называется высотой грани;

б) площадь боковой поверхности пирамиды равна произведению периметра основания на высоту;

в) пирамида называется правильной, если ее основание – правильный многоугольник;

4. Высота правильной треугольной пирамиды равна 12см, сторона основания 15см. Найти площадь полной поверхности пирамиды.

Практическая работа№ 4

Сечения в призме и пирамиде

Теоретический опрос.

1.Что такое многогранник?

Многогранник-это тело, граница которого состоит из многоугольников

2. Какой многогранник называют выпуклым?

Многогранник называется выпуклым, если все его диагонали расположены внутри него.

3. Как называется многогранник, две грани которого равные многоугольники с соответственно параллельными сторонами, остальные грани параллельными, плоскости которых параллельны прямой?

Призма.

4. Назовите три метода построения сечений многогранников; которые наиболее эффективны и доступны в практике преподавания геометрии в средней школе.

Метод следов, метод вспомогательных сечений, комбинированный метод.

5. Как называется многогранник, у которого одна — грань- это произвольный многоугольник. А остальные грани треугольники с общей вершиной?

Пирамида.

6. Какой параллелепипед называется прямоугольным?

Когда у него все шесть граней прямоугольники.

7. Каким соотношением связаны диагональ прямоугольного параллелепипеда и его рёбра?

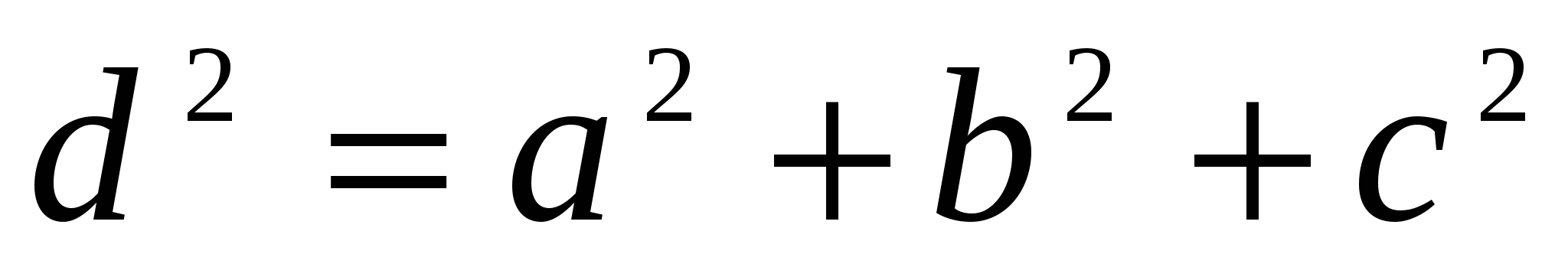
Система устных упражнений по теме:

Цели:

1. Проверить степень усвоения пройденного материала;

2. Развить культуру речи;

3. Совершенствовать навыки решения задач по данной теме.

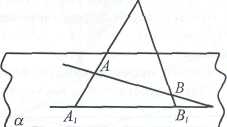
Пример №1. Построить точку пересечения заданной прямой АВ с основной плоскостью.

Решение:

Пусть A₁, В₁ - основания точек А и В. В случае внутреннего параллельного проектиро­вания AA₁\\BB₁ в случае центрального АА₁ и ВВ₁ пересекаются в центре проектирования S. A₁ В₁ принадлежат плоскости а. Точка X - пе­ресечение АВ и А₁В_] будет точкой пересечения прямой АВ с плоскостью а. Если АВ\\А₁В₁ , то АВ\\а

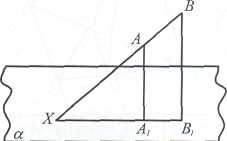
а) Параллельное проектирование S б) Центральное проектирование

Пример №2. Плоскость задана тремя точка­ми Р, Q, R. Построить линию пересечения ее с основной плоскостью, то есть след плоскости PQR.

Решение:

Задача сводится к предыдущей. Находит­ся точка пересечения прямой PQ с плоскостью а — точка X; точка пересечения прямой PR с плоскостью а - точка Y; тогда XY — след плос­кости Р.

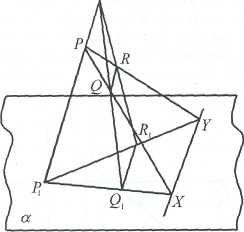
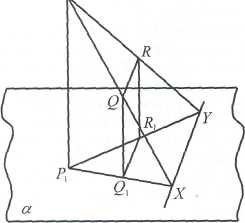
а) параллельное проектирование S б) центральное проектирование

Самостоятельная работа.

Цели:

1. Проверить степень усвоения пройденного материала;

2. Развить логическое мышление;

3. Совершенствовать навыки решения задач по данной теме.

1 вариант

Построить сечение куба DKEFD₁K₁E₁F₁ плоско­стью, проходящей через точки А, В, и С, данные на ребрах K₁E₁, KE и D₁K₁.

2 вариант

Построить сечение четырех­угольной пирамиды SABCD плоскостью, проходящей через три точки К, L, М,данные на ребрах SA, SB, SCпирамиды.

Контрольная работа

1 вариант

1. Построить сечение шестиугольной призмы плоскостью, заданной точками M, N и P на боковых гранях.

2. Построить сечение пятиугольной пирамиды, если плоскость проходит через т. M, принадлежащую боковому ребру, т. N, принадлежащую одной из граней пирамиды и т. P, лежащую на продолжении бокового ребра.

2 вариант

1. Построить сечение шестиугольной пирамиды плоскостью, заданной точками M, N и P на боковых не соседних гранях.

2. Построить сечение параллелепипеда, если плоскость проходит через т.M и N на боковых рёбрах и т. P на плоскости боковой грани, но не принадлежащей этой грани.

3 вариант

1. Построить сечение пятиугольной призмы плоскостью, заданной точкамиM, N и P на боковых не соседних рёбрах.

2. Построить сечение шестиугольной пирамиды, если плоскость проходит через т. M и N на двух различных боковых гранях и т. P на продолжении бокового ребра.

Практическая работа № 5

Тема: Цилиндр

Цели:

– научиться строить чертежи к задачам;

– научиться находить основные элементы конуса и цилиндра;

– научиться находить площади боковой и полной поверхностей конуса и цилиндра.

Оснащение занятия: учебник, конспект, плакаты, модели.

Порядок выполнения работы

Задание 1. Повторите учебный материал.

Вопросы для повторения:

1. Что называется, цилиндром?

2. Дайте определение радиусу, высоте, образующей цилиндра.

3. Какая фигура является осевым сечением цилиндра?

4. Когда сечением цилиндра является круг?

5. Чему равны боковая и полная поверхности цилиндра?

Задание 2. Организуйте работу парами и задайте друг другу вопросы, которые начинаются со слов «Что», «Какая», «Чему».

Задание 3. Выполните № 523, № 525, № 527, № 547, № 553, № 568.

Контроль знаний студентов

– проверить практическую работу;

– решить задачи.

1. Площадь осевого сечения цилиндра 108 кв. см., диаметр основания 6см. Найти площадь боковой поверхности цилиндра.

2.Радиус основания цилиндра равен 2м, высота 3м. Найти диагональ осевого сечения.

3.Осевое сечение цилиндра – квадрат, площадь которого 25. Найти площадь основания.

4.Диагональ осевого сечения цилиндра, равная 4√2, образует с плоскостью основания угол 45^о. Найти боковую поверхность цилиндра.

5.Площадь осевого сечения цилиндра равна 6/ π. Найти площадь его боковой поверхности.

Литература: Атанасян Л. С. Геометрия стр. 125, стр.130.

Практическая работа № 6

Тема: Конус, шар и сфера

Цели:

– научиться строить чертежи к задачам;

– научиться находить основные элементы конуса и цилиндра;

– научиться находить площади боковой и полной поверхностей конуса и цилиндра.

Оснащение занятия: учебник, конспект, плакаты, модели.

Порядок выполнения работы

Задание 1. Повторите учебный материал.

Вопросы для повторения:

1. Что такое конус, вершина конуса, образующая и высота конуса?

2. Что такое осевое сечение конуса?

3. Чему равны боковая и полная поверхности конуса?

4. Дайте определение усеченного конуса.

5. Чему равны боковая и полная поверхности усеченного конуса?

Задание 2. Организуйте работу парами и задайте друг другу вопросы, которые начинаются со слов «Что», «Какая», «Чему».

Задание 3. Выполните № 523, № 525, № 527, № 547, № 553, № 568.

Контроль знаний студентов:

– проверить практическую работу;

– решить задачи.

1. Площадь осевого сечения конуса 32 кв. см, высота равна 4см. Найти площадь полной поверхности конуса.

2. Площадь основания конуса 36π см², а его образующая 10 см.
Вычислить боковую поверхность конуса.

3. Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.

4. Высота конуса равна 6, образующая равна 10. Найдите площадь боковой поверхности конуса.

5. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 1,5 раза?

6. Составьте уравнение сферы с центром в точке А(2;0;-3) и радиусом 4.

Литература: Атанасян Л. С. Геометрия стр. 125, стр.130.

Практическая работа № 7

Практическая работа № 8

Практическая работа № 9

Содержание работы

Вариант 1

1.Найти НОД и НОК чисел:

а) 154 и 210б) 255 и 510

2. Найдите остаток отделения на 3 числа:

а) 1 234 321; б) 55 555;в)155 555

3. Записать в виде десятичной дроби

а) 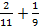; б)

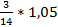
4. Сравните числовые значения выражений: ;

5. Вычислить: а)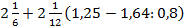

б) 400 · 8 – 2000 : 20 + 450

в) (3212 : 44 + 14) · 61

6. Вычислить: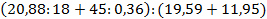

Вариант 2

1.Найти НОД и НОК чисел:

а) 120 и 144б) 105 и 165

2. Найдите остаток отделения на 9 числа:

а) 1 234 567; б) 55 555;в)155 555

3. Записать в виде десятичной дроби

а) 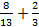; б)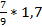

4. Сравните числовые значения выражений: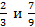

5. Вычислить: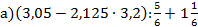

б) (8007 + 32415) : 3 · 10

в) 64 · 10 – (26000 : 100) + 234

6. Вычислить: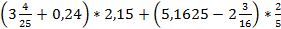

Вариант 3

1.Найти НОД и НОК чисел:

а) 75 и 60 б) 48 и 36

2. Найдите остаток отделения на 3 числа:

а) 1 234 321; б) 55 555; в)155 555

3. Записать в виде десятичной дроби

а) 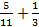; б)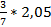

4. Сравните числовые значения выражений: ;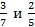

5. Вычислить: а)

б) 400 · 8 – 2000 : 20 + 450

в) (3212 : 44 + 14) · 61

6. Вычислить: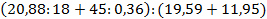

Вариант 4

1.Найти НОД и НОК чисел:

а) 72 и 128 б) 15 и 33

2. Найдите остаток отделения на 9 числа:

а) 1 234 567; б) 55 555; в)155 555

3. Записать в виде десятичной дроби

а) 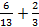; б)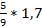

4. Сравните числовые значения выражений: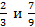

5. Вычислить: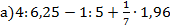

б) (8007 + 32415) : 3 · 10

в) 64 · 10 – (26000 : 100) + 234

6. Вычислить: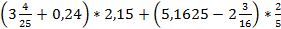

Практическая работа № 10

Подготовительный этап.

Повторение опорных знаний.

1) Проверка усвоения пройденного материала фронтально (или индивидуально) по следующим вопросам (на экран проектируются вопросы, на которые студенты отвечают устно).

1. Какие уравнения называются рациональными?

2. Какие способы решения рациональных уравнений вам известны?

Теоретический этап.

Применение знаний при решении типовых заданий.

1. Решите уравнение:

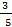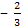а) а+7= а–3

б) (6х–1)(4–х)=0

в)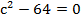

2. Решите неравенство:

а) (5–3х) (0,2х–10) ≥ 0

б) 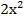–7х–4<0

Практический этап.

Самостоятельное применение умений и знаний.

Провести самостоятельную работу в 5 вариантах.

Варианты для самостоятельной работы.

Вариант 1

1.Решить уравнение:

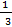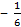а. у+2= у+5

б. (х+2)(х-1)=0

в.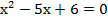

г. 7х–1=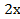

д. (х–5)(2х+8)=0

е.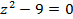

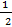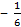ж. у–3= у–7

з. –3х(0,6х–12)=0

и.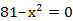

Вариант 2

1.Решить уравнение:

а. 2х–(5х–6)=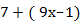

б. (5–2х)(7+3х)=0

в.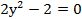

г. 3х–1= 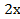– (4–х)

д. (у–3)(у+4) (3у–5) =0

е.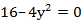

ж. 2(х–3)=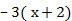

з. 5х(х+1)(3х–17)=0

и.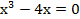

Вариант 3

1.Решить уравнение:

а. 2(х–5) –7(х+2)=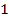

б. 6х(4х–6)(7–х)=0

в.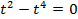

г. 5х–(2х–9)=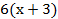

д. 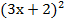=0

е.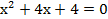

ж. 7х–8= 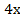– (1–3х)

з. (х–3)(х+6) =0

и.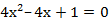

Вариант 4

1.Решить уравнение:

а. 2(х+4) =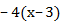

б. 8у(2–у)(у+1)=0

в. ( –1)( – )=0

г. 2(х–14) =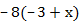

д. 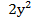+5у=0

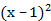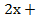е. ( 1)=0

ж. 3(х+4) =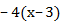

з. 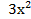–4х=0

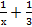и. ( +1) ( )=0

Вариант 5

1.Решить уравнение:

а. –6(2х–5) =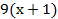

б. 3х - 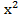=0

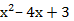в. = 0

г. 0,6(х–9) =02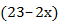

д. (5х–2) (2–3х)=0

е. 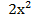–7х+3=0

ж. –8(2х–3) =12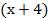

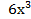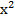з. –3 =0

и. 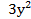–11у–20=0

Список литературы.

1.Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 клас­сы. — М., 2014.

Практическая работа № 11

План занятия

Подготовительный этап.

Повторение опорных знаний.

1) Проверка усвоения пройденного материала фронтально (или индивидуально) по следующим вопросам (на экран проектируются вопросы, на которые студенты отвечают устно).

1. Какие неравенства называются рациональными?

2. Какие способы решения рациональных неравенств вам известны?

Теоретический этап.

Применение знаний при решении типовых заданий.

1. Решите уравнение:

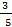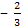а) а+7= а–3

б) (6х–1)(4–х)=0

в)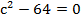

2. Решите неравенство:

а) (5–3х) (0,2х–10) ≥ 0

б) 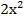–7х–4<0

Практический этап.

Самостоятельное применение умений и знаний.

Провести самостоятельную работу в 15 вариантах.

Список литературы.

1.Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 клас­сы. — М., 2014.

Варианты для самостоятельной работы.

Вариант 1

1. Решить неравенство:

а. х+6 >2-3х

б. 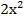-7х+3≤ 0

в. 6х–7 >3+4х

г. 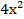+х–3≥0

д. 3х–6 >4–9х

е. 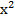–2х+2<0

Вариант 2

1. Решить неравенство:

а. 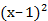–5≤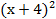

б. 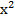–6х+13>0

в. 3х+7 >7х–9

г. 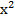+7х–18≤0

д. х–3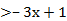

е. 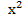+2х–35≤0

Вариант 3

1. Решить неравенство:

а. 6х–7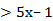

б. 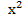–6х+8≤0

в. 3х+6>8х–4

г. 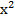(х–3)(х–6)≤0

д. 3х >4х+1

е. 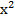–3х+2≤0

Вариант 4

1. Решить неравенство:

а. 4х+3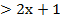

б. 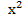+х–6≤0

в. –3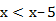

г. 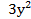–11у+20≥0

д. 5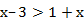

е. 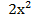–7х+3≤0

Вариант 5

1. Решить неравенство:

а.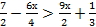

б. 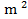–2m–3≤0

в. 4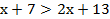

г. 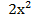–9х+10≤ 0

д. 3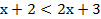

е. 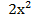+х–15≥0

Практическая работа № 12

Практическая работа № 13

Тема: Преобразование графиков функций.

Цель: Постройте графики функций, используя различные преобразования, ответьте на вопрос задачи.

Методические указания

Работа рассчитана на 10 вариантов, номер варианта совпадает с последней цифрой порядкового номере в списке. Например, 1, 11, 21, 31 …выполняют 1 вариант, 2,12, 22 … - 2 вариант, и т.д.

Работа состоит из двух частей: первая часть задания 1 – 5, это задания которые обязательно нужно выполнить, чтобы получить зачет, если эти задания выполнены с ошибкой, необходимо их исправить и снова сдать работу на проверку. Вторая часть, содержит задания, выполнив которые, вы можете заработать дополнительную оценку: основная часть +2 задания – «4», основная часть +3 задания – «5».

Задание 1. Графиком линейной функции является прямая, для ее построения достаточно двух точек. (значения аргумента х берем произвольно, а значение функции у, считаем подставляя в формулу).

Чтобы проверить проходит ли график функции через указанную точку нужно координаты точки подставить вместо х и у, если получили верное равенство, то прямая проходит через указанную точку, в противном случае – не проходит.

Задание 2, 3, 4. Графики указанных функций получаются из графиков функций 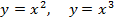, 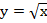используя сдвиг вдоль оси х или у.

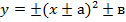, сначала строим график функци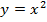и или 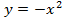, затем сдвигаем его на «а» единиц вправо или влево (+а – влево, - а вправо), затем сдвигаем на «в» единиц вверх или вниз (+в – вверх, -в – вниз)

Аналогично с другими функциями:

Задание 5 Чтобы построить график функции: 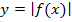, нужно: 1) построить график функции 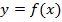, 2) часть графика которая находится выше оси х оставить без изменения, 3) часть графика, которая находится ниже оси х зеркально отобразить.

Задачи для самостоятельного решения.

Обязательная часть

Задание 1. Постройте график линейной функции, определите, проходит ли график функции через указанную точку:

1. 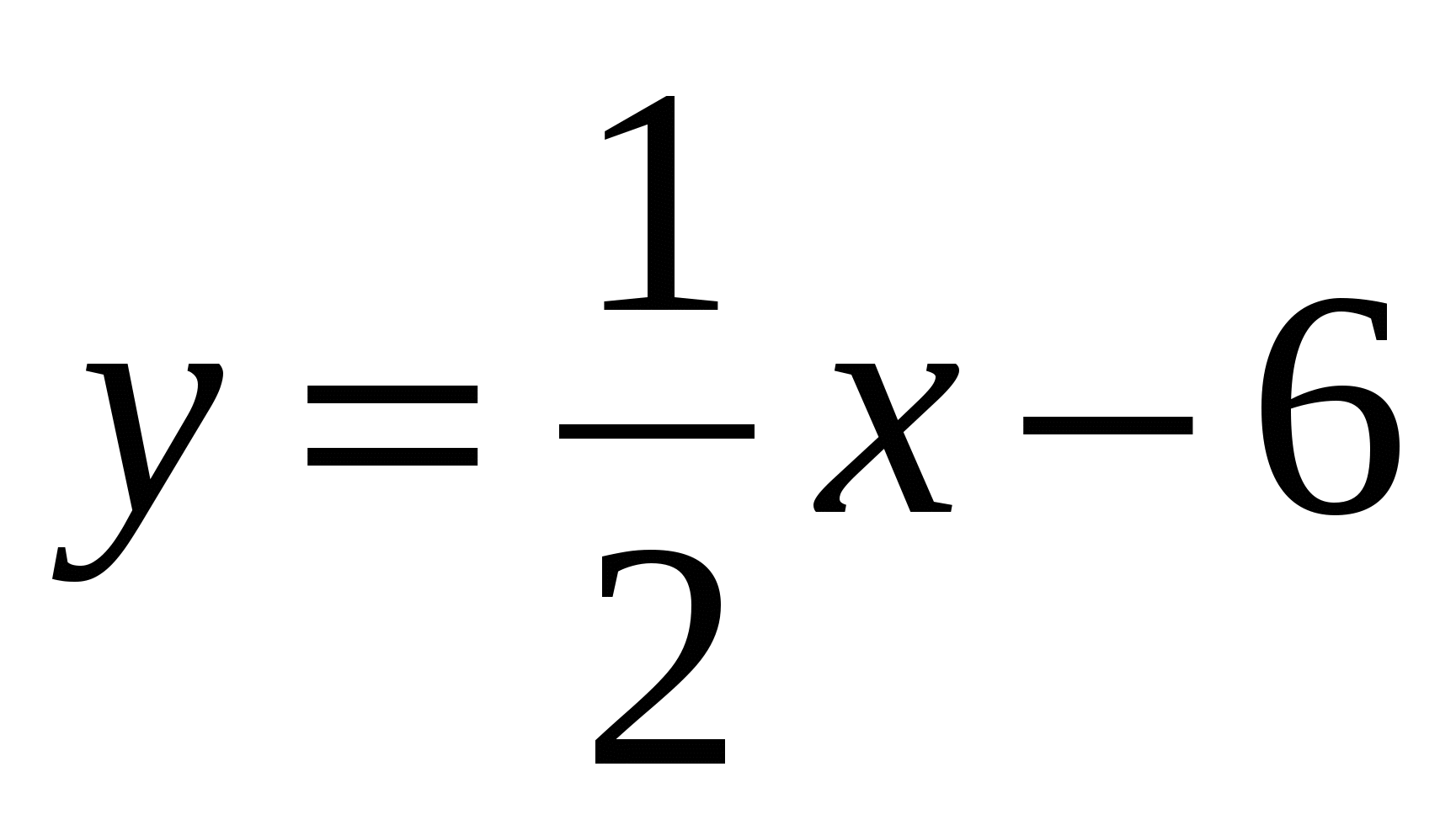, А(42 ;26)

2. 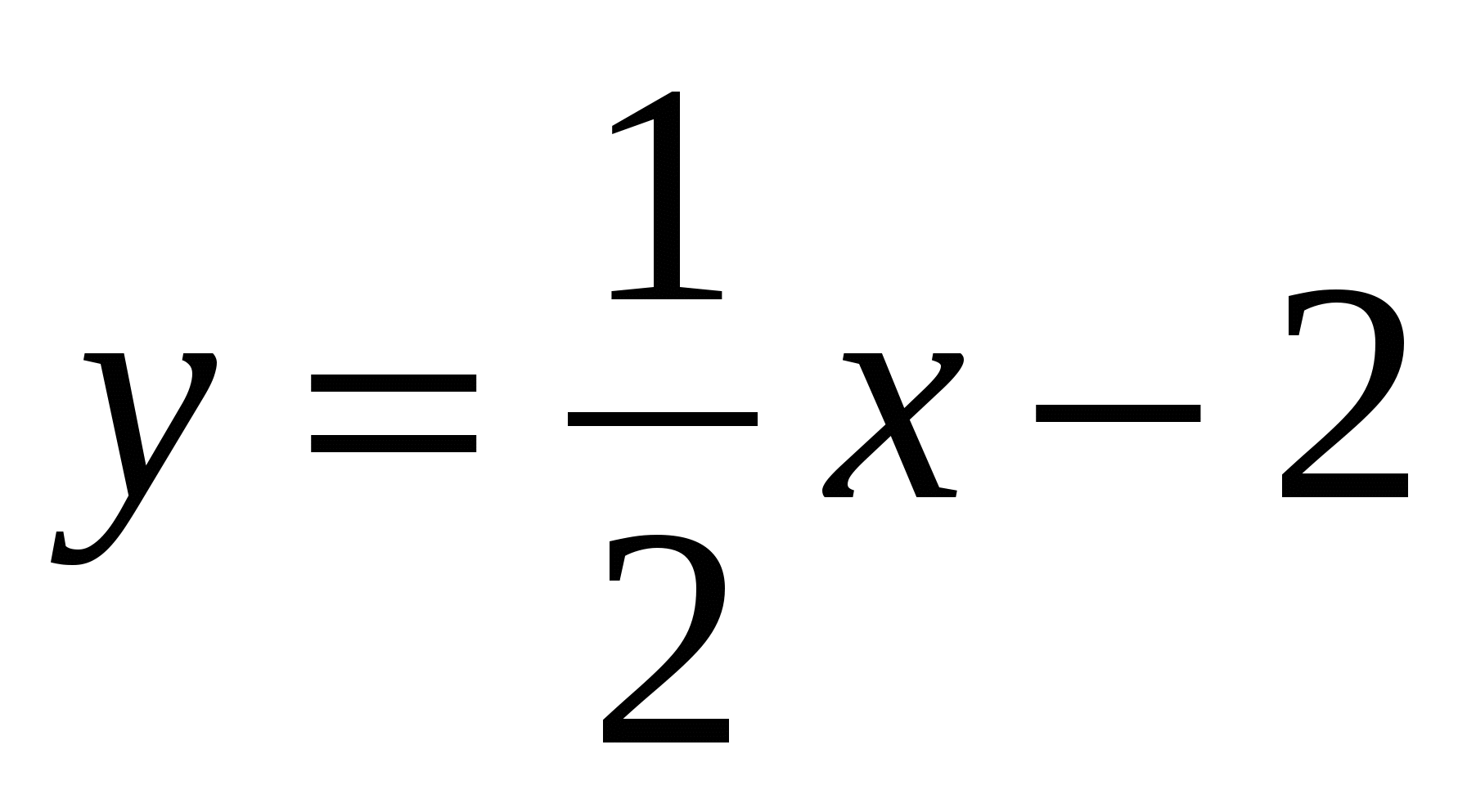, В(42;19)

3. 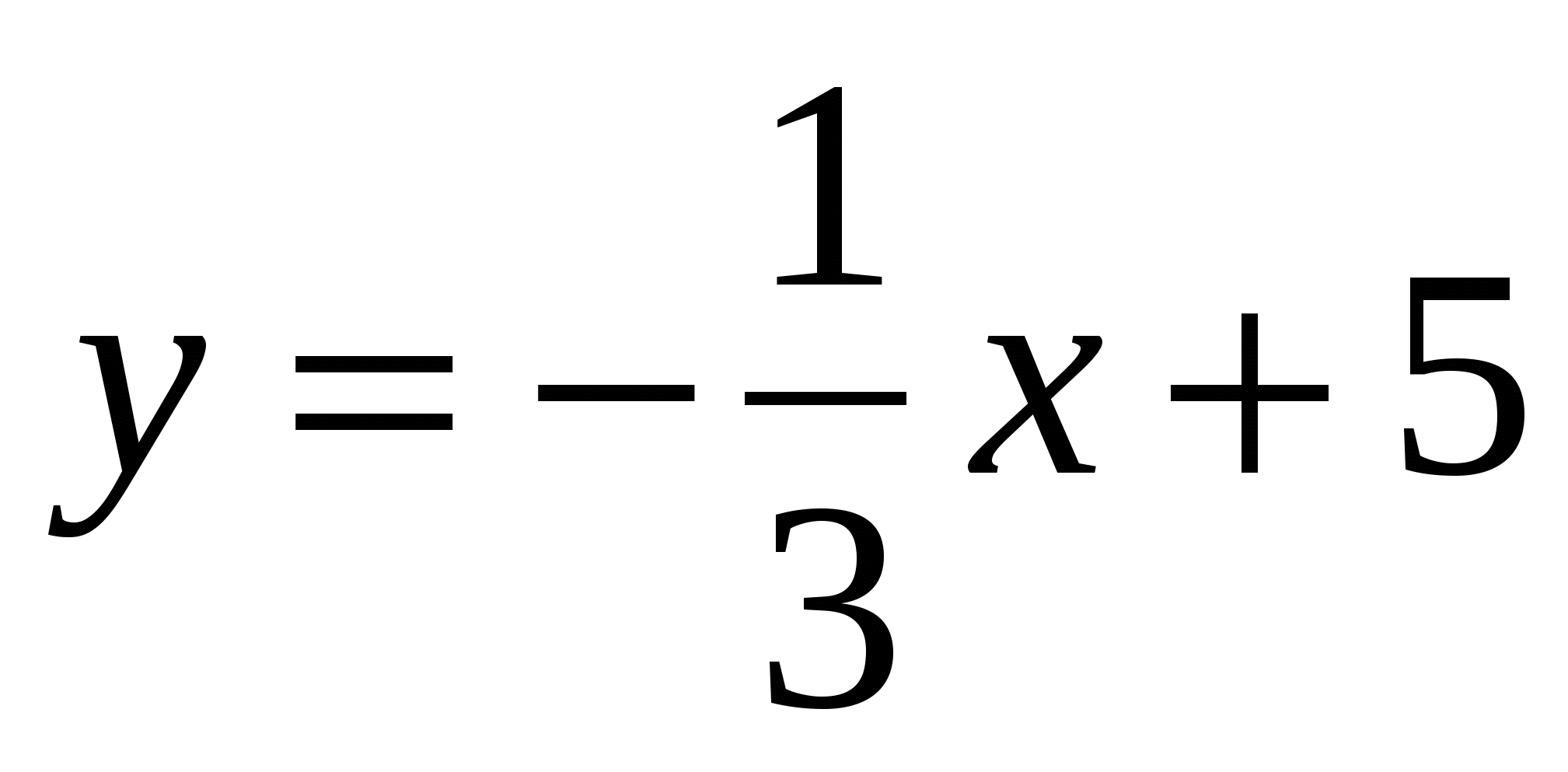. С(-33;6)

4. 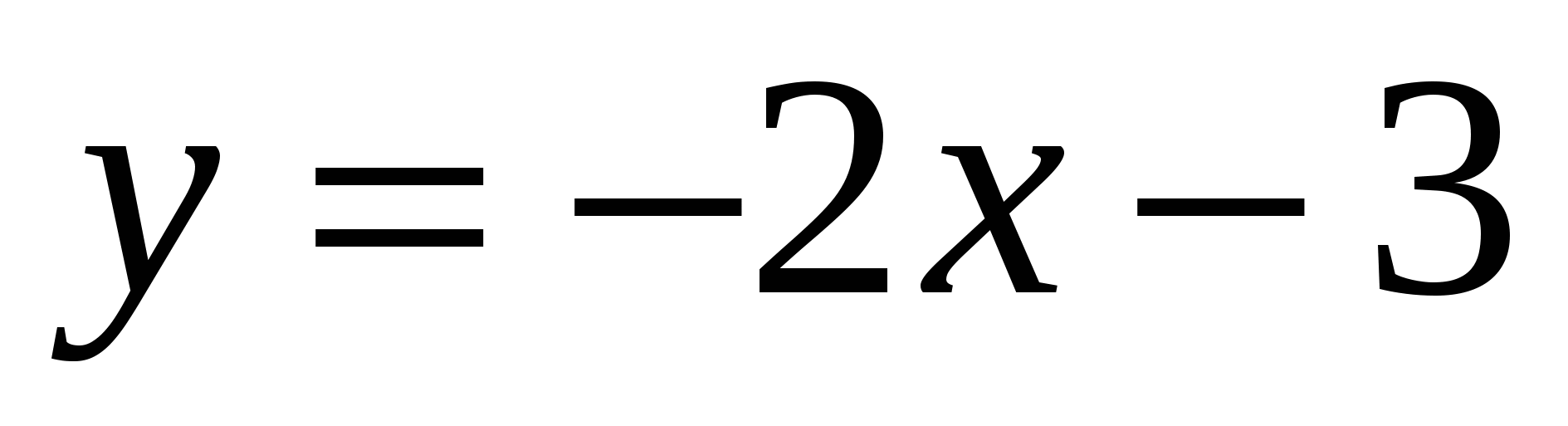D(-40;77)

5. 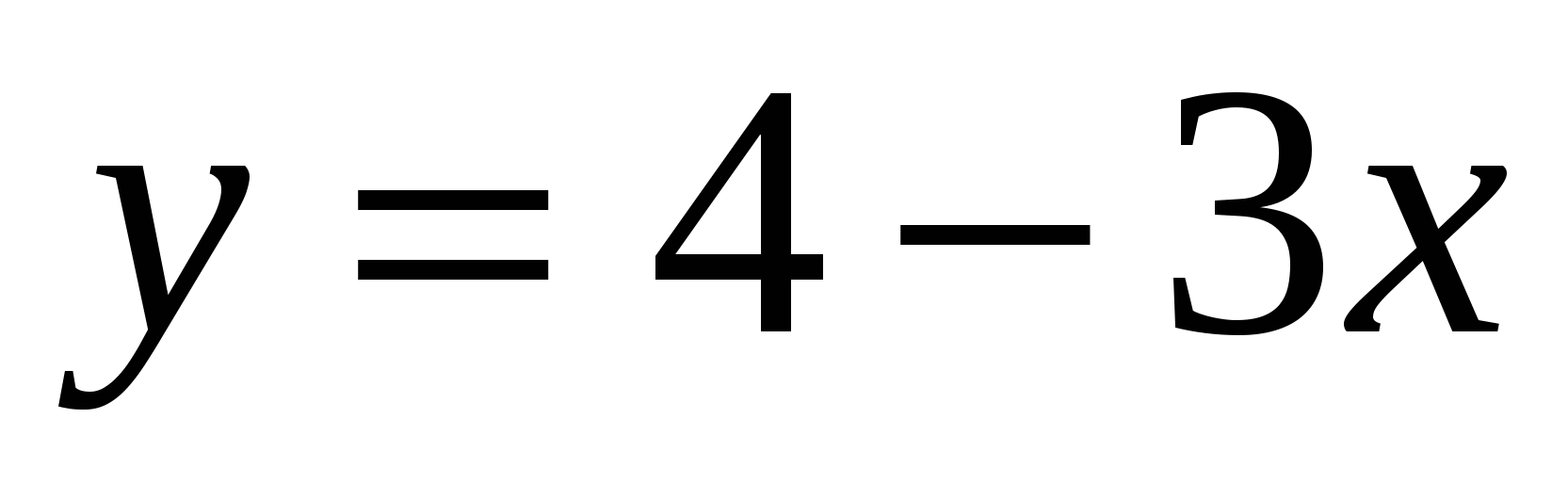, M(20;64)

6. 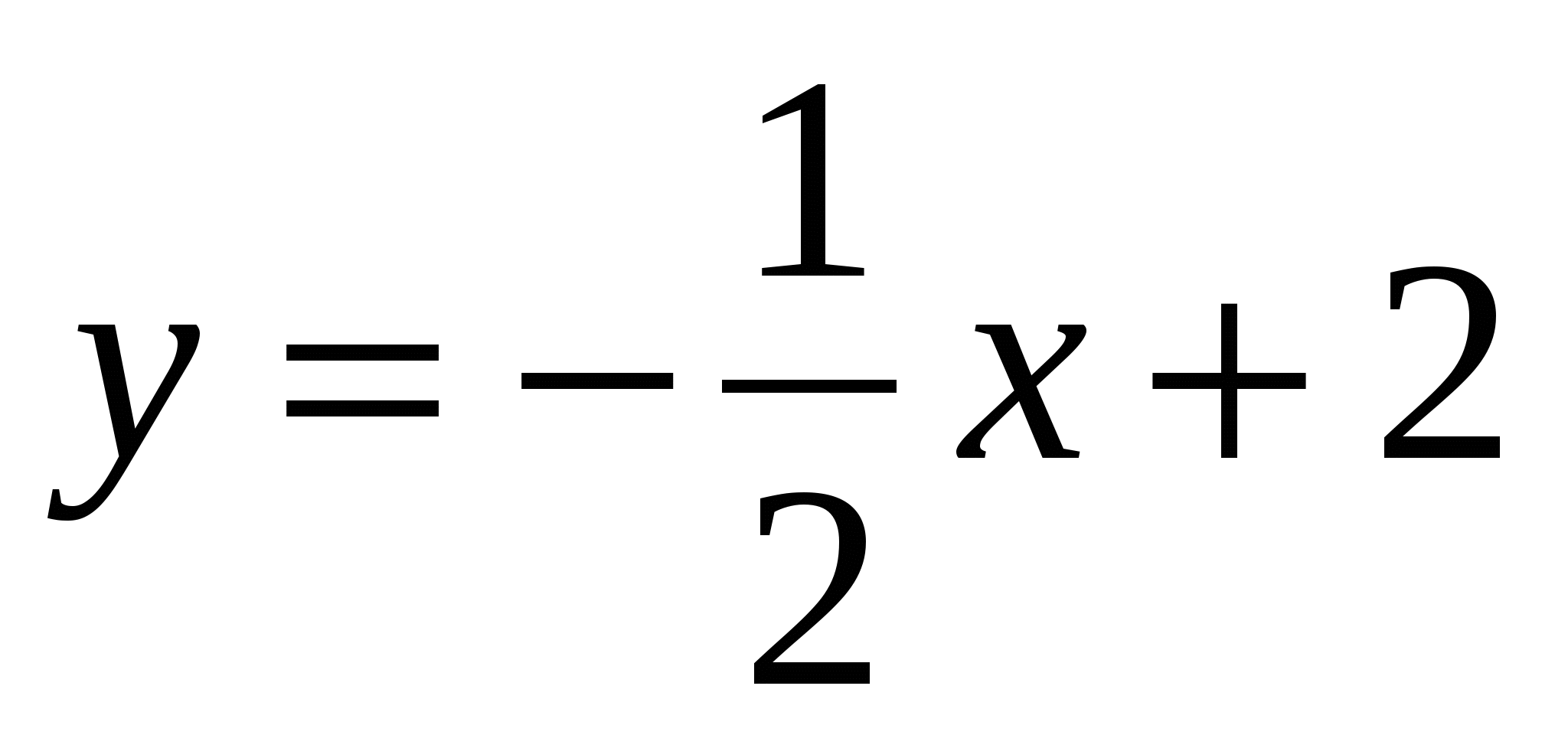E(-20;8)

7. 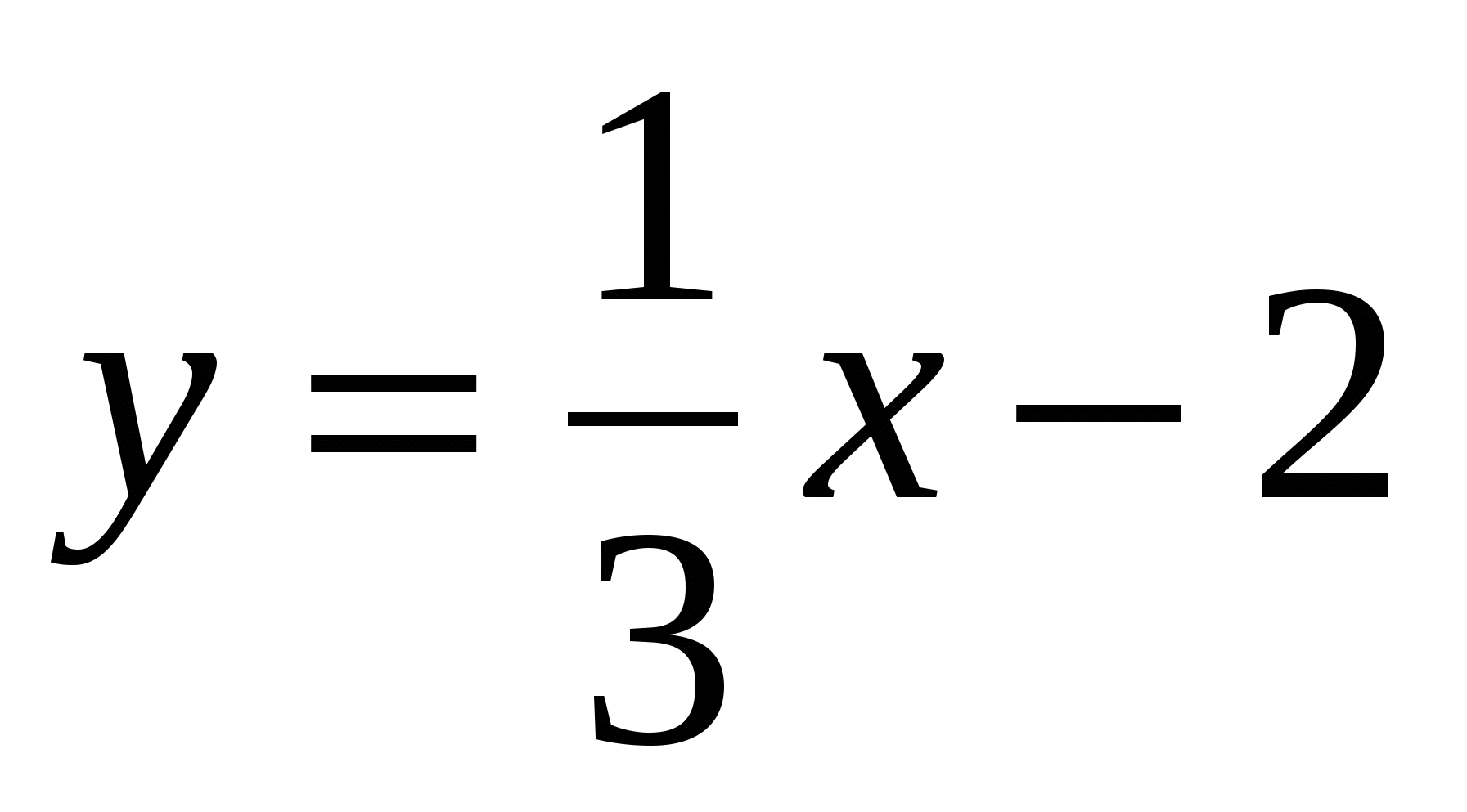,F(60;18)

8. 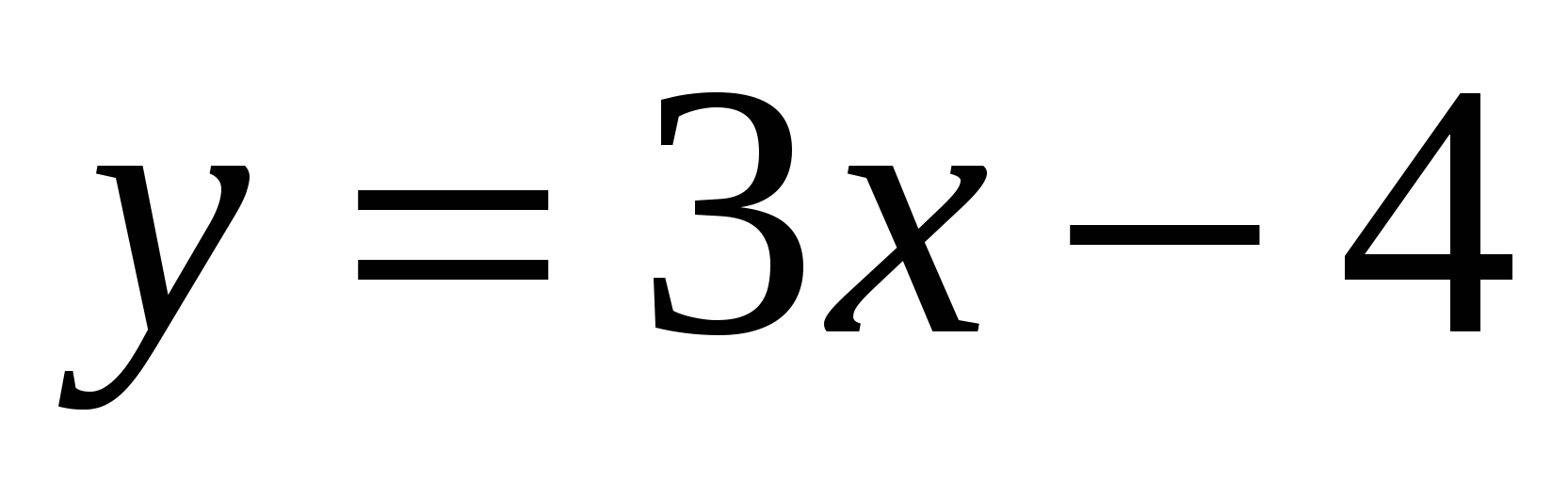, K(-30;86)

9.