Теорема о равномощности конечного множества только одному отрезку натурального ряда

Теорема: конечное множество равномощно только одному отрезку натурального ряда

Доказательство: отрезок не может быть равномощным отрезку , если

ММИ(n)

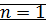
?! Противоречие

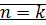
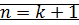
если ?!

если

можем считать, что

Рассмотрим ограничения отображения 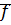на , т.к. 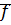- биекция, то ни один из элементов отрезка не отображается в элемент .

инъекция – инъекция

– биекция . ⊠

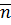Определение: Пусть , число называется количеством элементов множества .

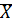Лемма о наибольшем и наименьшем элементе в конечном множестве. Бесконечность множества натуральных чисел

Лемма: Каждое не пустое конечное множество содержит наибольший и наименьший элемент

Доказательство: ММИ по количеству 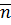элементов в множестве

если в множестве 1элемент, то он и наименьший и наибольший

, ,

каждое конечное множество 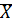, в котором 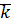элементов, содержит наибольший и наименьший элемент.

, ,

По предположению индукции в множестве выберем наибольший элемент и обозначим его . Сравниваем и и выбираем наибольший элемент. Это и будет наибольший элемент множества 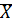.Аналогично находим наименьший элемент множества . ⊠

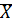Теорема: Множество всех натуральных чисел бесконечно

Доказательство (от противного): По лемме, в каждом конечном множестве существует наибольший элемент , но . Получили противоречие. Следовательно, максимального элемента нет, а значит множество натуральных чисел бесконечно. ⊠

Счетность множеств целых и рациональных чисел. Несчетность множества действительных чисел

32. Отношение эквивалентности на множестве N². Определение целого числа как класса эквивалентности на N². Примеры

Определение: Пусть . 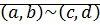если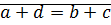

Пример:

…

Теорема: Отношение (эквивалентности) является отношением эквивалентности.

Доказательство:

рефлексивность:

симметричность: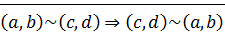

транзитивность: ?

⊠

Свойство:

Доказательство: ⊠

Определение:Целым числом будем называть класс эквивалентности относительно отношения эквивалентности на .

Мн-во всех классов эквивалентности наз. множеством целых чисел и обозначается .

класс эквивалентности пары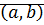

фактор-множество по отношению эквивалентности.

Пример:

, ,

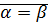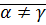Определение суммы целых чисел и его корректность

Определение: суммой целых чисел называется целое число .

Теорема (корректность определения суммы): сумма не зависит от выбора представителя класса (суммы эквивалентных пар – эквивалентны).

Доказательство: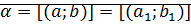

Докажем: ?

Свойство сложения целых чисел. Аддитивная абелева группа целых чисел

Теорема (коммутативность сложения):

Доказательство: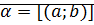

⊠

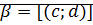
Теорема (ассоциативность сложения):

Доказательство: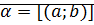

⊠

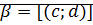
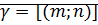
Свойство: целое число явл. нейтральным отн. сложения в Z

.

Доказательство:

⊠

Определение: целое число наз. нулем.

Свойство: , который явл. противоположным к эл-ту 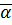относительно сложения.

Доказательство: ?

⊠

Следствие: аддитивная абелева группа.