Динамическое программирование

Задание 1.

По данным таблицы построить схему дорожной сети и найти методом динамического программирования оптимальный маршрут.

Задание 2.

Определить методом динамического программирования оптимальную политику замены оборудования.

Задание 3.

Методом динамического программирования найти оптимальное распределение ресурсов.

Задания для контрольной работы.

#1.

3.1.

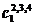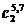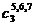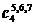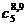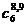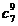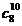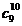6,2,6	7,3	9,2,8	5,2,9	4,6	7,4

#2.

3.1.

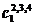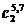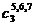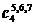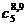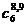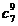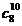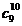3,5,4	1,6	2,7,4	6,8,3	7,2	9,2

#3.

3.1.

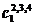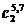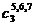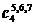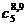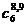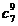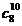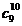7,3,5	2,7	9,3,1	8,4,5	2,6	1,9

#4.

3.1.

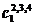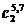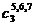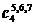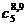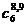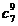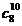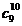1,6,2	5,3	6,8,4	7,2,9	5,3	6,1

#5.

3.1.

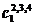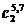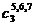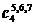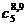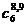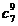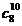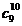4,6,1	3,5	7,3,6	2,5,9	1,8	2,3

#6.

3.1.

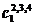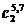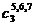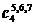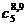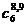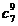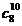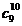1,9,3	8,7	4,9,3	7,4,8	6,3	1,8

#7.

3.1.

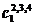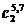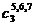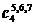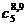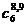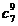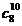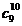4,8,4	6,1	9,3,5	4,8,2	7,4	9,6

#8.

3.1.

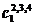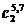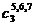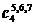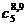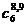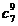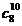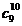5,3,8	2,5	8,1,7	5,9,1	3,5	8,4

#9.

3.1.

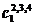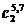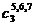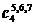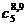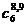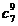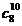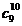8,1,5	9,2	6,8,4	5,2,6	1,8	3,6

#10.

3.1.

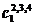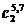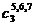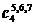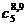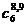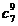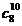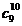9,2,5	3,7	4,6,8	1,3,5	8,7	1,4

#12.

3.1.

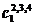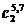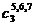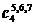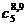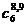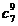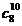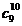4,4,6	1,5	2,9,9	4,5,5	1,8	9,4

#13.

3.1.

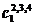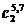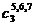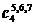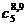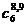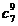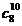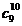8,5,3	4,7	2,1,1	5,83	4,9	8,5

#14.

3.1.

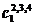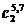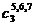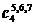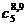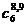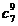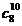4,9,5	6,8	3,7,4	8,3,5	7,7	4,1

#15.

3.2.

t
r (t)
v (t)

N	s	p

#16.

3.2.

t
r (t)
v (t)

N	s	p

#17.

3.2.

t
r (t)
v (t)

N	s	p

#18.

3.2.

t
r (t)
v (t)

N	s	p

#19.

3.2.

t
r (t)
v (t)

N	s	p

#20.

3.2.

t
r (t)
v (t)

N	s	p

#21.

3.2.

t
r (t)
v (t)

N	s	p

#22.

3.2.

t
r (t)
v (t)

N	s	p

#23.

3.2.

t
r (t)
v (t)

N	s	p

#24.

3.2.

t
r (t)
v (t)

N	s	p

#25.

3.2.

t
r (t)
v (t)

N	s	p

#26.

3.2.

t
r (t)
v (t)

N	s	p

#27.

3.2.

t
r (t)
v (t)

N	s	p

#28.

3.2.

t
r (t)
v (t)

N	s	p

#29.

3.2.

t
r (t)
v (t)

N	s	p

#30.

3.2.

t
r (t)
v (t)

N	s	p

#31.

3.2.

t
r (t)
v (t)

N	s	p

#32.

3.2.

t
r (t)
v (t)

N	s	p

#33.

3.2.

t
r (t)
v (t)

N	s	p

#34.

3.2.

t
r (t)
v (t)

N	s	p

#35.

3.3.

	Прирост объема продаж в зависимости от выделяемых инвестиционных ресурсов, ден.ед.
Номер подразделения

#36.

3.3.

	Прирост объема продаж в зависимости от выделяемых инвестиционных ресурсов, ден.ед.
Номер подразделения

#37.

3.3.

	Прирост объема продаж в зависимости от выделяемых инвестиционных ресурсов, ден.ед.
Номер подразделения

#38.

3.3.

	Прирост объема продаж в зависимости от выделяемых инвестиционных ресурсов, ден.ед.
Номер подразделения

#39.

3.3.

	Прирост объема продаж в зависимости от выделяемых инвестиционных ресурсов, ден.ед.
Номер подразделения

#40.

3.3.

	Прирост объема продаж в зависимости от выделяемых инвестиционных ресурсов, ден.ед.
Номер подразделения

#41.

3.3.

	Прирост объема продаж в зависимости от выделяемых инвестиционных ресурсов, ден.ед.
Номер подразделения

#42.

3.3.

	Прирост объема продаж в зависимости от выделяемых инвестиционных ресурсов, ден.ед.
Номер подразделения

#43.

3.3.

	Прирост объема продаж в зависимости от выделяемых инвестиционных ресурсов, ден.ед.
Номер подразделения

#44.

3.3.

	Прирост объема продаж в зависимости от выделяемых инвестиционных ресурсов, ден.ед.
Номер подразделения

#45.

3.3.

	Прирост объема продаж в зависимости от выделяемых инвестиционных ресурсов, ден.ед.
Номер подразделения

Теория игр

Задание 1.

После нескольких лет эксплуатации оборудование может оказаться в одном из трех состояний:

1) требуется профилактический ремонт;

2) требуется замена отдельных деталей и узлов;

3) требуется капитальный ремонт.

В зависимости от ситуации руководство предприятия может принять следующие решения:

1) отремонтировать оборудование своими силами, что потребует затрат а;

2) вызвать специальную бригаду ремонтников, расходы в этом случае составят b;

3) заменить оборудование новым, реализовав устаревшее по остаточной стоимости.. Совокупные затраты на это мероприятие составят с.

Требуется найти оптимально решение данной проблемы по критерию минимизации затрат с учетом следующих предположений:

а) на основе обобщения опыта эксплуатации аналогичного оборудования определены вероятности наступления соответствующих состояний – q;

б) имеющийся опыт свидетельствует о равной вероятности наступления соответствующих состояний;

в) о вероятностях наступления соответствующих состояний ничего определенного сказать нельзя.

Задание 2.

Предприятие планирует выпуск трех видов продукции. Не проданная в сезон продукция реализуется с уценкой. В приводимых таблицах d – себестоимость ед. продукции; p – цена в сезон; r – цена после окончания сезона; a,b,c – объемы спроса (в тыс. ед.) при повышенном, среднем и низком уровне спроса в сезон. Составить оптимальный план выпуска.

Примечание: составлять матрицы по продуктам

Задание 3.

За некоторый период времени потребление сырья в зависимости от его качества составляет b единиц. Если для выпуска запланированного объема продукции сырья окажется недостаточно, то его запас можно пополнить, что потребует дополнительных затрат c₁ в расчете на ед. сырья. Если же запас превысит потребности, то дополнительные затраты на хранение остатка составят c₂ в расчете на ед. сырья. Необходимо дать рекомендации об оптимальном объеме запаса сырья с учетом следующих предположений:

а) вероятности потребностей в сырье q известны;

б) потребление сырья в указанных количествах равновероятно;

в) о вероятностях потребления ничего определенного сказать нельзя.

Задание 4.

Задания данного подраздела сформулированы для вариантов 31-35 в виде отдельных задач.

Вариант
#1		4.2	d	p	r	a	b	c
			1,3	2,6	2,1
			1,7		1,8
			0,9	1,8	0,7
#2		4.1		П1	П2	П3
			a
			b
			c
			q	0,3	0,5	0,2
			(λ =	0,7)
#3		4.1		П1	П2	П3
			a
			b
			c
			q	0,4	0,45	0,15
			(λ =	0,9)
#4		4.1		П1	П2	П3
			a
			b
			c
			q	0,15	0,6	0,25
			(λ =	0,5)
#5		4.1		П1	П2	П3
			a
			b
			c
			q	0,15	0,55	0,3
			(λ =	0,8)
#6		4.1		П1	П2	П3
			a
			b
			c
			q	0,2	0,65	0,15
			(λ =	0,6)
#7		4.2	d	p	r	a	b	c
			1,8	2,7	1,4
			2,5	3,8	2,6
			0,9	3,8	0,8
#8		4.2	d	p	r	a	b	c
			3,2	4,7	3,5
			1,8	2,5	1,2
			2,7	3,8	2,1
#9		4.2	d	p	r	a	b	c
			2,6	3,4	2,8
			3,7	4,2	3,2
			1,5	2,8	1,7
#10		4.2	d	p	r	a	b	c
			3,8	4,7	3,5
			2,6	3,9	2,8
			3,2	4,5	3,2
#11		4.2	d	p	r	a	b	c
			4,4	5,2	4,1
			2,1	3,5	2,6
			3,5	4,7	3,2
#12		4.3
			b
			q	0,25	0,3	0,25	0,2
			c	c1 = 5	c2 = 7
			λ	0,6
#13		4.2	d	p	r	a	b	c
			1,5	2,3	1,8
			2,1	3,4	2,2
			1,4	2,8	1,6
						Наши рекомендации Занятие № 2 Динамическое программирование Динамическое программирование Динамическое программирование. Динамическое программирование Динамическое программирование Динамическое программирование Динамическое программирование Тема. динамическое программирование Динамическое программирование Динамическое программирование ← Предыдущая страница | Следующая страница →