Дифференциал функции двух переменных первого и высших порядков.

Определение. Дифференциалом функции называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е. .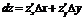

Пример. Найти полный дифференциал функции .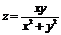

Так как 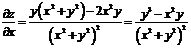, , 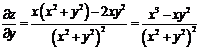то .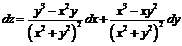

ВОПРОС 50.Производные и дифференциалы высших порядков. Приложения дифференциального исчисления функций нескольких переменных в моделировании социально экономических процессов.

Предположим, что функция f'(x) является дифференцируемой в некоторой точке x интервала (a,b), то есть имеет в этой точке производную. Тогда данную производную называют второй произвоьдной и обозначают f(2)(x), f''(x) или y(2), y''(x). Аналогично можно ввести понятие второй , третьей и т. д. производных. По индукции можно ввести понятие n- ой производной:

y(n) = (y(n-1))'. (6)

Функцию, имеющую на некотором множестве конечную производную порядка n, называют n раз дифференцируемой на этом множестве. Методика нахождения производных высших порядков предполагает умение находить производные первого порядка, о чем говорит формула ( 6).

Если u(x), v(x) две дифференцируемые функции, то для нахождения производной их произведения справедлива формула Лейбница

(u(x)v(x))(n) = u(n)v+nu(n-1)v'+(n(n-1)/2)u(n-2)v''+...+ uv(n) =

= Sk = 0nCnku(n-k)v(k),

где

Cnk = (n(n-1)(n-2)...(n-k+1))/k!, u(0) = u, v(0) = v.

Данная формула Лейбница особенно эффективна в случае, когда одна из перемножаемых функций имеет конечное число отличных от нуля производных и легко вычислить производные другой функции.

Пример 9. Пусть y = ex(x2-1). Найти y(10). Положим u(x) = ex,

v(x) = (x2-1). Согласно формуле Лейбница

y(10) = (ex)(25)(x2-1)+10(ex)(9)(x2-1)'+(10· 9/2) (ex)(8)(x2-1)'',

так как следующие слагаемые равны нулю. Поэтому

y(10) = ex(x2-1)+10ex2x+(10· 9/2)ex (2) = ex(x2+20x+89)

Рассмотрим выражение для первого дифференциала

dy = f'(x)dx.

Пусть функция, стоящая в правой части, является дифференцируемой функцией в данной точке x. Для этого достаточно, чтобы y = f(x), была дифференцируема два раза в данной точке x, а аргумент либо является независимой переменной, либо представляет собой дважды дифференцируемую функцию.

Определение 6 (дифференциал второго порядка). Значение d(dy) дифференциала от первого дифференциала ( 4) при d x = dx, называется вторым дифференциалом функции y = f(x) и обозначается d2y.

Таким образом,

d2y = d (dy)|d x = dx.

Дифференциал dny можно ввести по индукции.

ВОПРОС 51. Локальные и условные экстремумы функций нескольких переменных.

Локальный экстремум.

Пусть дана функция 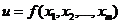, определенная в открытой области 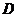пространства 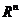, и пусть точка .

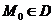Определение1. Точка 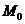называется точкой минимума функции 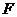если существует окрестность точки, в которой выполняется неравенство:

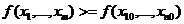, т.е.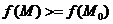

(аналогично точка максимума)

Определение2. Точки минимума и максимума называются точками локального экстремума..

Теорема1.

Необходимое условие экстремума дифференцируемой функции.

Если точка 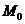является точкой экстремума дифференцируемой функции, то в этой точке все частные производные первого порядка равны нулю.

Определение3. Точка, в которой все частные производные первого порядка

Функции равны нулю, называется стационарной.

Теорема2.

Достаточное условие дифференцируемости

Пусть функция 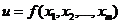в окрестности точки 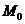имеет непрерывные частные производные второго порядка, и пусть точка 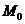является стационарной, тогда необходимо вычислить дифференциал второго порядка:

1) если 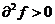и выполняется при любых значениях 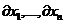, не равных нулю одновременно, то 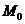- точка минимума.

2) если 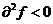и выполняется при любых значениях 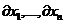, не равных нулю одновременно, то 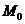- точка максимума.

3) если 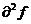принимает значения разных знаков, ТО Экстремума нет.

Условный экстремум.

Определение1. Условный экстремум-это точки условного минимума и максимума.

Метод Лагранжа.

Определение2. функцией Лагранжа называется функция

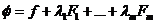
Теорема1.

Если точка 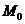является точкой условного экстремума дифференцируемой функции 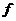, то в этой точке все частные производные первого порядка взятые от функции Лагранжа равны нулю.

Теорема2.

Пусть функция 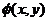в окрестности точки 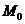имеет непрерывные частные производные второго порядка, и пусть точка 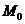удовлетворяет Теореме1 , тогда необходимо вычислить дифференциал второго порядка:

1) если 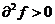и выполняется при любых значениях 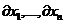, не равных нулю одновременно, то 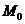- точка минимума.

2) если 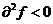и выполняется при любых значениях 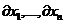, не равных нулю одновременно, то 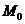- точка максимума.

3) если 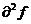принимает значения разных знаков, ТО Экстремума нет.

ВОПРОС 53. Первообразная и неопределённый интеграл. Таблица элементарных интегралов.