Свойства сходящихся последовательностей.

Последовательность, имеющая предел, называется сходящийся, в противном случае – расходящейся.

Рассмотрим свойства сходящихся последовательностей.

1.Сходящаяся последовательность ограничена.

2.Пусть 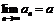, , 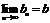тогда , , , .

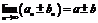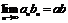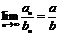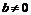3.Если 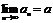, 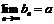и для всех 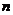выполняются неравенства 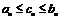, то .

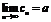4.Если 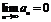и последовательность 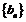- ограниченная, то 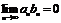(произведение бесконечно малой на ограниченную есть бесконечно малая).

Теорема. Если числовая последовательность 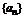монотонна и ограниченна, то она имеет предел.

Теорема. Если в некоторой окрестности точки 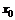(или при достаточно больших значениях 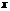) функция 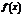заключена между двумя функциям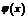и и 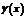, имеющими одинаковый предел 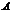при 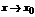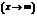, то функция 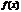имеет тот же предел .

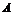28.Определение функции. Способы задания функции.

Определение. Если каждому элементу 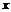множества ставится в соответствие вполне определенный элемент 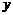множества 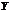, то говорят, что на множестве 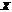задана функция .

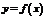Основные свойства функции:

1. Четность и нечетность. Функция 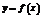называется четной, если для любых значений 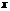из области определения 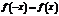и нечетной, если .

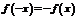2. Монотонность. Функция 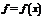называется возрастающей (убывающей) на промежутке 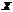, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.

3. Ограниченность. Функция 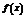называется ограниченной на промежутке 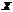, если существует такое положительное числ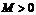о , что 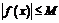для любого .

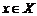4. Периодичность. Функция 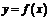называется периодической с периодом 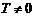, если для любых 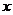из области определения функции .

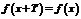Способы задания функций:

1. Аналитический способ, если функция задана формулой вида 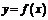. Функция 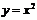задана аналитически.

2. Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента 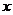и соответствующие значения функции .

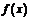3. Графический способ состоит в изображении графика функции – множества точек 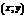плоскости, абсциссы которых есть значения аргумента 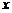, а ординаты – соответствующие им значения функции .

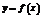Основные элементарные функции:

1. Степенная функция: , , .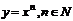

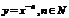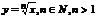2. Показательная функция: .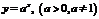

3. Логарифмическая функция: .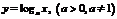

4. Тригонометрические функции , , , .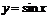

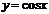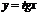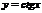5. Обратные тригонометрические функции: , , , .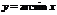

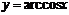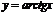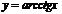Классификация функций:

· Алгебраические (целая рациональная функция, дробно-рациональная функция, иррациональная функция).

· Неалгебраические (трансцендентные).

Преобразование графиков:

График функции 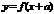есть график функции 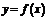, сдвинутый (при 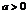влево, при 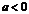вправо) на 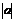единиц параллельно оси .

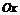1 График функции 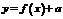есть график функции 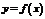, сдвинутый (при 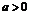вверх, при 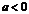вниз) на 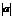единиц параллельно оси .

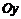2 График функции 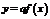, 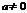есть график функции 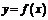, растянутый (при 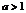) в 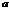раз или сжатый (при 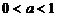) вдоль оси .

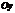3 График функции 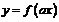, 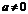есть график функции 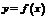, сжатый (при 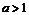) в 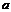раз или растянутый (при 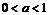) вдоль оси .

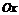4. Словесный способ, если функция описывается правилом ее составления. Например, функция Дирихле: 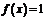, если 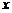- рационально; 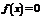, если 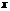- иррационально.

Пример. Построить график функции 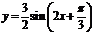преобразованием графика функци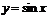и или .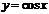

1. Строим график .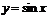

2. График функции 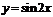есть график функции 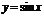, сжатый в 2 раза.

3. График функции 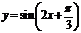есть график функции 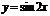, сдвинутый на 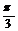влево.

4. График функции 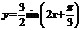есть график функции 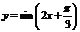, растянутый в 1,5 раза.