Моделирование систем массового обслуживания с использованием метода Монте-Карло.

для оцен­ки качества функционирования систем обслуживания ис­пользуют метод статистических испытаний (метод Монте-Карло). Основой решения задачи исследования функционирования СМО в реальных условиях является статистическое моделирование входя­щего потока требований и процесса их обслуживания. Для решения задачи статистического моделирования функциони­рования СМО должны быть заданы следующие исходные данные: описание СМО; параметры закона распределения периодичности поступлений требований в систему; параметры закона распределения времени пребывания требова­ния в очереди; параметры закона распределения времени обслуживания требо­ваний в системе. Решение задачи статистического моделирования функционирова­ния СМО складывается из следующих этапов. Вырабатывают равномерно распределенное случайное чис­ло ξi. Равномерно распределенные случайные числа преобразуют в величины с заданным законом распределения: интервал времени между поступлениями требований в систему (ΔtTi); время ухода заявки из очереди; длительность времени обслуживания требования каналами (ΔtОi) Определяют моменты наступления событий: поступление требования на обслуживание; уход требования из очереди; окончание обслуживания требования в каналах системы. Моделируют функционирование СМО в целом и накапливают статистические данные о процессе обслуживания. Устанавливают новый момент поступления требования в си­стему, и вычислительная процедура повторяется в соответствии с изложенным. Определяют показатели качества функционирования СМО путем обработки результатов моделирования методами математи­ческой статистики.

38. Транспортные задачи линейного програмирования. Постановка задачи.

Под термином «транспортные задачи» понимается широкий круг задач не только транспортного характера. Общим для них яв­ляется, как правило, распределение ресурсов, находящихся у т производителей, по п потребителям этих ресурсов. На автомобильном транспорте наиболее часто встречаются сле­дующие задачи, относящиеся к транспортным: прикрепление потребителей ресурса к производителям; привязка пунктов отправления к пунктам назначения; взаимная привязка грузопотоков прямого и обратного направле­ний; отдельные задачи оптимальной загрузки промышленного оборудования; оптимальное распределение объемов выпуска промышленной продукции между заводами-изготовителями и др. Транспортная задача называется закрытой, если суммарный объем отправляемых грузов 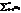равен суммарному объему потребности в этих грузах по пунктам назначения 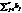. Если такого равенства нет, задачу называют открытой. Для написания модели необходимо все условия и целевую функцию представить в виде математических уравнений. Все грузы из i-х пунктов должны быть отправлены. Все j-е пункты (потребители) должны быть обеспечены грузами в плановом объеме. Суммарные объемы отправления должны равняться суммар­ным объемам назначения. Должно выполняться условие неотрицательности переменных: xij ≥0, , i = 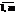, j = 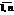. Перевозки необходимо осуществить с ми­нимальными транспортными издержками. Транспортным задачам присущи следующие особенности: распределению подлежат однородные ресурсы; условия задачи описываются только уравнениями; все переменные выражаются в одинаковых единицах измерения; во всех уравнениях коэффициенты при неизвестных равны еди­нице; каждая неизвестная встречается только в двух уравнениях системы ограничений. Транспортные задачи могут решаться симплекс-методом.