Автокорреляцией остатков и ее виды.

Автокорреляция (последовательная корреляция)опреде­ляется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные данные). Автокорреляция остатков (отклоне­ний) обычно встречается в регрессионном анализе при использо­вании данных временных рядов. При использовании перекрестных данных наличие автокорреляции (пространственной корреляции) крайне редко. В силу этого в дальнейших выкладках вместо символа 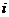порядкового номера наблюдения будем использовать символ t, отражающий момент наблюдения. Объем выборки при этом будем обозначать символом Т вместо 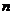. В экономи­ческих задачах значительно чаще встречается так называемая положительная автокорреляция( 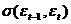> 0), нежели отри­цательная автокорреляция( 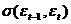< 0).

В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых не учтенных в модели факторов.

Причины возникновения: 1) Ошибки спецификации

2) Инерция

3) Эффект паутины.

4) Сглаживание данных.

Статистика Дарбина–Уотсона. Формула расчета. Суть показателя.

При статистическом анализе уравнения регрессии на началь­ном этапе часто проверяют выполнимость одной предпосылки, а именно: условия статистической независимости отклонений между собой. Поскольку значения 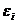теоретического уравнения регрессии

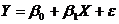остаются неизвестными ввиду неопределенности истинных значений коэффициентов регрессии, то проверяется стати­стическая независимость их оценок – отклонений 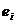, i = 1, 2,..., n. При этом обычно проверяется их некоррелированность, являю­щаяся необходимым, но недостаточным условием независимости. Причем проверяется некоррелированность не любых, а только со­седних величин 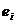. Соседними обычно считаются соседние во вре­мени (при рассмотрении временных рядов) или по возрастанию объясняющей переменной X (в случае перекрестной выборки) значения 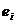. Для этих величин несложно рассчитать коэффициент корреляции, называемый в этом случае коэффициентом автокор­реляции первого порядка.

На практике для анализа коррелированности отклонений вместо коэффициента корреляции используют тесно с ним свя­занную статистику Дарбина—Уотсона DW, рассчитываемую по формуле Суть его состоит в том, что на осно­ве вычисленной статистики DW Дарбина—Уотсона делается вы­вод об автокорреляции.

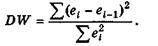
необходимым условием независимости слу­чайных отклонений является близость к двойке значения статистики Дарбина—Уотсона.

Не обращаясь к таблице критических точек Дарбина—Уотсона, можно пользоваться «грубым» правилом и считать, что авто­корреляция остатков отсутствует, если

1,5 < DW < 2,5. Для бо­лее надежного вывода целесообразно обращаться к табличным значениям.