Первый закон Кирхгофа в комплексной форме

Алгебраическая сумма комплексных действующих значений токов в узле равна нулю.

Второй закон Кирхгофа в комплексной форме

В замкнутом контуре электрической цепи алгебраическая сумма комплексных действующих значений ЭДС равна алгебраической сумме комплексных падений напряжений в нём.

1. Расчет сложных электрических цепей в комплексной форме.

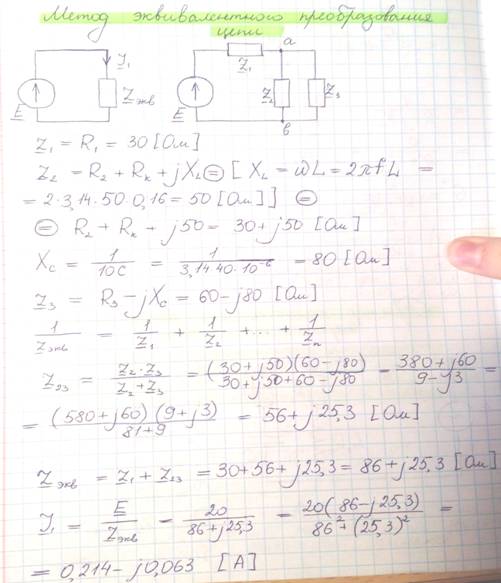
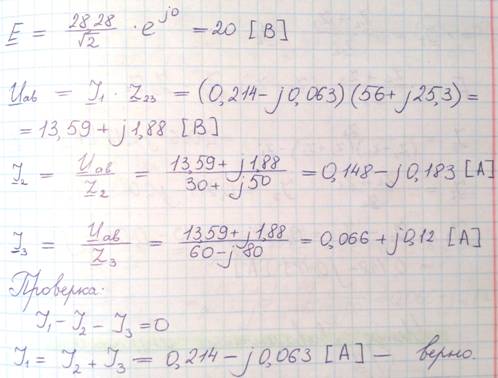
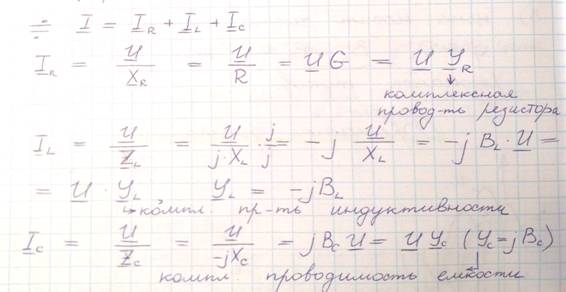1. Комплексное сопротивление. Комплексная проводимость.

30. Эквивалентное преобразование последовательного соединения в параллельное.

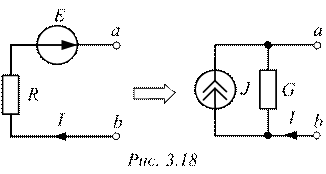
Эквивалентное преобразование последовательного соединения Е и R в параллельное соединение J и G

По второму закону Кирхгофа для схемы с последовательным соединением и по первому закону для схемы с параллельным соединением (рис. 3.18) можно записать:

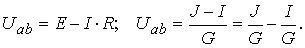
Эти выражения тождественны лишь при равенстве слагаемых, как не зависящих от тока I, так и пропорциональных ему. Поэтому

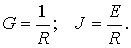
В обеих схемах сопротивление одинаково, а ЭДС и задающий ток источников связаны законом Ома.

31. Эквивалентное преобразование параллельного соединения в последовательное.

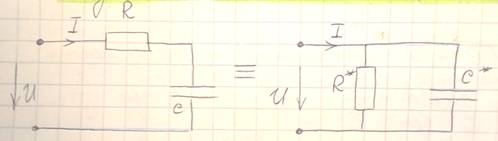
Участки цепи эквивалентны, если при одном и том же входном напряжении ток через эти участки одинаков.

; ;

; ;

; ;

;

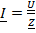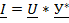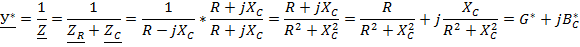
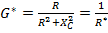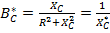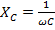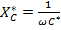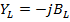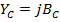
Примеры задач см. в конспекте.

32. Мощность в цепи синусоидального тока. Баланс мощностей.

1) Мгновенная мощность – произведение мгновенных значений напряжения и тока (или скорость изменения энергии источника)

;

;

;

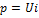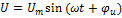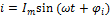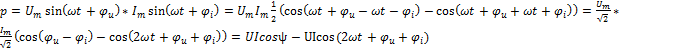– мгновенная мощность.

2) Активная мощностьР – среднее значение мгновенной мощности за период.

;

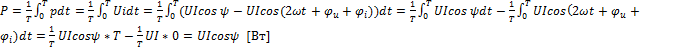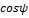– коэффициент мощности.

Активная мощность – мощность тепловых потерь на активном сопротивлении, т.к.:

;

;

;

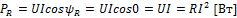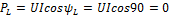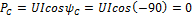Так как 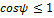, то активная мощность 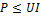. Чем ближе 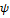к нулю, тем больше при заданых значениях 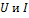активная мощность, передаваемая от источника к приемнику, и тем больше полезная работа совершается в цепи потребителя.

3) Реактивная мощность 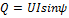[ВАР] (вольт-ампер реактивный)

;

;

;

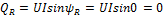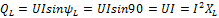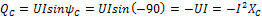Таким образом, активная мощность всегда положительна, поскольку cos – функция четная, то реактивная мощность может быть:

А) Q ≥ 0 для цепей активно-индуктивного характера (или чисто активного при );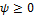

Б) Q< 0 для цепей активно-емкостного характера ( ).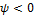

4) Полная мощность 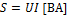(вольт-ампер)

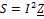
5) Комплексная мощность – это произведение комплексного действующего значения напряжения комплексного сопряженного действующего значения тока.

;

;

;

;

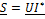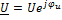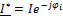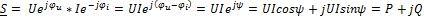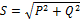–полная мощность,

.

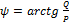Баланс мощностей.

Из закона сохранения энергии следует, что для любой электрической цепи соблюдается баланс активной и реактивной мощностей: сумма активных мощностей, генерируемых источниками, равна сумме активных мощностей, потребляемых всеми приемниками,

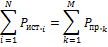
а сумма реактивных мощностей, отдаваемых источниками равна сумме реактивных мощностей, потребляемых приемниками.

;

;

;

; ;

;

;

;

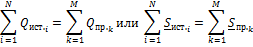
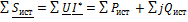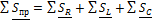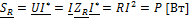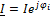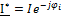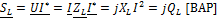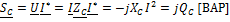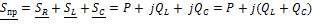Проверка правильности определения токов в цепи может быть осуществлена только при помощи баланса мощностей.

1. Резонанс напряжений.

Когда разность фаз 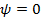, цепь носит чисто активный характер, и входное напряжение совпадает с током по фазе:

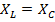
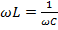­ условие резонанса напряжений

(возникает при последовательном соединении пассивных элементов R, L, C).

1. Резонанс токов.

Когда разность фаз 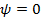, цепь носит чисто активный характер, и входное напряжение совпадает с током по фазе:

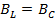­ условие резонанса токов

(возникает при параллельном соединении пассивных элементов R, L, C).

1. ЭДС самоиндукции и ЭДС взаимоиндукции. Их направления.

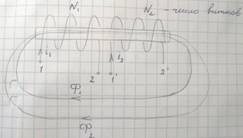С каждым витком катушки индуктивности связано магнитное поле, и при изменении этого поля во времени в витке по закону электромагнитной индукции наводится ЭДС, величина которой зависит только от скорости изменения магнитного потока и не зависит от причины, вызывающей ее изменение. Если изменение магнитного потока вызывается током, проходящим в этом витке, то имеет место явление самоиндукции. Если же его изменение вызвано током другого элемента, то имеет место явление взаимной индукции. Цепи, в которых есть взаимная индукция, называются индуктивно связанными цепями.

,

,

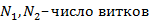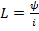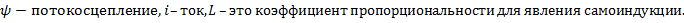
Для явления взаимной индукции коэффициентом пропорциональности М называется отношение потокосцепления взаимной индукции одной катушки к току, протекающему в другой катушке.

; ;

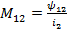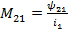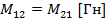
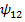– потокосцепление в первой катушке, вызванное током во второй катушке.

; ; ; ,

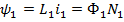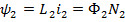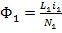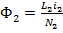где 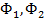– магнитные потоки, создаваемые токами, протекающими соответственно в первой и второй катушках. Переходя к рассмотрению потока взаимной индукции, имеем:

; ; ; .

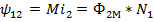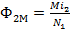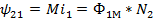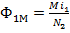Степень индуктивной связи двух катушек характеризуется коэффициентом связи

;

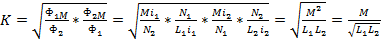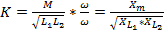, где 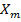– реактивное сопротивление взаимной индукции.

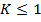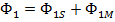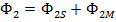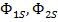Коэффициент , так как ; ; где – магнитные потоки рассеивания.

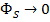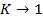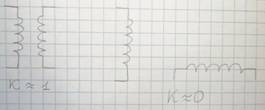
Если , тогда . Величина 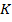зависит от взаимного расположения катушек индуктивности:

Таким образом, в каждой из двух индуктивно связанных катушек полный магнитный поток, пронизывающий витки этой катушки, включает в себя как поток самоиндукции, создаваемый током, протекающим в самой катушке, так и поток взаимной индукции, создаваемый током, протекающим в другой катушке.