Сопротивление в цепи синусоидального тока. Тригонометрическая форма расчета.

Метод контурных токов.

Метод является рациональным, удобным и наглядным методом расчета электрических цепей. Он основан на введении в расчет теоретического понятия контурных токов, т.е. токов, замыкающихся в независимых контурах. Число уравнений, необходимых для расчета по методу контурных токов определяется формулой p-q+1 = n, n – число независимых контуров. Задаваясь положительным направлением токов (выбирая направление обхода контура), записываем n уравнений по II закону Кирхгофа, и затем, решив полученную систему из n уравнений, находим значение контурных токов.

Обозначение: I₁₁, I₂₂,…,I_nn.

Искомые токи в ветвях определяются как алгебраическая сумма контурных токов, протекающих в соответствующей ветви, причем ток в ветви, в которой протекает только один контурный ток, равен этому контурному току.

Каждое из nуравнений для своего независимого контура составляется по правилу: «Контурный ток своего независимого контура умножается на сумму собственных сопротивлений, входящих в этот контур, а остальные слагаемые в левой части уравнения представляют собой произведение контурных токов других смежных контуров, имеющих общие ветви с рассматриваемым контуром, на сумму сопротивлений этих общих ветвей». Эти слагаемые записываются со знаком «+», если направление соседних контурных токов совпадает с направлением рассматриваемого контурного тока через смежную ветку, в противном случае с «–». Правая часть уравнений представляет собой алгебраическую сумму ЭДС, входящих в этот контур: «+», если стрелка ЭДС совпадает с направлением рассматриваемого контурного тока, иначе «–».

Пример 1.

;

;

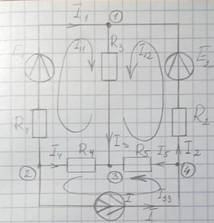
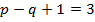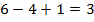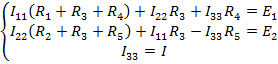
В схемах с источником тока выбор контурного тока должен осуществляться так, чтобы через ветку с источником тока проходил только один контурный ток.

; ; ; ; .

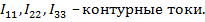
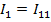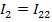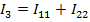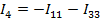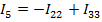Пример 2.

;

; ; ; ; .

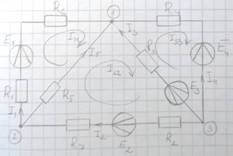
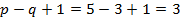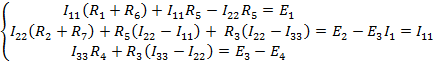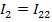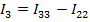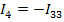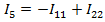12. Метод узловых потенциалов.

Метод базируется на введении понятия узловых напряжений, т.е. напряжений, действующих между каждым (q-1) независимым узлом и одним, произвольно выбранным, базисным (опорным) узлом, потенциал которого условно равен нулю. Число уравнений, необходимых для расчета по методу узловых потенциалов определяется формулой (q-1), q– число узлов. Этот метод позволяет ограничиться совместным решением (q-1) числа уравнений, записанных по Iзакону Кирхгофа для узловых напряжений (потенциалов узлов в схеме). В результате решения этой системы находим значения узловых напряжений (потенциалов узлов схемы).

…

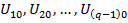
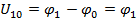
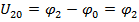
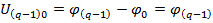
Искомые токи в ветвях определяются по закону Ома (для активных и пассивных участков цепи). Каждое из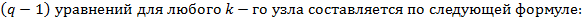

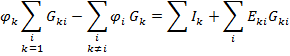
1) Слагаемое 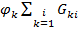– произведение узлового потенциала узла kи суммы проводимостей ветвей, сходящихся в этом узле.

2) 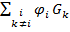– сумма произведений потенциалов всех остальных узлов схемы и суммы проводимостей ветвей, которыми они соединены с узлом k. Эти слагаемые всегда берутся со знаком «–».

Число слагаемых в правой части уравнения определяется числом активных ветвей, сходящихся в узле k.

3) 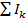–алгебраическая сумма токов источников тока, присоединенных к k-му узлу.

4) 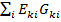– алгебраическая сумма произведений ЭДС ветвей, сходящихся в k-м узле и проводимостей этих ветвей.

Если стрелка ЭДС и стрелка источника тока направлены к узлу, то их значение в правой части записывается с «+», иначе с «–».

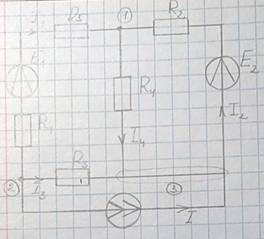
q–1=2

Пусть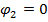

Для 1-го и 3-го узлов: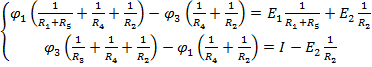

Проводимость источника тока = 0, R = ∞.

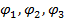находим из системы, далее по закону Ома находим истинные токи в ветвях.

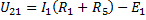, отсюда

;

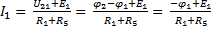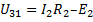, отсюда

;

;

;

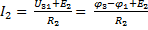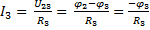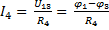По I закону Кирхгофа для 1-го и 2-го узлов имеем (*):

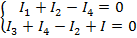
Выразив каждый из токов по закону Ома для активного или пассивного участка цепи, подставим эти токи в (*) и приведем полученную систему уравнений к первоначальной форме. Метод узловых потенциалов особенно удобен для расчета схем с двумя узлами.

13. Принцип и метод эквивалентного источника.

Метод основан на теореме об эквивалентном источнике.

Теорема: ток в любой ветви не изменится, если активный двухполюсник по отношению к рассматриваемой ветви заменить эквивалентным источником напряжения, ЭДС которого равна напряжению холостого хода на зажимах этой ветви, а внутренне сопротивление равно входному сопротивлению двухполюсника относительно этих же зажимов.

Двухполюсник - цепь, рассмотренная по отношению к одной паре зажимов, называемой входом двухполюсника.

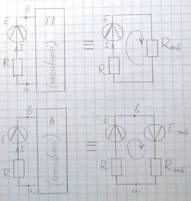Метод эквивалентного источника особенно удобен, если нужно найти ток только в одной ветви.

Сущность метода заключается в том, что по отношению к ветви с искомым током, вся остальная часть цепи рассматривается как активный двухполюсник, и в расчетах может быть заменена одним эквивалентным реальным источником ЭДС, т.е. ветвью с последовательным соединением ЭДС и R. Дополняя эту ветвь ветвью с искомым током, получаем одноконтурную простую схему. Ток в этой схеме, следовательно, и искомый ток в ветви определяется по II закону Кирхгофа.

Возможны два случая:

1) Ветвь с искомым током – пассивная. 2) Ветвь с искомым током – активная.

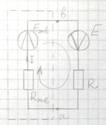
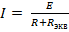
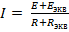
В полученных выражениях неизвестны 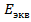и .

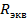Для определения 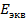нужно рассматривать активную схему, которая получается из заданной путем удаления из нее ветви с искомым током. Определив в этой новой активной схеме напряжение 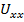(холостого хода) относительно разомкнутых зажимов, к которым в исходной схеме подключена ветвь с искомым током, т.е. найдя напряжение 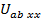, мы тем самым найдем 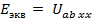(на основании теоремы об эквивалентном источнике). Стрелку 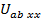на разомкнутой ветви следует направить также, как направлена стрелка тока в исследуемой ветви.

Для определения 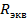рассматривают пассивную схему, которую получают из предыдущей, активной, устраняя из нее источники (закорачивание ветвей, содержащих идеальный источник ЭДС и разрывом ветвей с идеальным источником тока).

Определив в этой пассивной цепи сопротивление относительно разомкнутых зажимов, к которым подключена ветвь с искомым током в исходной схеме, т.е найдя 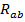, найдем 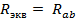(на основании теоремы об эквивалентном источнике).

Найденные выражения для 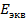и 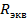подставляем в формулы для токов.

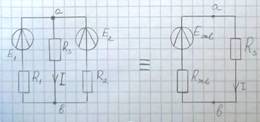Пример.

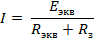
Для определения 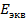и 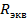удаляем ветку с искомым током.

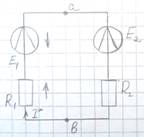
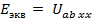
По II закону Кирхгофа: 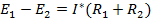, откуда ;

;

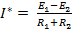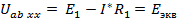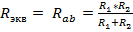; подставим в формулу для тока (примеры см. в конспекте).

14. Среднее и действующее значение синусоидального тока.

Синусоидальными называются периодические ЭДС, напряжения и токи, которые изменяются по синусоидальному закону.

; ; ;

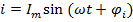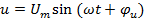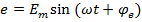i, u, e– мгновенные значения тока, напряжения и ЭДС, 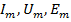– амплитуды синусоид,

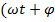) – фаза синусоиды,

Фаза определяет значение тока, напряжения и ЭДС в момент времени t,

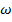[c^-1] – угловая (круговая) частота или скорость изменения аргумента синусоиды: .

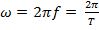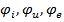– начальные фазы функций тока, напряжения и ЭДС, которые определяют величину смещения синусоиды относительно начала координат.

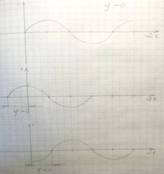Разность начальных фаз синусоид напряжения и тока называется фазовым сдвигом тока относительно напряжения: ψ = .

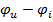Разность фаз (или фазовый сдвиг) положительный, если напряжение опережает ток (начальная фаза напряжения больше начальной фазы тока).

Сдвиг фаз отрицательный, если ток опережает напряжение (напряжение отстает от тока), т.е. начальная фаза напряжения меньше начальной фазы тока. Из двух синусоид опережает та, которая левее.

Действующее и среднее значение синусоидальной функции.

Очень часто при сравнении синусоидальных функций пользуются интегральными характеристиками.

1) Действующее значение синусоидальной функции – среднеквадратическое значение периодической функции. Она служит для сравнения их действия.

;

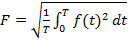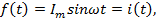I – действующее значение тока;

; .

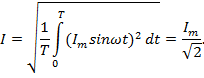
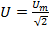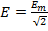Действующее значение функции тока численно равно значению постоянного тока, который протекает по сопротивлению, и за какой-то период времени выделит такое количество тепла, которое выделит синусоидальный ток в том же сопротивлении за то же время.

2) Среднее значение периодической функции за период:

; ; .

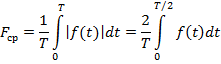
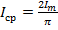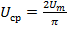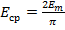15. Формы представления гармонической функции.

Представление синусоидальной функции с помощью комплексных чисел.

Существенные упрощения достигаются, когда расчет из области вещественной переменной переносится в область комплексного переменного, т.е. когда синусоидальная функция времени обозначается (изображается) комплексным числом.

Примечание: формы записи комплексных чисел.

Каждой точке на комплексной плоскости соответствует комплексное число, записанное в показательной, тригонометрической, алгебраической или полярной формах.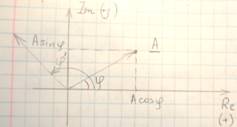

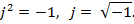
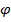– угол, отсчитываемый от оси действительных чисел;

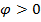, если отсчитывается против часовой стрелки;

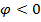, если отсчитывается по часовой стрелке;

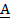– комплексное число;

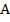– модуль (длина вектора) комплексного числа.

1) Полярная форма записи комплексного числа: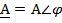

2) Показательная форма записи: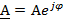

В показательной форме удобнее всего умножать и делить комплексные числа.

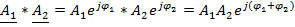
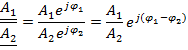
3) Тригонометрическая форма записи получается по формуле Эйлера:

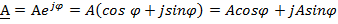
4) Алгебраическая форма записи:

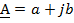(удобнее производить сложение и вычитание)

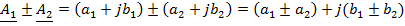
Баланс мощностей.

Из закона сохранения энергии следует, что для любой электрической цепи соблюдается баланс активной и реактивной мощностей: сумма активных мощностей, генерируемых источниками, равна сумме активных мощностей, потребляемых всеми приемниками,

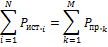
а сумма реактивных мощностей, отдаваемых источниками равна сумме реактивных мощностей, потребляемых приемниками.

;

;

;

; ;

;

;

;

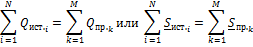
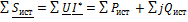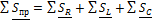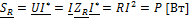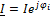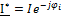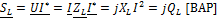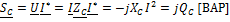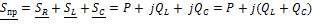Проверка правильности определения токов в цепи может быть осуществлена только при помощи баланса мощностей.

1. Резонанс напряжений.

Когда разность фаз 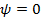, цепь носит чисто активный характер, и входное напряжение совпадает с током по фазе:

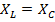
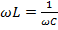­ условие резонанса напряжений

(возникает при последовательном соединении пассивных элементов R, L, C).

1. Резонанс токов.

Когда разность фаз 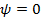, цепь носит чисто активный характер, и входное напряжение совпадает с током по фазе:

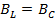­ условие резонанса токов

(возникает при параллельном соединении пассивных элементов R, L, C).

1. ЭДС самоиндукции и ЭДС взаимоиндукции. Их направления.

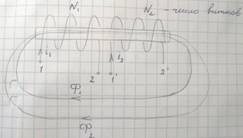С каждым витком катушки индуктивности связано магнитное поле, и при изменении этого поля во времени в витке по закону электромагнитной индукции наводится ЭДС, величина которой зависит только от скорости изменения магнитного потока и не зависит от причины, вызывающей ее изменение. Если изменение магнитного потока вызывается током, проходящим в этом витке, то имеет место явление самоиндукции. Если же его изменение вызвано током другого элемента, то имеет место явление взаимной индукции. Цепи, в которых есть взаимная индукция, называются индуктивно связанными цепями.

,

,

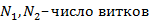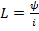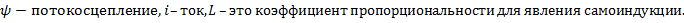
Для явления взаимной индукции коэффициентом пропорциональности М называется отношение потокосцепления взаимной индукции одной катушки к току, протекающему в другой катушке.

; ;

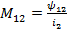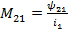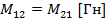
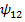– потокосцепление в первой катушке, вызванное током во второй катушке.

; ; ; ,

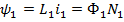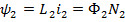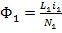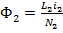где 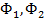– магнитные потоки, создаваемые токами, протекающими соответственно в первой и второй катушках. Переходя к рассмотрению потока взаимной индукции, имеем:

; ; ; .

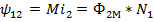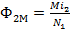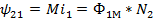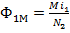Степень индуктивной связи двух катушек характеризуется коэффициентом связи

;

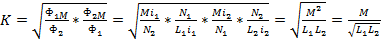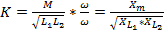, где 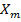– реактивное сопротивление взаимной индукции.

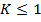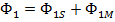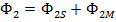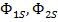Коэффициент , так как ; ; где – магнитные потоки рассеивания.

Если 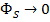, тогда 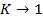. Величина 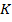зависит от взаимного расположения катушек индуктивности:

Таким образом, в каждой из двух индуктивно связанных катушек полный магнитный поток, пронизывающий витки этой катушки, включает в себя как поток самоиндукции, создаваемый током, протекающим в самой катушке, так и поток взаимной индукции, создаваемый током, протекающим в другой катушке.

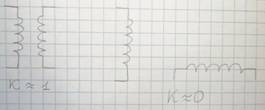
Однополярные зажимы.

Направление магнитного потока определяется по правилу правой руки:

«Пальцы правой руки направлены по току через катушку, ладонь охватывает сердечник как виток, большой палец указывает направление магнитного потока».

1 и 1’; 2 и 2’ – одноименные зажимы.

Если измерить напряжение обмотки любой катушки, тогда одноименными зажимами будут 1 и 2’; 2 и 1’, так как при одинаковом направлении токов относительно этих зажимов (втекает/вытекает) будут создаваться магнитные потоки, направленные в одну сторону.

Очевидно, что полное потокосцепление определяется полным магнитным потоком в каждой из двух индуктивно связанных катушек и состоит из потокосцепления самоиндукции ( 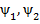) и потокосцепления взаимной индукции ( ).

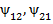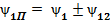, 1 – где, 2 – откуда,

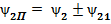
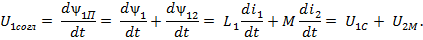
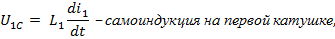
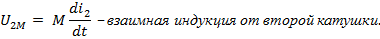
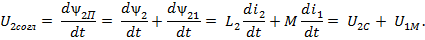
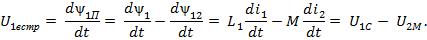
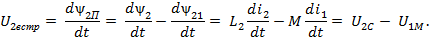
Переходя к комплексным числам, получим:

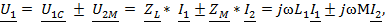
«+» - согласное включение, «–» - встречное включение.

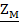– комплексное сопротивление взаимной индукции.

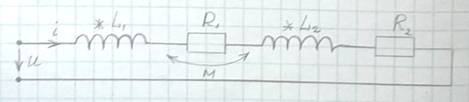38. Последовательное включение индуктивно связанных катушек.

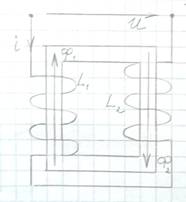Магнитные потоки Ф₁и Ф₂ складываются, соответственно катушки соединены согласно.

Электрическая схема данной цепи:

R₁, R₂ – активное сопротивление катушек (сопротивление проводов).

IIзакон Кирхгофа для данной схемы в комплексной форме:

= ,

;

= .

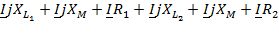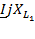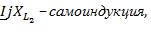
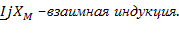
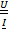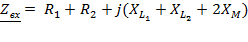При последовательном встречном включении расчеты аналогичны, только направление от взаимной индукции в уравнениях берется со знаком «–»:

= ,

= .

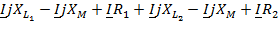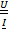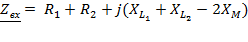Линейный трансформатор.

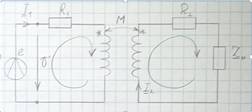
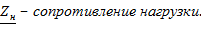
Левый контур не связан с правым контактом электрически (гальванически). Ток 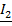в правом контуре существует в том случае, когда магнитные поля индуктивносте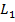й и 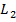оказываются связанными. Тогда изменение поля индуктивности 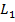, вызываемое протеканием синусоидального тока 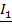будет сопровождаться наведением ЭДС взаимной индукции в индуктивности 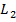, что и является причиной возникновения тока 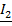во втором контуре. В свою очередь протекание тока 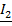будет сопровождаться наведением ЭДС взаимной индукции в индуктивности 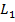. При этом, т.к. энергии передается во вторичный контур только наведением ЭДС взаимной индукции, то согласно правилу Ленца ток во втором контуре будет ослаблять вызвавшее его поле индуктивности первичного контура, т.е. напряжение первичного и вторичного токов при трансформаторном включении всегда будет встречным.

Запишем уравнение для каждого контура по IIзакону Кирхгофа:

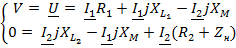
Из (2) получим: 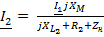, подставим в (1):

.

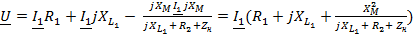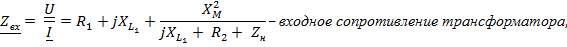
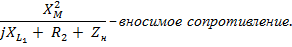
Метод контурных токов.

Метод является рациональным, удобным и наглядным методом расчета электрических цепей. Он основан на введении в расчет теоретического понятия контурных токов, т.е. токов, замыкающихся в независимых контурах. Число уравнений, необходимых для расчета по методу контурных токов определяется формулой p-q+1 = n, n – число независимых контуров. Задаваясь положительным направлением токов (выбирая направление обхода контура), записываем n уравнений по II закону Кирхгофа, и затем, решив полученную систему из n уравнений, находим значение контурных токов.

Обозначение: I₁₁, I₂₂,…,I_nn.

Искомые токи в ветвях определяются как алгебраическая сумма контурных токов, протекающих в соответствующей ветви, причем ток в ветви, в которой протекает только один контурный ток, равен этому контурному току.

Каждое из nуравнений для своего независимого контура составляется по правилу: «Контурный ток своего независимого контура умножается на сумму собственных сопротивлений, входящих в этот контур, а остальные слагаемые в левой части уравнения представляют собой произведение контурных токов других смежных контуров, имеющих общие ветви с рассматриваемым контуром, на сумму сопротивлений этих общих ветвей». Эти слагаемые записываются со знаком «+», если направление соседних контурных токов совпадает с направлением рассматриваемого контурного тока через смежную ветку, в противном случае с «–». Правая часть уравнений представляет собой алгебраическую сумму ЭДС, входящих в этот контур: «+», если стрелка ЭДС совпадает с направлением рассматриваемого контурного тока, иначе «–».

Пример 1.

;

;

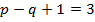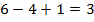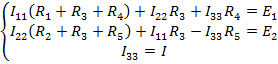
В схемах с источником тока выбор контурного тока должен осуществляться так, чтобы через ветку с источником тока проходил только один контурный ток.

; ; ; ; .

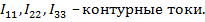
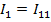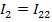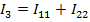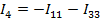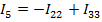Пример 2.

;

; ; ; ; .

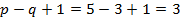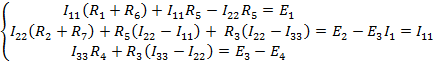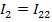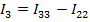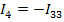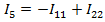12. Метод узловых потенциалов.

Метод базируется на введении понятия узловых напряжений, т.е. напряжений, действующих между каждым (q-1) независимым узлом и одним, произвольно выбранным, базисным (опорным) узлом, потенциал которого условно равен нулю. Число уравнений, необходимых для расчета по методу узловых потенциалов определяется формулой (q-1), q– число узлов. Этот метод позволяет ограничиться совместным решением (q-1) числа уравнений, записанных по Iзакону Кирхгофа для узловых напряжений (потенциалов узлов в схеме). В результате решения этой системы находим значения узловых напряжений (потенциалов узлов схемы).

…

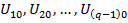
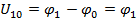
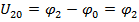
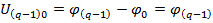
Искомые токи в ветвях определяются по закону Ома (для активных и пассивных участков цепи). Каждое из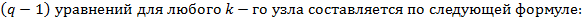

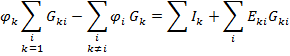
1) Слагаемое 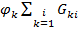– произведение узлового потенциала узла kи суммы проводимостей ветвей, сходящихся в этом узле.

2) 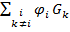– сумма произведений потенциалов всех остальных узлов схемы и суммы проводимостей ветвей, которыми они соединены с узлом k. Эти слагаемые всегда берутся со знаком «–».

Число слагаемых в правой части уравнения определяется числом активных ветвей, сходящихся в узле k.

3) 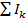–алгебраическая сумма токов источников тока, присоединенных к k-му узлу.

4) 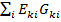– алгебраическая сумма произведений ЭДС ветвей, сходящихся в k-м узле и проводимостей этих ветвей.

Если стрелка ЭДС и стрелка источника тока направлены к узлу, то их значение в правой части записывается с «+», иначе с «–».

q–1=2

Пусть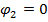

Для 1-го и 3-го узлов: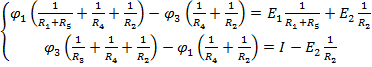

Проводимость источника тока = 0, R = ∞.

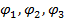находим из системы, далее по закону Ома находим истинные токи в ветвях.

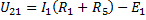, отсюда

;

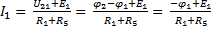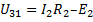, отсюда

;

;

;

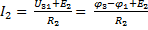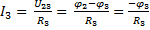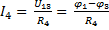По I закону Кирхгофа для 1-го и 2-го узлов имеем (*):

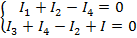
Выразив каждый из токов по закону Ома для активного или пассивного участка цепи, подставим эти токи в (*) и приведем полученную систему уравнений к первоначальной форме. Метод узловых потенциалов особенно удобен для расчета схем с двумя узлами.

13. Принцип и метод эквивалентного источника.

Метод основан на теореме об эквивалентном источнике.

Теорема: ток в любой ветви не изменится, если активный двухполюсник по отношению к рассматриваемой ветви заменить эквивалентным источником напряжения, ЭДС которого равна напряжению холостого хода на зажимах этой ветви, а внутренне сопротивление равно входному сопротивлению двухполюсника относительно этих же зажимов.

Двухполюсник - цепь, рассмотренная по отношению к одной паре зажимов, называемой входом двухполюсника.

Метод эквивалентного источника особенно удобен, если нужно найти ток только в одной ветви.

Сущность метода заключается в том, что по отношению к ветви с искомым током, вся остальная часть цепи рассматривается как активный двухполюсник, и в расчетах может быть заменена одним эквивалентным реальным источником ЭДС, т.е. ветвью с последовательным соединением ЭДС и R. Дополняя эту ветвь ветвью с искомым током, получаем одноконтурную простую схему. Ток в этой схеме, следовательно, и искомый ток в ветви определяется по II закону Кирхгофа.

Возможны два случая:

1) Ветвь с искомым током – пассивная. 2) Ветвь с искомым током – активная.

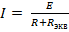
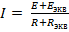
В полученных выражениях неизвестны 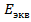и .

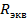Для определения 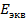нужно рассматривать активную схему, которая получается из заданной путем удаления из нее ветви с искомым током. Определив в этой новой активной схеме напряжение 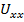(холостого хода) относительно разомкнутых зажимов, к которым в исходной схеме подключена ветвь с искомым током, т.е. найдя напряжение 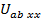, мы тем самым найдем 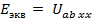(на основании теоремы об эквивалентном источнике). Стрелку 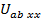на разомкнутой ветви следует направить также, как направлена стрелка тока в исследуемой ветви.

Для определения 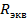рассматривают пассивную схему, которую получают из предыдущей, активной, устраняя из нее источники (закорачивание ветвей, содержащих идеальный источник ЭДС и разрывом ветвей с идеальным источником тока).

Определив в этой пассивной цепи сопротивление относительно разомкнутых зажимов, к которым подключена ветвь с искомым током в исходной схеме, т.е найдя 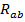, найдем 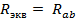(на основании теоремы об эквивалентном источнике).

Найденные выражения для 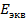и 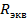подставляем в формулы для токов.

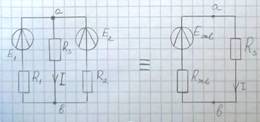Пример.

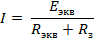
Для определения 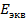и 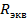удаляем ветку с искомым током.

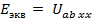
По II закону Кирхгофа: 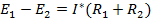, откуда ;

;

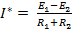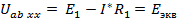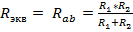; подставим в формулу для тока (примеры см. в конспекте).

14. Среднее и действующее значение синусоидального тока.

Синусоидальными называются периодические ЭДС, напряжения и токи, которые изменяются по синусоидальному закону.

; ; ;

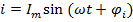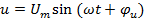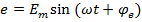i, u, e– мгновенные значения тока, напряжения и ЭДС, 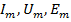– амплитуды синусоид,

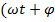) – фаза синусоиды,

Фаза определяет значение тока, напряжения и ЭДС в момент времени t,

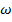[c^-1] – угловая (круговая) частота или скорость изменения аргумента синусоиды: .

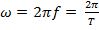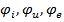– начальные фазы функций тока, напряжения и ЭДС, которые определяют величину смещения синусоиды относительно начала координат.

Разность начальных фаз синусоид напряжения и тока называется фазовым сдвигом тока относительно напряжения: ψ = .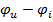

Разность фаз (или фазовый сдвиг) положительный, если напряжение опережает ток (начальная фаза напряжения больше начальной фазы тока).

Сдвиг фаз отрицательный, если ток опережает напряжение (напряжение отстает от тока), т.е. начальная фаза напряжения меньше начальной фазы тока. Из двух синусоид опережает та, которая левее.

Действующее и среднее значение синусоидальной функции.

Очень часто при сравнении синусоидальных функций пользуются интегральными характеристиками.

1) Действующее значение синусоидальной функции – среднеквадратическое значение периодической функции. Она служит для сравнения их действия.

;

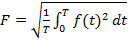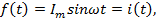I – действующее значение тока;

; .

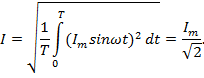
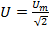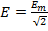Действующее значение функции тока численно равно значению постоянного тока, который протекает по сопротивлению, и за какой-то период времени выделит такое количество тепла, которое выделит синусоидальный ток в том же сопротивлении за то же время.

2) Среднее значение периодической функции за период:

; ; .

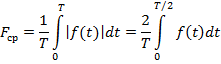
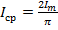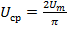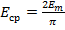15. Формы представления гармонической функции.

Представление синусоидальной функции с помощью комплексных чисел.

Существенные упрощения достигаются, когда расчет из области вещественной переменной переносится в область комп