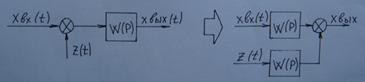
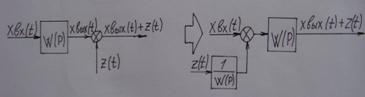
Пребразование структурных схем.

Классификация САУ

САУ

обыкновенные

адаптивные

игровые

С обратной связью

разомкнутые

Системы экстренного регулирования

Самонастраиваемые системы

Системы с набором шаблонного решения

Системы с автоматическим поиском решения

следящие

стабилизирующие

Системы с компенсацией

Системы программного управления

Комбинированные САУ

Приведенная выше классификация САУ не исчерпывает всего многообразия существующих в настоящее время САУ. Если выбрать другие классификационные признаки, то САУ можно разделить на: непрерывные и дискретные, линейные и нелинейные, стационарные и нестационарные, детерминированные и стохастические, одноконтурные и многоконтурные.

В зависимости от ошибки в установившемся режиме при постоянном внешнем воздействии(управляющим или возмущающим) САУ подразделяются на статические и астатические.

Динамическая ошибка системы определяется следующим образом: E(t) = Xвх(t) – Xвых(t)

При установившихся значениях Xвх уст(t), Xвых уст(t), можно найти установившуюся ошибку системы: Eуст = Xвх уст – Xвых уст

САУ называют статической по отношению к установившемуся значению, если при постоянном внешнем воздействии, которое с течением времени стремится к некоторому установившемуся значению, ошибка также стремится к постоянному значению, зависящему от величины управляющего воздействия.

У статических систем установившаяся ошибка не равна 0 (Еуст ≠ 0).

У астатических систем – (Еуст = 0)

Передаточная функция

Передаточная функция звена –символьная запись основных уравнений динамики звена.

Чтобы из уравнений можно было получить передаточную функцию звена, число переменных в них должно быть равно (n+1), где n – число уравнений. В число переменных входят вх. и вых. величины, а также могут входить промежуточные переменные. Для получения передаточной функции эти переменные должны быть исключены путем выражения переменной из одного уравнения и подстановкой в другое уравнение.

Передаточная функция –это отношение преобразования Лапласа выходной переменной к входной.

Передаточная функция – отношение изображения по Лапласу выходной величины системы (элемента) к изображению по Лапласу входной величины при нулевых начальных условиях.

Для её нахождения необходимо:

1) записать уравнение системы (элемента) в форме Лапласа при нулевых начальных условиях

2) найти отношение изображения выходной величины к изображению входной величины

В форме Лапласа дифференциальное уравнение:

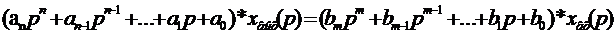
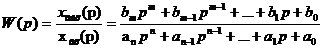
Пример:

Дифф.уравнение: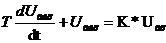

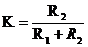- коэффициент передачи

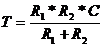- постоянная времени

В форме Лапласа: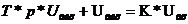

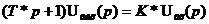
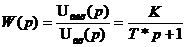
Типовые входные сигналы

Для исследования динамических свойств системы необходимо решить диффер-ое урав-ие . Эту задачу можно выполнить , если известен закон изменения во времени внешних воздействий . В общем случае внешнее воздействие имеют сложный хар-р и явл. Случайным . На практике , для оценки динамич. Св-в САУ и их эл-ов, ограничиваются несколькими типовыми воздействиями.

Единичная ступенчата функция.

Xвх(t)=1(t)

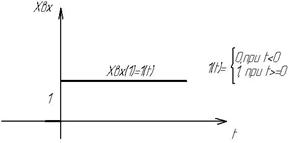
Ступенчая функция

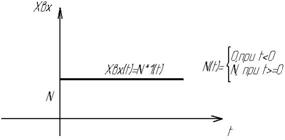
Такого вида воздействия сводятся к мгновенному изменению нагрузки электрического генератора и как следствие изменение нагрузки электрического двигателя.

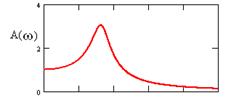
Колебательное звено

Дифференциальное уравнение звена :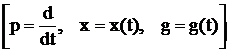

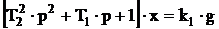
причем T₁<2T₂, так, что корни характеристического уравнения - комплексные.

Тогда уравнение можно переписать уравнение в форме

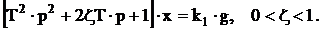
При ζ≥1 звено превращается в т.н. апериодическое звено второго порядка.

Пример колебательного звена – масса на упругом подвесе со слабым скоростным демпфировании (параметр β).

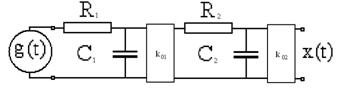
Апериодическое (инерционное) звено второго порядка

Апериодическое звено второго порядка – это последовательное соединение двух апериодических звеньев через звено, обеспечивающее направленность, в данном случае пропорциональное звено с усилением k₀₁.

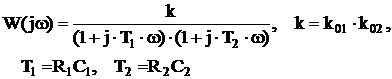
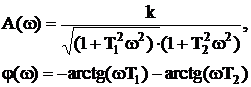
Далее:

ЛАЧХ, ЛФЧХ, реакция на 1(t), δ(t).

Надо отметить, что передаточная функция последовательного соединения типовых звеньев получается простым перемножением их передаточных функций. Имея передаточную функцию последовательного соединения легко записать дифференциальное уравнениеэтого соединения:

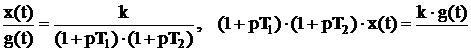
Откуда, после очевидных преобразований и обратной замены 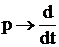, получим

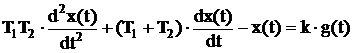
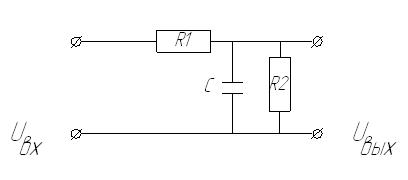
Примечание. Последовательное соединение двух RC- цепочек описывается

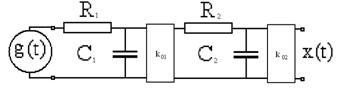
другим дифференциальным уравнением и обладает другими динамическими свойствами.

Примеры физических систем со свойствами апериодического звена второго порядка:

- два однозвенных RC-фильтра, разделенных усилителем;

- термопара в металлическом корпусе.

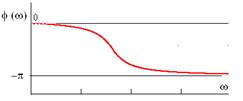
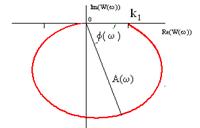
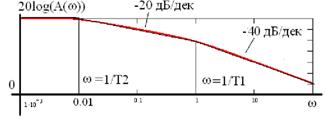
Логарифмическая амплитудная частотная характеристика (красный цвет) и ее аппроксимация асимптотами (черный цвет):

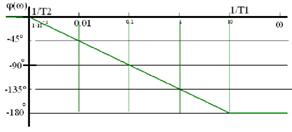
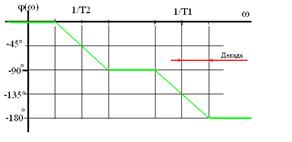
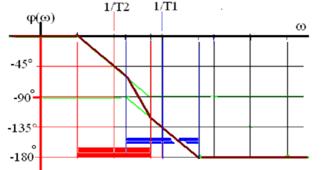
Логарифмическая фазовая частотная характеристика, аппроксимированная асимптотами, для различных значений постоянных времени:

- (1/T11-1/T21)=10⁴ , т.е. четыре декады;

- (1/T1-1/T2)>10⁴ - более четырех декад;

- (1/T1-1/T2)<10⁴ - менее четырех декад;

Дифференцирующие звено.

Идеальным ДЗ называется такое звено дифферинцирующего уравнения которое имеет вид:
X_вых = kX_вх(t) (1)

Выходная величина такого звена пропорциональна производной от входной величины.

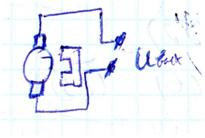
Единственным идеальным дефференцирующем звеном которое в полной мере описывает выражение (1) является тахогенератор постоянного тока.

Если в качестве входной величины рассматривать угол поворота ротора (φ) а в качестве выходной ЭДС якоря (Е). В тахогенераторе постоянного тока при неизменном потоке возбуждения ЭДС в якоре пропорционально скорости вращения.

В режиме близком к холостому ходу, когда сопротивление нагрузки не велико, можно считать что напряжение якоря равно ЭДС.

Е = V

W(iω) = ikω A(ω) = kω φ(ω) = +90° L(ω) = 20lgk + 20kgω

V = k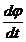

W(p) = kp

h(t) = k*1(t) = kδ(t)

ω(t) = kδ(t) =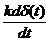

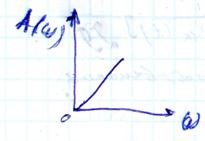
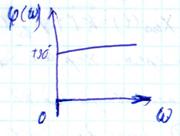
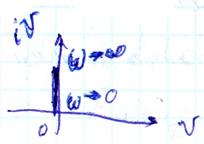
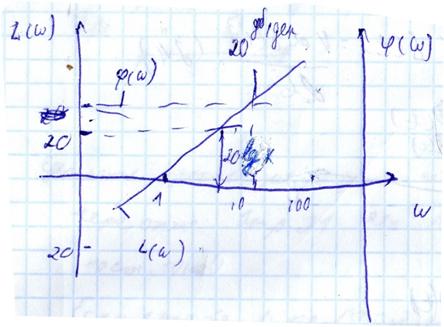
ЛЧХ идеального ДЗ обратны соответствующим характеристикам интегрирующего звена.

Понятие устойчивости САУ.

Определение устойчивостилинейной невозмущенной системы,то есть системы, при нулевом входном сигнале (g(t)º0).

Линейная невозмущенная система:

Линейная система устойчива, если переходный процесс в системе затухает с течением времени, т.е. если собственное (свободное) движение системы

x(t)→0 при t→ .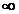

Под устойчивостью линейной системы понимают свойство затухания переходного процесса с течением времени.

Необходимое условие устойчивости - положительность всех коэффициентов характеристического уравнения. При n³3 оно недостаточно. Как будет показано ниже на ряде примеров САУ третьего порядка (n=3) может оказаться неустойчивой и при положительных коэффициентах дифференциального уравнения.

Если l_i=a_i+w_i - корень характеристического уравнения (i=1..n)

,

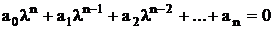то условие устойчивости системы - расположение корней характеристического уравнения в левой полуплоскости комплексного нпременного l (α_i<0).

Это очевидно из равенства

.

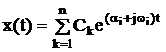(для упрощения предполагается, что у характеристического уравнения нет кратных корней).

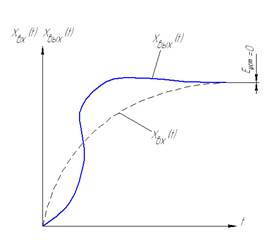
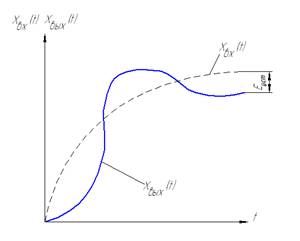
21.Переходные и установившиеся процессы.

Переходный процесс:

Переходный процесс характеризуется:

- Длительностью переходного процесса (t _п), то есть временем от начала переходного процесса до момента, начиная с которого выходная величина остается в пределах ±d% от установившегося значения (обычно, d%=±5%).

- Максимальным отклонением регулируемой величины (x_max) или величиной 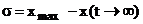) - перерегулированием. Перерегулирование может быть выражено в процентах от установившегося значения )

.

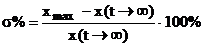Обычно перерегулирование лежит в пределах 10..30%, в некоторых случаях допускается перерегулирование до 70% [2].

- Временем нарастания выходного сигнала (t_н). В точке x(t)=x(t®¥)/2 строят касательную к x(t)и определяют временя нарастания, как показано на рис.1.

- Колебательностью, то есть числом колебаний, которое может наблюдаться в течение времени переходного процесса (обычно, 1..2 колебания, иногда - и 3..4 колебания). В некоторых с системах колебания на допускаются вообще [2].

Используются и другие критерии оценки переходных процессов (например, время запаздывания).

Те же критерии оценки применимы и для случая x(t®¥)=0.

Критерий устойчивости САУ.

В ТАУ разработан ряд правил, с помощью которых можно судить о знаках действительных

частей корней, не решая характеристическое уравнение и не находя числовые значения

самих корней. Эти правила получили название критериев устойчивости.

Различают алгебраические и частотные критерии устойчивости.

Алгебраические критерии устанавливают необходимые и достаточные условия

отрицательности корней в форме ограничений, накладываемых на определенные

комбинации коэффициентов характеристического уравнения системы.

Частотные критерии определяют связь между устойчивостью системы и формой ее частотных характеристик.

Понятие об устойчивости системы регулирования связано со способностью. Возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели её из этого состояния. Наглядно устойчивость равновесия можно проил-ть

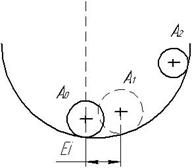В виде шара лежащего в некотором углублении .

При всяком отклонении его от положения равновесия, шар будет стремится вернуться к нему точно ( при отсутствии сил трения)или к некоторой конечной области, окружающ предшеств.равновесия обл-ти

( при наличии сил трения).Такое положение шара будет устойчивым.

Классификация САУ

САУ

обыкновенные

адаптивные

игровые

С обратной связью

разомкнутые

Системы экстренного регулирования

Самонастраиваемые системы

Системы с набором шаблонного решения

Системы с автоматическим поиском решения

следящие

стабилизирующие

Системы с компенсацией

Системы программного управления

Комбинированные САУ

Приведенная выше классификация САУ не исчерпывает всего многообразия существующих в настоящее время САУ. Если выбрать другие классификационные признаки, то САУ можно разделить на: непрерывные и дискретные, линейные и нелинейные, стационарные и нестационарные, детерминированные и стохастические, одноконтурные и многоконтурные.

В зависимости от ошибки в установившемся режиме при постоянном внешнем воздействии(управляющим или возмущающим) САУ подразделяются на статические и астатические.

Динамическая ошибка системы определяется следующим образом: E(t) = Xвх(t) – Xвых(t)

При установившихся значениях Xвх уст(t), Xвых уст(t), можно найти установившуюся ошибку системы: Eуст = Xвх уст – Xвых уст

САУ называют статической по отношению к установившемуся значению, если при постоянном внешнем воздействии, которое с течением времени стремится к некоторому установившемуся значению, ошибка также стремится к постоянному значению, зависящему от величины управляющего воздействия.

У статических систем установившаяся ошибка не равна 0 (Еуст ≠ 0).

У астатических систем – (Еуст = 0)

Передаточная функция

Передаточная функция звена –символьная запись основных уравнений динамики звена.

Чтобы из уравнений можно было получить передаточную функцию звена, число переменных в них должно быть равно (n+1), где n – число уравнений. В число переменных входят вх. и вых. величины, а также могут входить промежуточные переменные. Для получения передаточной функции эти переменные должны быть исключены путем выражения переменной из одного уравнения и подстановкой в другое уравнение.

Передаточная функция –это отношение преобразования Лапласа выходной переменной к входной.

Передаточная функция – отношение изображения по Лапласу выходной величины системы (элемента) к изображению по Лапласу входной величины при нулевых начальных условиях.

Для её нахождения необходимо:

1) записать уравнение системы (элемента) в форме Лапласа при нулевых начальных условиях

2) найти отношение изображения выходной величины к изображению входной величины

В форме Лапласа дифференциальное уравнение:

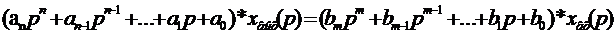
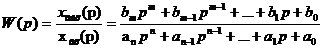
Пример:

Дифф.уравнение: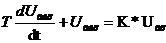

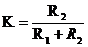- коэффициент передачи

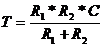- постоянная времени

В форме Лапласа: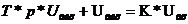

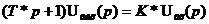
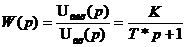
Пребразование структурных схем.

Математические модели САО в переменных вход-выход обычно представляют в

виде структурных схем. Эти схемы первоначально составляются в соответствие с

принципами функций системы.

Структурная схема – это графическое условное обозначение элементов или

звений,составляющих систему и различающихся своими динамическими свойствами.

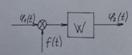
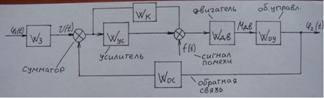
Преобразуем систему.

Следовательно необходимо производить эквивалентные преобразования

структурных схем (не нарушающие их динамических свойств).

Правила преобразования:

1.Последовательное соединение звеньев

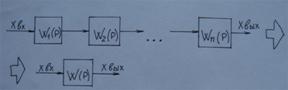
W(P)=W₁(P)*W₂(P)*....*W_n(P)

2.Параллельное соединение звеньев

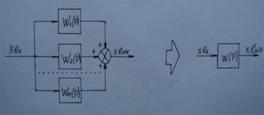
W(P)=W₁(P)+W₂(P)+....+W_n(P)

3.Контур с обратной связью

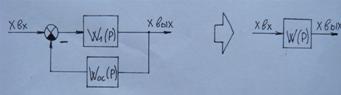
W(P)=W₁(P)/1±W₁(P)*W_oc(P)

4.Перенос узла(точка равновесия сигнала)

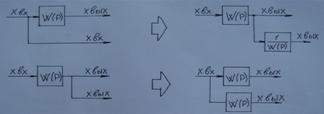
5.Перенос точек суммирования(сумматор)