Бесконечно большие и бесконечно малые функции.

Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Теорема. Если функция y=f(x) представима при x→aв виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то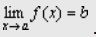

Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.

Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.

Функция называется бесконечно большой при x стремящееся a или в точке a, если для любого положительного числа e найдется такое положительное d(e), что для всех x удовлетворяющих условию |x-a|<d будет выполнено неравенство |f(x)|>e .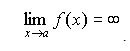

Свойства функций имеющих предел

Односторонние пределы функции в точке

Предел функции в бесконечности

Число А называется пределом функции f (x) при х → ∞, если для любого как угодно малого положительного числа ε, найдётся зависящее от этого ε большое положительное число К, такое, что для всех значений аргумента, больших по величине этого числа К, значения функции отличаются по величине от указанного числа А меньше, чем на ε:

( Аперевернутое ε > 0 ) ( Еперевернутое K = K ( ε ) > 0 ) ( Аперевернутое | x | > K ) : | f ( x ) − A | < ε.

Число В называется пределом функции f (x) при х → + ∞, если для любого как угодно малого положительного числа ε, найдётся зависящее от этого ε большое положительное число К, такое, что для всех значений аргумента, больших этого числа К, значения функции отличаются по величине от указанного числа В меньше, чем на ε:

( А перевернутое ε > 0 ) ( Е перевернутое K = K ( ε ) > 0 ) ( А перевернутое x > K ) : | f ( x ) − B | < ε.

Такие пределы символически имеют запись

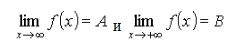
Предел функции f (x)при х → – ∞ формулируется аналогично: если для любого как угодно малого положительного числа ε, найдётся зависящее от этого ε большое отрицательное число К, такое, что для всех значений аргумента, меньших этого числа К, значения функции отличаются по величине от указанного числа В меньше, чем на ε.

Теоремы об арифметических действиях с пределами

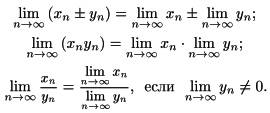Об арифметических действиях над сходящимися.

39

40

41. Определение производной

Производная как скорость изменения функции

Геометрический смысл производной

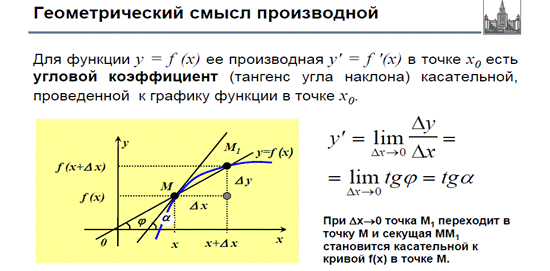
Связь между непрерывностью и существованием производной

Правило вычисления производной от суммы, произведения и частного функций

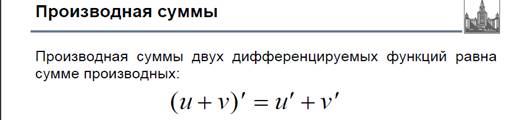
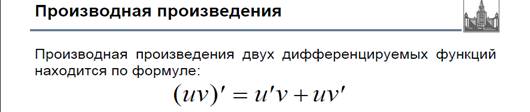
Производная сложной функции

Нахождение производных от основных элементарных функций

Бином Ньютона

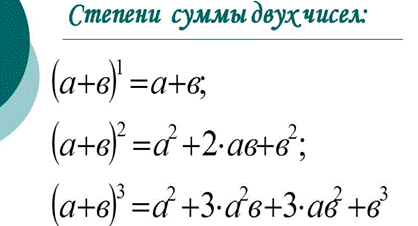
Теорема Лагранжа о конечном приращении функции на отрезке

Правила Лопиталя раскрытия неопределенностей

Понятие о дифференциале функции