Правило предельного перехода

Правило 1. Если функция f непрерывна в точке x₀, то Δf→0 при Δx→0.

Правило 2. Если функция f имеет производную в точке х₀, то Δf/Δx→f'(x₀) при Δx→0.

Правила 1 и 2 сразу следуют из определений непрерывности функции f в точке х₀ и производной в точке x₀.

Правило 3. Пусть f (x)→A, g{x)→B при x→x₀. Тогда при х→x₀ (т. е. при Δx→0):

а) f(x) + g(x)→A + B;

б) f(x)•g(x)→A•B;

в) f(x)/g(x)→A/B (при B≠0).

Для непрерывных функций f u g

А = f (х₀), В = g (х₀)

и эти правила означают, что сумма, произведение и частное непрерывных в точке хо функций непрерывны в точке х₀ (частное в случае, когда g(x₀)≠0).

Правила предельного перехода широко используются при доказательстве непрерывности функций и выводе формул дифференцирования.

Сравнение бесконечно малых величин

Определения. Пусть при 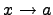функции f(x) и g(x) являются бесконечно малыми. Тогда:

1. Если 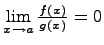, то f(x) называется бесконечно малой высшего порядка относительно g(x).

2. Если 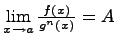(конечен и отличен от 0), то f(x) называется бесконечно малой n-го порядка относительно g(x).

3. Если 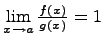, то f(x) и g(x) называются эквивалентными бесконечно малыми.Эквивалентность записывается так: .

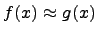Свойства эквивалентных бесконечно малых:

1. Разность двух эквивалентных бесконечно малых есть бесконечно малая высшего порядка относительно каждой из них.

2. Если из суммы нескольких бесконечно малых разных порядков отбросить бесконечно малые высших порядков, то оставшаяся часть, называемая главной, эквивалентна всей сумме.

Сравнение бесконечно больших величин

1) 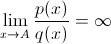, т.е. предел отношения функций существует и равен бесконечности. В этом случае говорят, что p(x) бесконечно большая функция более высокого порядка.

2) 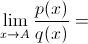, т.е. предел отношения функций существует и равен С - некоторой константе. В этом случае говорят, что p(x) и q(x) бесконечно большие функции одного порядка.

3) 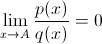, т.е. предел отношения функций существует и равен нулю. В этом случае говорят, что q(x) бесконечно большая функция более высокого порядка.

4) Если данный предел: 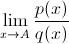не существует, в этом случае мы ничего не можем сказать о сравниваемых функциях и поэтому говорят, что функции не сравнимы.

Производная и ее геометрический смысл.

Производная - это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

Уравнение касательной и нормали к линии.

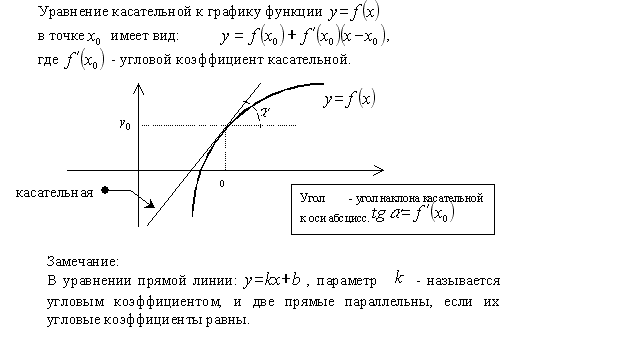
уравнение нормали

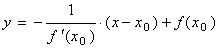
Производная сложной функции

Рассмотрим сложную функцию y = y(u(x))

Теорема 4. Если функции y = y(u), u = u(x) дифференцируемы (т.е. существуют производные y'_u, u'_x), тогда сложная функция y = y(u(x)) дифференцируема и y'_x = y'_u u'_x.

Доказательство

Если аргумент x получит приращение Δx, то функция u получит приращение Δu = u(x + Δx) − u(x), а функция y получит приращение Δy = y(u + Δu) − y(u). Но тогда, воспользовавшись свойствами предела функции, получаем

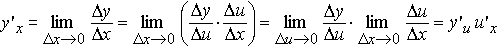
Теорема доказана.