Организация файлов. Общие сведения.

Файл - это поименованная область во внешней памяти.

Ранее, при обсуждении структур данных, предполагалось, чтообъем данных позволяет обходиться исключительно основной (оперативной) памятью. Существуют задачи, в которых объем используемых данных намного превышает возможности основной памяти. Вбольшинстве вычислительных систем предусмотрены устройствавнешней памяти (диски, ленты), на которых можно хранить огромные объемы данных.

Во многих языках программирования предусмотрен файловый типданных, предназначенный для представления данных, хранящихся вовнешней памяти. Даже если в языке программирования файловый типне определен, в операционной системе понятие файла, несомненно,поддерживается.

Операционная система делит внешнюю память на блоки одинакового размера. Размер блока зависит от конкретного типа операционнойсистемы. Файлы хранятся в виде определенной последовательности блоков; каждый такой блок содержит целое число записей файла.

Базовыми операциями, выполняемыми по отношению к файлам, является перенос одного блока из внешней памяти в буфер и перенос

Общие сведения:

Существуют несколько способов организации данных в виде файлов:
последовательный файл;
хешированные файлы;
индексированные файлы;
В-деревья.
Рассмотрим кратко первые три способа использования (В-деревья рассмотрим более подробно далее).
При простой (и наименее эффективной) организации данных в виде последовательных файлов используются такие примитивы чтения и записи файлов, которые встречаются во многих языках программирования (например, read() и write() в языке Паскаль). В этом случае записи могут храниться в любом порядке.
Поиск записи осуществляется путем полного просмотра файла. Вставку в файл можно выполнять путем присоединения соответствующей записи в конец файла. В случае изменения записи необходимо осуществить поиск требуемой записи, а затем внести в нее изменения.
При удалении записи тоже необходимо найти удаляемую запись, а затем определенным вариантом удалить. Один из вариантов - сдвинуть все записи, следовавшие за удаленной записью, на одну позицию вперед (осуществляя при сдвиге перенос записей между блоками). Однако такой подход не годится, если записи являются закрепленными, поскольку указатель наi-ю запись в файле после выполнения такой операции будет указывать на (i+1)-ю запись. В этом случае необходимо определенным образом помечать уделенные записи, но не смещать оставшиеся на место удаленных (и не должны вставлять на их место новые записи). Существуют два способа помечать удаленные записи:
1) заменить значение записи на специальное значение, которое никогда не может стать значением не удалённой записи;
2) предусмотреть для каждой записи специальный бит удаления, который содержит, например, 1 в удаленных записях и О - в не удалённых записях.
Очевидным недостатком последовательного файла является то, что операции с такими файлами выполняются медленно. Выполнение каждой операции требует, чтобы осуществлялось чтение всего файла. Однако существуют способы организации файлов, позволяющие обращаться к записи, считывая в основную память лишь небольшую часть файла. Такие способы предусматривают наличие у каждой записи файла так называемого ключа, т. е. поля (или совокупности полей), которое уникальным образом идентифицирует каждую запись. К сожалению, при отсутствии ключей, ускорения операций добиться не удается.
Хеширование - широко распространенный метод обеспечения быстрого доступа к информации, хранящейся во внешней памяти. Основная идея этого метода подобна методу цепочек, который рассматривается в 2.3.2. Только здесь, вместо записей таблицы организуется связный список блоков. Заголовок i-го блока содержит указатель на физический адрес (i+1)-го блока. Записи, хранящиеся в одном блоке, связывать друг с другом с помощью указателей не требуется. Сама таблица представляет собой таблицу указателей на блоки.

19. B-деревья. Основные определения и способы реализации

Как мы уже видели, очень эффективным является хранение множества данных в виде дерева. Поэтому в качестве типового способа организации внешней памяти стало В-дерево, которое обеспечивает при своем обслуживании относительно небольшое количество обращений к внешней памяти.
В-дерево представляет собой дерево поиска степени т, характеризующееся следующими свойствами:
1) корень либо является листом, либо имеет не менее двух потомков;
2) каждый узел, кроме корня и листьев, имеет от (т/2) до т потомков;
3) все пути от корня до любого листа имеют одинаковую длину.
В каждой вершине будем хранить не более NumberO f I tems записей. Также необходимо будет хранить текущее количество записей в вершине. Для удобства возврата назад к корню дерева будем запоминать для каждой вершины указатель на ее предка.
Основные операции, производимые с В-деревьями:
поиск элемента;
добавление элемента;
удаление элемента.
При рассмотрении этих основных операций будут разбираться небольшие деревья, хотя в реальности В-деревья применяются при работе с большими массивами информации. Кроме того, для наглядности, на рисунках будут опускаться поля указателей.
поиск элемента будем начинать с корневой вершины. Если искомый элемент присутствует в загруженной вершине, то завершаем поиск с положительным ответом, иначе загружаем следующую вершину, и так до тех пор, пока либо найдём искомый элемент, либо не окажется следующей вершины (пришли в лист В-дерева).
Посмотрим на примере, как это реализуется.
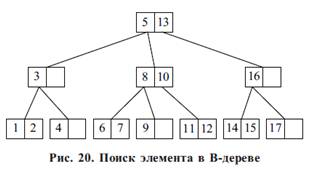
Будем искать элемент 11. Сначала загрузим корневую вершину. Эта вершина содержит элементы 5 и 13. Искомый элемент больше 5, но меньше 13. Значит, следует идти по ссылке, идущей от элемента 5. Загружаем следующую вершину (с элементами 8 и 10). Эта вершина тоже не содержит искомого элемента. Замечаем, что 11 больше 10, следовательно, двигаемся по ссылке, идущей от элемента 10. Загружаем соответствующую вершину (с элементами 11 и 12), в которой и находим искомый элемент. Итак, в этом примере, чтобы найти элемент, потребовалось три раза обратиться к внешней памяти для чтения очередной вершины.

20. NP-сложные и труднорешаемые задачи

Для оценки сложности алгоритма (см. введение) используется 0- символика.
На основе этой оценки можно привести следующую классификацию алгоритмов, при размере входных данных, равном n:
постоянные - сложность не зависит от и: 0(1);
линейные - сложность 0(n);
полиномиальные - сложность O(n~), где т - константа;
экспоненциальные - сложность 0(tt1">), где t - константа, которая больше 1, аул) - полиномиальная функция;
суперполиномиальные - сложность 0(Ф"1), где с - константа, à j(n)- функция возрастающая быстрее постоянной, но медленнее линейной;
Простые задачи (решаемые) - это задачи, решаемые за полиномиальное время.
Труднорешаемые задачи - это задачи, которые не решаются за полиномиальное время, либо алгоритм решения за полиномиальное время не найден.
Помимо этого, как было доказано А. Тьюрингом, существуют принципиально неразрешимые задачи.
Сложность задач не определяется по сложности наилучшего алгоритма, ее решающего. Для ценки сложности вводится классификация по сложности функций, вычисление которых возможно при задаваемых ограничениях на потребляемые ресурсы:
1) класс P - класс задач, которые можно решить за полиномиальное время;
2) класс NP - класс задач, которые можно решить за полиномиальное время только на недетерминированной Машине Тьюринга, которая в отличие от обычной Машины Тьюринга может делать предположения.Это задачи, у которых есть ответ, найти который трудно, но проверить можно за полиномиальное время;
3) класс NP-полных задач - класс задач, не менее сложных, чем любая NP-задача;
4) класс ЕХРТ1МЕ - класс задач, которые решаются за экспоненциальное время;
5) класс ЕХРТ1МЕ-полных задач - класс задач, которые не решаются за детерминированное полиномиальное время. Известно, что P <~ ЕХРПМЕ.
Очевидно, что P входит в NP, но вот проверить, что (P w NP) или (P = NP) до сих пор не удалось.