Правила и приемы ПР в условиях риска и неопределенности.

Зоны риска:

1. Безрисковая (отрицательные потери) – выигрыш

2. Зона допустимого риска – потери в виде рассчётной прибыли

3. Зона критического риска – потери в виде вложенных средств

4. Зона катастрофического риска – потери в виде имущественных средств

Кривая риска (см.лекции) – показывает вероятность возможных потерь.

Механизм риск-менеджмента

1. Процесс выработки рисковых альтернатив

2. Определение вероятности наступления события

3. Выявление степени и величины риска

4. Анализ окружающей обстановки

5. Выбор стратегии управления риском

6. Выбор приёмов управления риском и способов его снижения

7. Целенаправленное воздействие на риск

Методы оценки и снижения риска

Экономический, математико-статистический(страховые компании), экспертный, комбинированный (рейтинг) – сочетание эк. анализа и экспертных оценок.

Правила риск-менеджмента:

1. Нельзя рисковать больше, чем может позволить собственный капитал

2. Надо думать о последствиях риска

3. Нельзя рисковать многим ради малого дохода

4. Нельзя думать, что существует только одно решение

5. Положительные решения принимаются лишь при отсутствии сомнения

Приемы риск-менеджмента включают средства разрешения риска и приемы снижения его степени.

Крд <= 30%, Кр = Потери (имущество+затраты на восстановление)/Собств.Капитал

30%<=Ккр<=70%

Средства разрешения рисков:

1. Избежание рисков, уклонение от мероприятий, связанных с риском

2. Удержание риска - оставление риска за ЛПР, с пониманием того, что есть возможность минимизировать возможные потери за свой счет

3. Передача риска – передача ответственности за риск другому лицу (страхование)

Снижение риска: диверсификация, покупка дополнительной информации, лимитирование, самострахование, создание резервного фондов (обоснование допустимой величины резервного фонда, оценка упущенной выгоды от отвлечения Об. Средств), страхование и хеджирование, распределение между участниками, создание совместных предприятий, организация венчурных фирм.

Таблица решений, дерево решений. Сетевые методы разработки УР.

Теория игр

Применение теории игр в практике управления.Теория игр - инструмент, помогающий повысить эффективность плановых и управленческих решений.

Это раздел математики для изучения конфликтных ситуаций. Это значит, что можно выработать оптимальные правила поведения каждой стороны, участвующей в решении конфликтной ситуации.

Основные понятия теории игр. Втеории используются следующие понятия:

- игра — упрощенная формализованная модель реальной конфликтной ситуации. Математически формализация означает, что выработаны определенные правила действия сторон в процессе игры: варианты действия сторон; исход игры приданном варианте действия; объем информации каждой стороны о поведении всех других сторон.

- игрок — одна из сторон в игровой ситуации;

- стратегия игрока — правила действия игрока в каждой из возможных ситуаций игры. Существуют игровые системы управления — системы, процесс управления в которых рассматривается как игра;

- платежная матрица — матрица эффективности, матрица игры. Она включает все значения выигрышей (в конечной игре).

Платежная матрица

	Игрок 2
Игрок 1		B1	B2	…	Bn	αi
A1	a11	a12	…	a1n	Α1
А2	a21	a22	…	a1n	α2
…	…	…	…	…	…
Am	am1	am1	…	amn	αm
βj	β1	β2	…	βn

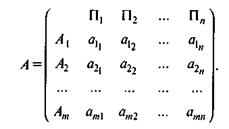Рассмотрим организацию и аналитическое представление игры с природой. Пусть игрок 1 имеет/и возможных стратегий: А₁,А₂, ...,А_т, а у природы имеется п возможных состояний (стратегий): П,, П₂, ..., П_л, тогда условия игры с природой задаются матрицей А выигрышей игрока 1:

Платит, не природа, а некая третья сторона (или совокупность сторон, влияющих на принятие решений игроком 1 и объединенных в понятие «природа»).

Возможен и другой способ задания матрицы игры с природой — не в виде матрицы выигрышей, а в виде так называемой матрицы рисков R = ||r_ij||_mn , или матрицы упущенных возможностей. Величина риска — это размер платы за отсутствие информации о состоянии среды. Матрица R может быть построена непосредственно из условий задачи или на основе матрицы выигрышей А.

Например, для матрицы выигрышей:

β₁= 4, β₂= 8, β₃= 6, β₄= 9.

Согласно введенным определениям r_ij и β_j. получаем матрицу рисков:

Для определения наилучших решений используются следующие критерии: максимакса, Вальда, Сэвиджа, Гурвица.

Выбор стратегии по критерию максимакса.С помощью этого критерия определяется стратегия, максимизирующая максимальные выигрыши для каждого состояния природы. Это критерий крайнего оптимизма. Наилучшим признается решение, при котором достигается максимальный выигрыш (М):

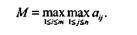
Нетрудно увидеть, что для матрицы А наилучшим решением будет А_{, при котором достигается максимальный выигрыш — 9.

Следует отметить, что ситуации, требующие применения такого критерия, в экономике в общем нередки, и пользуются им не только безоглядные оптимисты, но и игроки, поставленные в безвыходное положение, когда они вынуждены руководствоваться принципом «или пан, или пропал».

Выбор решения по критерию Вальда (максиминный критерий).С позиций данного критерия природа рассматривается как агрессивно настроенный и сознательно действующий противник. Выбирается решение, для которого достигается значение максимального критерия (W):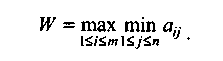

В соответствии с критерием Вальда из всех самых неудачных результатов выбирается лучший (W= 3). Это перестраховочная позиция крайнего пессимизма, рассчитанная на худший случай. Такая стратегия приемлема, например, в случаях, когда игрок не столь заинтересован в крупной удаче, но хочет себя застраховать от неожиданных проигрышей. Выбор такой стратегии определяется отношением игрока к риску.

Выбор решения по критерию Сэвиджа (минимаксный критерий).Выбор стратегии аналогичен выбору стратегии по принципу Вальда с тем отличием, что игрок руководствуется не матрицей выигрышей A, а матрицей рисков R: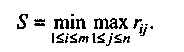

Выбор решения по критерию Гурвица (критерий пессимизма-оптимизма).Этот критерий при выборе решения рекомендует руководствоваться некоторым средним результатом, характеризующим состояние между крайним пессимизмом и безудержным оптимизмом. Согласно этому критерию стратегия в матрице А выбирается в соответствии со значением:

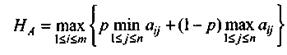
где Н_А — критерий пессимизма-оптимизма применительно к матрице А;

р — коэффициент пессимизма (0<р<1).

Дерево решений используется, если имеют место два или более последовательных множества решений (причем последующие решения основываются на результатах предыдущих) и/или два или более множества состояний среды (т.е. появляется целая цепочка решений, вытекающих одно из другого, которые соответствуют событиям, происходящим с некоторой вероятностью).

Дерево решений— это графическое изображение последовательности' решений и состояний среды с указанием соответствующих вероятностей и выигрышей для любых комбинаций альтернатив и состояний среды.

Процесс принятия решений с помощью дерева решений в общем случае предполагает выполнение следующих пяти этапов.

1. Формулирование задачи. Прежде всего, необходимо отбросить не относящиеся к проблеме факторы, а среди множества оставшихся выделить существенные и несущественные. Это позволит привести описание задачи принятия решения к поддающейся анализу форме.

2. Построение дерева решений.

3. Оценка вероятностей состояний среды, т.е. сопоставление шансов возникновения каждого конкретного события. Следует отметить, что указанные вероятности определяются либо на основании имеющейся статистики, либо экспертным путем.

4. Установление выигрышей (или проигрышей, как выигрышей со знаком минус) для каждой возможной комбинации альтернатив (действий) и состояний среды.

5. Решение задачи.

Правила построения дерева решений:

1. строится слева-направо

2. начинается с первого решения и его альтернативы

3. на события ЛПР влиять не может, поэтому носит вероятностный характер (вер.=1)

4. Заполнение дерева осуществляется справа-налево, начиная с МАХ дохода на каждой ветви

5. Для дальнейшего анализа выбирается решение, имеющее МАХ вероятный доход

6. Ветвь с меньшими доходами заёркивается