Формирование конкретной системы данных

Задачи линейного программирования

Конкретная система представляет собой таблицу числовых данных. В табл. 3.2 приведена транспортная таблица для задачи линейного программирования на примере конкретного описания системы данных J_k.

Таблица 3.2

Система данных

Инвестиционные проекты

Запасы

B1

B2

B3

B4

B5

B6

Ai

Активы

A1

A2

A3

31

A4

34

Заявки

bj

Остановимся на процедуре формирования конкретной матрицы чисел I_K в учебной системе, реализуемой, например, в виде алгоритма адресного наложения маски на таблицу случайных чисел [4, с.122]:

1 2

3 4

5 6

S

A1

A2

A3

1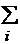

IK =

Б1

Б2

Б3

Þ 2

В1

В2

В3

3

Г1

Г2

Г3

4

0

+ 1

Маска М

Маска М

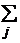aij

+ 1

S S

Вместо «0» в ячейку (46) добавляется значащая цифра оценки эффективности, например, 1.

Получим выборку по маске (при замене нуля на единицу) путем адресного наложения маски на поле случайных чисел. Представим результат в виде системы блочных матриц:

Aj

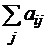A=[aij]

+ 1

Ai

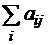+ 1

S S

Рассмотрев пример, можно приступить к описанию учебной системы объекта I_C , свойства которого позволят конструировать множество непересекающихся или частично непересекающихся наборов вариантов выборок для индивидуальных заданий по таблице случайных чисел, что важно для потока обучаемых в условиях ВУЗа. Маска выборок для I_K представляет собой часть адресной системы фрагмента таблицы двухразрядных случайных чисел размерности 20х20 с общим числом чисел 400:

		n	n + 1	n + 2
	m	r1	r2	r3
Маска	m + 1	r4	r5	r6	= M .
	m + 2	r7	r8	r9
	m + 3	r10	r11	r12

Алгоритм выборки. Маска М, описанная в системе собственных координат упорядоченным числом {r_ij}, своей ячейкой r₁ накладывается на ячейку таблицы случайных чисел. Для преодоления краевого эффекта используется правило вычетов по модулю m = 20, причем m Î N₂₀ = { А, Б, В, …, Ф}, т.е. от А и до Ф, где |{А;…Ф}|=20.

Например, для строки номер 21: 21 = 21 mod 20 = 1;

для строки номер 22: 22 = 22 mod 20 = 2.

т.е. n = n mod 20; m = m mod 20.

.

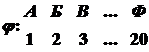Здесь m Î N₂₀ = {1, 2, …, 20} — числа перенумерованного алфавита по полной системе соответствий:

А		Е		Л		Р
Б		Ж		М		С
В		З		Н		Т
Г		И		О		У
Д		К		П		Ф

Система вычетов по модулю 20 позволяет замкнуть таблицу из 20 ´ 20 = 400 случайных чисел и сформировать 400 вариантов заданий при первом проходе таблицы случайных чисел, отличающихся адресно хотя бы в одном столбце своих наборов чисел в выборках по маскам. При этом наложение маски базируется по адресу числа r₁, т.е. задается начало выборки с любого адреса (m, n):

| { (m, n) } | = | { (A, 1); … ; (A, 20); (Б, 1); … ; (Б, 20); … … ; (Ф, 1); … ; (Ф, 20) } | = 400.

Другими словами, один проход таблицы с выборкой по маске М позволяет получить порядка 400 вариантов индивидуальных заданий, отличающихся в одном столбцовом наборе чисел.