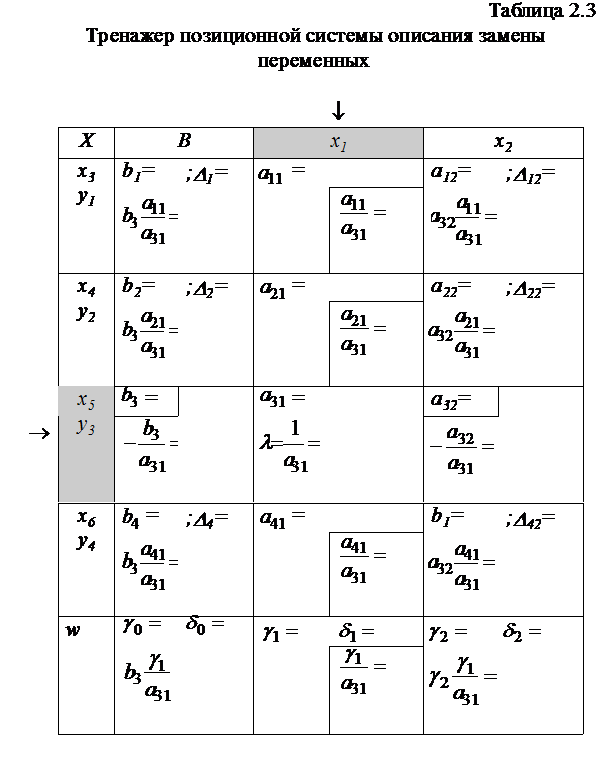
Система правил замены переменных

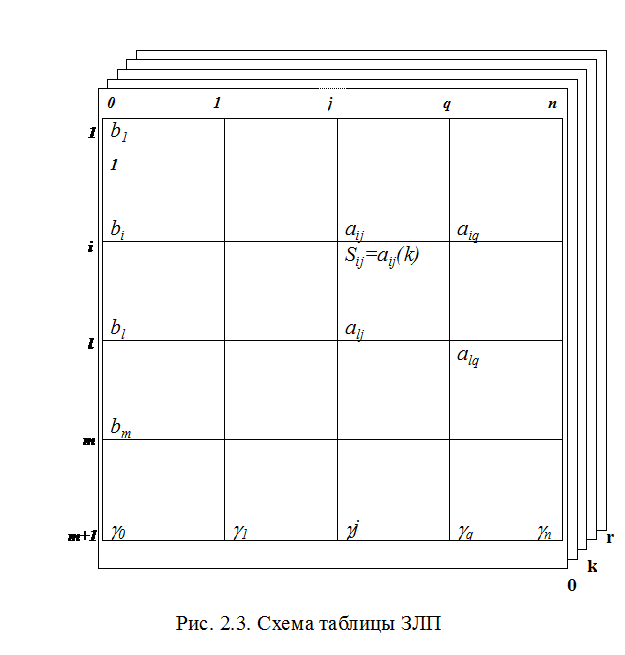
Построение системы правил на базе знаково-лингвистических представлений табличного варианта замены переменных приведено на рис. 2.3.

На рис. 2.3 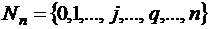– множество x_j, включая x₀=1 для свободных членов уравнений; 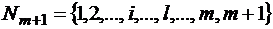– множество уравнений, включая

критерий эффективности (уравнение (m+1)); 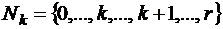– множество таблиц замены переменных, необходимое для поиска оптимального решения, где k – номер итерационного процесса kÎ{0,…,r}, k=0 – начальная таблица; Sij(k) := a_ij(k) – оператор присвоения адресу Sij(k) на шаге k значения a_ij(k)=T({a_ij(k-1)}).

Оператор T({a_ij(k-1)}) представляет описание правил деятельности по формированию таблицы для шага k.

Правила замены переменных представим для случая замены базовой переменной на свободную переменную x_q при переходе от k к k+1, т.е. [x_l(k)®x_q(k+1)]Ú[x_q(k) ®x_l(k+1)]:

1. x_l(k+1)=x_q(k); x_q(k+1)=x_l(k); остальные переменные не меняют своего места в таблице преобразований.

2. 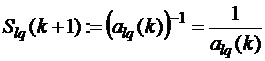– ячейка разрешающего элемента.

3. {S_lj(k+1)|j¹q} := {– 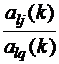} – элементы разрешающей строки.

4. {S_iq(k+1)|i¹l} := { 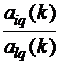} – элементы разрешающего столбца.

5. {S_ij(k+1)| (i¹l)Ù(i¹l)}:={a_ij(k)+ 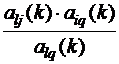} – все оставшиеся элементы таблицы.

Далее следует анализ полученного решения на оптимальность с выходом на окончание процесса замены переменных или его продолжение.

Инвестиционные проекты в концепции

Транспортной задачи ЛП

Транспортная топология инвестиций

Формирование заданий

В задаче об инвестировании работ в строительстве (см. задачу «Бетон», п.1) существенным фактором является возможность перенесения методов ее решения на абстрактном уровне на множество других задач. В частности, при ограниченном числе инвестиционных проектов и источников финансирования ориентировочные расчеты, выполняемые в форме транспортных таблиц, могут быть хорошим средством быстрого моделирования и сравнительной оценки основного ряда возможных альтернатив для выбора решений. Данный подход подтверждает и одновременно использует свойство изоморфизма моделей по отношению к различным предметным областям решаемых задач.

Пусть система определяется основной задачей нахождения оптимального размещения имеющихся активов.

,

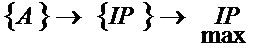где A – активы банка;

IP – возможные инвестиционные проекты;

IP_max – оптимальный инвестиционный проект.

С позиции топологического подхода, каждой схеме вложений можно сопоставить стоимостную меру полезности проекта. Следовательно, можно перейти к табличной форме представления (табл. 3.1.). На рис. 3.1 {A_i} – источники финансирования с активами a_ij ; {IP_j}– инвестиционные проекты; [a_ij] – удельная эффективность оценки капиталовложений из А_i в проект IP_j; {b_j}– сумма вложений по запросу заемщика на весь проект.

В реальной банковской системе при формировании системы данных для анализа прибыльности-ликвидности используется банковский отдел аналитики. Удельная эффективность капиталовложений в инвестиционные проекты формируется как результат анализа сведений, получаемых от различных информационных агентств, анализа экономических отчетов и обзоров, получаемых путем экспертных оценок и т. д.

Для учебных целей систему удельных данных по [a_ij] будем формировать, используя таблицу случайных чисел с равновероятным законом распределения [4, с. 122].

В дальнейшем используется система понятий системологии Клира для эмпирических систем [5], а именно: I_C – система объекта; I_K – конкретная система; I_A – общая или абстрактная система; комплекс < I_C ; I_K ; I_A > – исходная система; Д– система данных; F– система порождения и др.

Таблица 3.1

Стоимость инвестиционных проектов

	Инвестиционные проекты вложений (IP)	Активы
IP1			IPj		IPm	ai
Активы банка, подлежащие инвестированию из источников А0	A1	a11			a1j		a1m	a1
Ai	ai1			aij		aim	Ai
An	an1			anj		anm	an
Спрос	bj	b1			bj		bm

Упорядочиванием полученных в результате анализа данных, т.е. конкретизацией системы данных (D) исходной задачи субъекта, занимается отдел аналитики, формируя изначально систему

объекта – банка I_C. Из собранных данных формируется необходимая таблица данных. В результате получается структурированный массив данных. Система объекта I_C для учебных целей определяется заданием правил выборки подмножества чисел из таблицы случайных чисел. В итоге конструируется индивидуальный вариант задания обучаемого для практических занятий.

Для задачи размерности 4х6 абстрактная система удельной эффективности J_A имеет вид матрицы соответствующей размерности с элементами { a_ij}.