Последовательном исключении неизвестных из уравнений
2. Сведении матрицы коэффициентов к треугольному виду
3. Вычислении определителя, составленного из коэффициентов уравнения
4.(3)
Решение системы линейных уравнений методом Жордана состоит в:
Последовательном исключении неизвестных из уравнений
2. Сведении матрицы коэффициентов к диагональному виду
3. Вычислении определителя, составленного из коэффициентов уравнения
5.(4)
Сведение матрицы коэффициентов к диагональному виду
- суть метода решения систем линейных уравнений методом
_________________
6(5)
Сведение матрицы коэффициентов к треугольному виду
- суть метода решения систем линейных уравнений методом
__________.
7. (5)
При решении систем линейных уравнений методами Гаусса-Зейделя и простых итераций быстрее сходится к решению метод
___________
8.(5)
Решение систем линейных уравнений прямым методом Гаусса сводится к приведению матрицы коэффициентов к _____________
9.(5).
Решение систем линейных уравнений прямым методом Жордана сводится к приведению матрицы коэффициентов к _________________
10.(5).
Из прямых методов решения систем линейных уравнений обратный ход имеет метод ________.
11.(4)
Привести в соответствие:
слева
1. Решение систем линейных уравнений прямым методом Гаусса сводится к тому, что матрица коэффициентов имеет вид
2. Решение систем линейных уравнений прямым методом Жордана сводится к тому, что матрица коэффициентов имеет вид
справа
а) треугольный
б) диагональный
12.(4)
При решении систем линейных уравнений методом простых итераций, необходимо проверить условие:_(записать)
13.(3)
При решении систем линейных уравнений процесс итераций сходится к единственному решению, независимо от выбора начального приближения, если выполняется условие:____________.
14. (4)
Достаточное условие сходимости решения системы линейных уравнений можно проверить по формуле:_____________
15.(4)
Решение системы линейных уравнений методом Гаусса-Зейделя состоит из этапов (Указать последовательность):
1. Приведение системы к виду, в котором элементы главной диагонали превосходили бы остальные элементы строк
2. Проверка достаточного условия сходимости
3. Вычисление неизвестных , при котором предыдущие вычисленные значения неизвестных используются в последующих
4. Сравнение результатов с заданной точностью.
16(3).
Функциональная зависимость между У и Х ,полученная в результате экспериментальных данных называется:
Эмпирической
Аппроксимирующей функцией
3. Теоретической кривой
17 (3).
Для получения коэффициентов уравнения сглаживающей кривой обычно используется метод:
Наименьших квадратов
Гаусса
3. неопределенных коэффициентов
18.(3).
При нахождении коэффициентов уравнения сглаживающей кривой, имеющей вид нелинейного уравнения, необходимо привести его к линейному виду путем:
Замены переменных
2. Алгебраического преобразования
3. Разложения в ряд Тейлора
19.(3).
Показателем адекватности выбора аналитической зависимости, отражающей эмпирические данные, коэффициенты которой получены с использованием метода наименьших квадратов, является:
1. Стандартизированная ошибка аппроксимации:
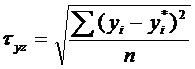 |
2. Погрешность, вычисленная на основе ошибки измерения исходных данных
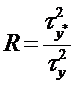 |
3. Индекс детерминации
20.(5)
Наиболее часто используемые нелинейные зависимости для описания эмпирических данных можно записать, используя обозначения неизвестной х и коэффициентов а, в так:
Степенная - y=
Экспонента- y=
Показательная- y=
Правую часть записывает студент
21.(5)
Наиболее часто используемые нелинейные зависимости для описания эмпирических данных через коэффициенты а,в можно записать так:
Гиперболическая – у=
Степенная – у=
Обратная - у=
Правую часть уравнения записывает студент
22.(5).
Наиболее часто используемые нелинейные зависимости для описания эмпирических данных через коэффициенты а, в можно записать так:
Дробно-линейная – у=
Логарифмическая - у=
Правую часть уравнения записывает студент
23.(4)
Наиболее часто используемые нелинейные зависимости для описания эмпирических данных
Привести в соответствие:
1.Степенная - а) y=bax -
2. Экспонента- б) y=beax
3. Показательная- - и) y=bxa
24.(4)
Наиболее часто используемые нелинейные зависимости для описания эмпирических данных
Привести в соответствие
1. Гиперболическая – а) у=в+а/х
2. Степенная – б) у=вха
3. Обратная - в) у=1/(ах+в)
25.(4)
Наиболее часто используемые нелинейные зависимости для описания эмпирических данных
Привести в соответствие
1. Степенная - а) y= beax
2. Экспонента- б) y= bxa
3. Показательная- в) y=bax
26.(4)
Наиболее часто используемые нелинейные зависимости для описания эмпирических данных
Привести в соответствие:
1. Гиперболическая – а) у=в+а/х
3. Обратная - в) у=1/(ах+в)
4. Дробно-линейная – г) у= х/(вх+а)
27.(5)
Привести в соответствие:
Слева.
1.Подбор приближенной похожей функции – это
2. Если функция проходит через узлы интерполяции, то эо
3.Найти значение функции в точке, принадлежащей области задания функции, но не совпадающей ни с одним узлом интерполяции, это
Справа:
1. Постановка задачи интерполяции
2. Аппроксимация
3. Интерполяци
28.(4)
Для нахождения неизвестных параметров по методу наименьших квадратов функцию надо привести к _______________виду.
29.(5)
Для нахождения неизвестных параметров «а» и «в» по методу наименьших квадратов функцию надо привести к линейному виду, сделав ________________ преобразования и _____________________
30.(5)
Сколько дробей будет в интерполяционном многочлене Лагранжа, если он проходит через 5 точек.
31.(5)
По сколько скобок в числителе и знаменателе будет в записи интерполяционного многочлена Лагранжа, если он записан для 5 точек
32.(5)
Можно ли получить уравнение прямой, проходящей через 2 точки, пользуясь формулой интерполяционного многочлена Лагранжа.
33.(5).
Сколько точек (минимально) необходимо взять для решения задачи квадратичной интерполяции
34 .(4)
Показателем адекватности выбора аналитической зависимости, отражающей эмпирические данные, коэффициенты которой получены с использованием метода наименьших квадратов является
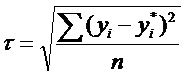 |
Стандартизированная _____________ аппроксимации:
35(3).
Теорема о существовании определенного интеграла формулируется так:
1. Если функция F(x) определена и непрерывна на (а,в), то предел интегральной суммы существует и не зависит ни от способа разбиения отрезка (а,в) на элементарные отрезки, ни от выбора точки
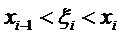
2. Если функция F(x) кусочно непрерывна на (а, в), то предел интегральной суммы существует и не зависит ни от способа разбиения отрезка (а, в) на элементарные отрезки, ни от выбора точки
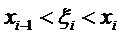 |
3. Если функция F(x) определена и непрерывна на (а, в), то предел интегральной суммы существует и зависит от способа разбиения отрезка (а, в) на элементарные отрезки, и не зависит от выбора точки
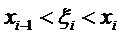 |
36.(3).
Приближенно вычислить интеграл можно представив подинтегральную функцию в виде: 1,2,3:
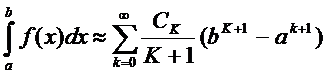 |
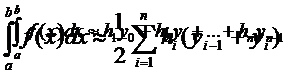 |

37.(3)
Приближенно вычислить интеграл можно воспользовавшись формулой прямоугольников (1,2,3)
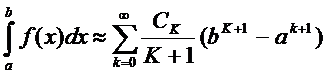 |
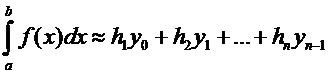
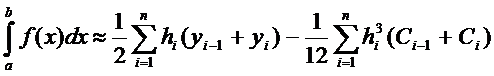
38.(3)
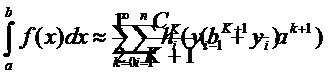 |
Вычислить интеграл можно воспользовавшись формулой трапеции.
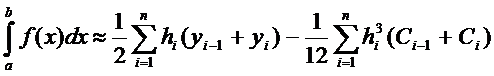 |
39.(3)
Приближенно вычислить интеграл можно воспользовавшись формулой Симпсона:
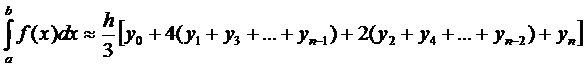
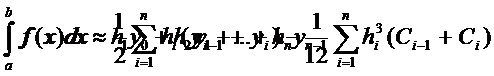 |
40.(3)
Какие из этих формул не являются формулами для вычисления интеграла трапеций
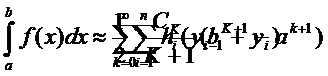 |
41.(4)
Привести в соответствие:
Приближенно вычислить интеграл можно представив подынтегральную функцию в виде:
Слева:
1.Площадей прямоугольников
2. Площадей трапеций
3. Площадей парабол
Справа: а,б,в
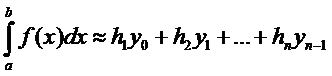 |
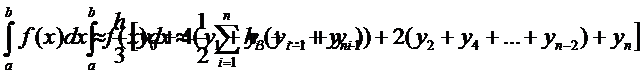
42.(3)
Результат приближенного вычисления интеграла по формуле трапеций можно оценить, вычислив остаточный член по формуле: (1,2,3)
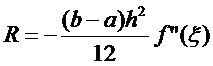
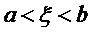
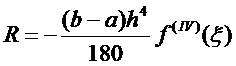
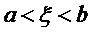
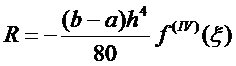
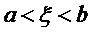
43.(3)
Результат приближенного вычисления интеграла по формуле Симпсона можно оценить, вычислив остаточный член по формулеL1,2,3)
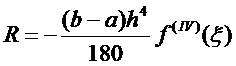
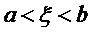
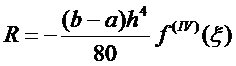
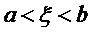
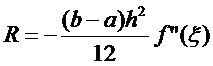
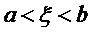
44.(3)
Привести в соответствие:
Результаты приближенных вычислений интеграла можно оценить для всех формул:
Слева:
1. Трапеций
2. Симпсона
3. Ньютона
Справа (а,б,в)
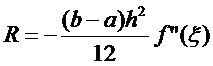
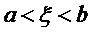
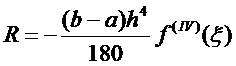
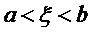
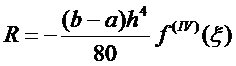
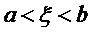
45(3)
Планирование эксперимента – это: (выбрать один ответ )
1. процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью.
2. стремление к минимизации числа опытов.
46(3)
Модель "черного ящика " предполагает:
1. Наличие входных и выходных параметров
2. Задание ограничений на входные параметры
3. Задание ограничений на выходные параметры
47(3)
Для проведения эксперимента необходима:
1. Возможность влияния на воздействие фактора
2. Способность алгоритма привести к расчету критериев значимости факторов
3. Возможность изменять условия во время проведения каждого опыта
48(3)
Уравнение, связывающее входные и выходной параметр, называется:
1. Функцией отклика
2. Интерполяционным многочленом
3. Квадратным трехчленом
49(3)
Каждый фактор может принимать при проведении опытов несколько значений, которые называются:
1. Средними
2. Уровнями
3. Значениями для построения линий одинакового выхода
50(3)
Параметром оптимизации может быть:
1. Любая функция, связывающая "вход" и "выход"
2. Функция, описывающая изменение поведения фактора во время проведения опыта
3. Функция, дающая наибольшее отклонение от ее среднего значения
51(4)
В матрице планирования эксперимента используются значения факторов:
1. Нормированные
2. Натуральные
3. Средние
52(3)
Оценка коэффициентов уравнения регрессии на значимость проводится по критерию
1. Фишера
2. Стьюдента
3. Чебышева
53(3)
Проверка уравнения на адекватность проводится по критерию:
1. Фишера
2 .Стьюдента
3 Чебышева
4. Гаусса
54.(3)
Алгоритм нахождения корня нелинейного уравнения итерационными методами состоит из: (выбрать)
1.Отыскания приближенного значения корня или содержащего его отрезка и уточнения до заданной степени точности.
2.Нахождения приближенного значения корня при начальных условиях, заданных системой неравенств
3.Получение области допустимых значений на основе решения системы уравнений
4.Вычисления производной и нахождения критической точки и уточнения до заданной точности
5.Нахождения суммы приращений
55.(4)
Отыскание приближенного значения корня или содержащего его отрезка и уточнение до заданной степени точности в этом суть алгоритма нахождения корня _____________ уравнения ___________________________ методами .
56.(4)
Если в процессе итерации в качестве приближений принимаются точки пересечения прямой, соединяющей две точки кривой на заданном отрезке с осью ОХ, то реализуется он с помощью метода (выбрать):
1.Бисекции
2.Ньютона
3.Простых итераций
4.Хорд
5.Лина
57. (4)
Если в процессе итерации в качестве приближений принимаются точки пересечения прямой, соединяющей две точки кривой на заданном отрезке с осью ОХ, то реализуется метод хорд
58.(3).
При решении нелинейного уравнения численными методами уравнение касательной используется в методе (выбрать):
1.Бисекции
2.Ньютона
3.Хорд
4.Простых итераций
5.Лина
59.(4)
Если при решении нелинейного уравнения численными методами используется уравнение прямой, имеющей одну общую точку с кривой, то реализуется
метод касательных (Ньютона)
60.(4).
При решении нелинейного уравнения численными методами принцип деления отрезка пополам используется в методе (выбрать):
1.Бисекции
2.Ньютона
3.Хорд
4.Простых итераций
5.Лина
61. (4)
Если при решении нелинейного уравнения численными методами, используется принцип деления отрезка пополам реализуется метод бисекции
62.(4)
Привести в соответствие:
Слева:
1.Если в процессе итерации в качестве приближений принимаются точки пересечения прямой, соединяющей две точки кривой на заданном отрезке с осью ОХ, то реализуется он с помощью метода:
2.При решении нелинейного уравнения численными методами уравнение касательной используется в методе:
3.При решении нелинейного уравнения численными методами принцип деления отрезка пополам используется в методе:
Справа:
1.Хорд
2.Ньютона
3.Бисекций
. 63.(3)
Если при отделении корня строим график функции и выбираем отрезок, включающий точку пересечения кривой с осью ОХ, то такой подход называется :________________ способом отделения корня.
64.(3)
Для отделения корня аналитически сначала необходимо функцию ___________________, а затем выбрать интервал, в котором функция меняет _____.
65.(5).
Первым этапом при решении нелинейного уравнения численными методами является
Отделение _______
66.(4)
Первым этапом при решении нелинейного уравнения численными методами является
__________ корня
67.(5)
При решении нелинейного уравнения численными методами используется принцип деления отрезка , в котором находится корень, пополам в методе
__________.
68.(5).
При решении нелинейного уравнения численными методами используется принцип, по которому проводится касательная к кривой в методе ________
69.(3)
Линейная интерполяция состоит в том, что:
