Задачи по теории вероятностей и математической
ЗАДАЧИ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ
СТАТИСТИКЕ
Теория вероятностей и математическая статистика
Глава 1. События и вероятность
Элементы комбинаторики
1.Сколькими способами может быть осуществлен выбор одного из объектов или 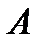 , или
, или 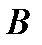 , если объект
, если объект 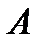 может быть выбран
может быть выбран 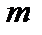 способами, а объект
способами, а объект 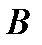 – другими
– другими 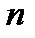 способами?
способами?
A) 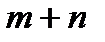 B)
B) 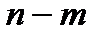 C)
C) 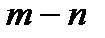 D)
D) 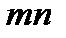 E)
E) 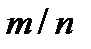
2. Сколькими способами может быть осуществлен выбор пары объектов A и B, если объект A может быть выбран 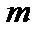 способами и после каждого из этих выборов объект
способами и после каждого из этих выборов объект 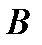 может быть выбран
может быть выбран 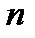 способами?
способами?
A) 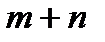 B)
B) 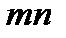 C)
C) 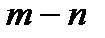 D)
D) 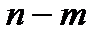 Е)
Е) 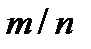
3.В ящике100микрокарт процессора. Известно, что 60 из них первого сорта, 25 – второго, а остальные третьего сорта. Сколько существует способов извлечения одной микрокарты первого или второго сорта?
A) 35 B) 75 C) 60 D) 40 E) 85
4. Сколькими способами из колоды карт можно выбрать или 1 валета, или 1 даму, или 1 короля?
A) 1 B) 4 C) 3 D) 12 E) 64
5. Сколькими способами из колоды карт можно выбрать 1 валета, 1 даму и 1 короля?
A) 12 B) 32 C) 64 D) 4 E) 3
6. Имеется 10 изделий 1-го сорта и 5 изделий 2-го сорта. Сколькими способами можно выбрать два изделия разных сортов?
A) 15 B) 50 C) 10 D) 5 E) 2
7.Вычислить 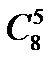 .
.
A) 14 B) 28 C) 56 D) 40 E) 112
8.Вычислить 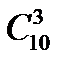 .
.
A) 120 B) 30 C) 60 D) 90 E) 240
9.Вычислить 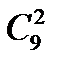 .
.
A) 144 B) 72 C) 18 D) 27 E) 36
10.Вычислить 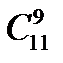 .
.
A) 33 B) 99 C) 11 D) 55 E) 110
11.Вычислить 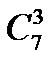 .
.
A) 42 B) 21 C) 35 D) 14 E) 70
12. Из ящика, содержащего 10 изделий первого сорта и 5 изделий второго сорта, наугад извлекают 2 изделия. В скольких случаях они окажутся одного сорта? 
A) 55 B) 50 C) 15 D) 105 E) 450
13. Из урны, содержащей 4 белых и 6 красных шаров, наугад вынимают 3 шара. В скольких случаях эти шары будут одного цвета?
A) 80 B) 12 C) 10 D) 24 E) 120
14. Для прохождения практики в банке на выделенные места претендуют 12 студентов, среди которых 5 отличников. Сколькими способами можно выбрать 8 студентов из этой группы так, чтобы среди них оказалось 3 отличника?
A) 10 B) 35 C) 31 D) 21 E) 210
15. Из 12 сбербанков 5 расположены за чертой города. Сколькими способами можно выбрать 5 сбербанков для аудиторской проверки так, чтобы 2 из них оказались за чертой города?
A) 210 B) 350 C) 45 D) 35 E) 31
Основные понятия и теоремы теории вероятностей
1.Чему равна вероятность достоверного события?
A) 0 B) 0,5 C) 0,9 D) 1 E) может быть любым числом
2. Чему равна вероятность невозможного события?
A) 0 B) 0,1 C) 0,5 D) 1 E) может быть любым числом
3. Какому условию удовлетворяет вероятность случайного события?
A) 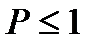 B)
B) 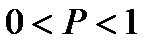 C)
C) 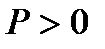 D)
D) 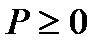 E)
E) 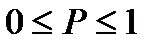
4. Вероятность события A равна р. Чему равна вероятность противоположного события?
A) 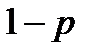 B)
B) 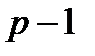 C)
C) 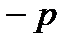 D) 0 E) 1
D) 0 E) 1
5.Если события A и B несовместны, то справедливо равенство:
A) 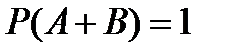 B)
B) 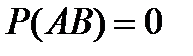 C)
C) 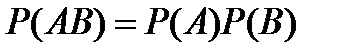
D) 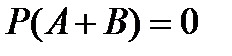 E)
E) 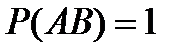
6.Событие A называют независимым от события B, если:
A) 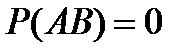 B)
B) 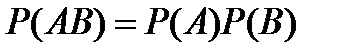 C)
C) 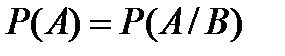
D) 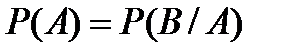 E)
E) 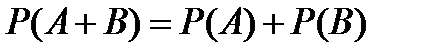
7.По какой формуле вычисляется вероятность совместного появления двух независимых событий?
A) 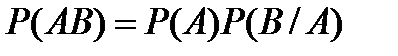 B)
B) 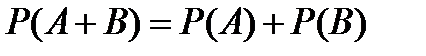 C)
C) 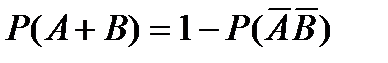
D) 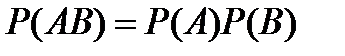 E)
E) 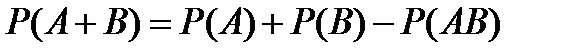
8.По какой формуле вычисляется вероятность совместного появления двух зависимых событий?
A) 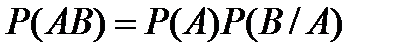 B)
B) 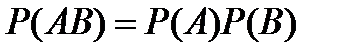 C)
C) 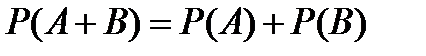
D) 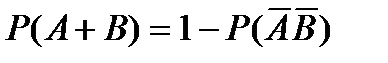 E)
E) 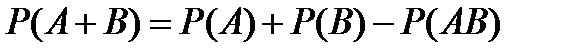
9.По какой формуле вычисляется вероятность появления хотя бы одного из двух независимых событий?
A) 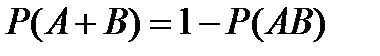 B)
B) 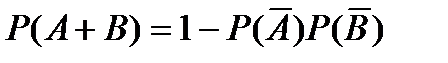 C)
C) 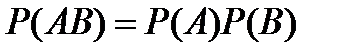
D) 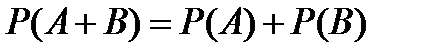 E)
E) 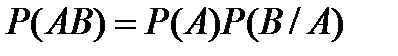
10.Чему равнавероятность события C – появления только одного из двух независимых событий A и B?
A) 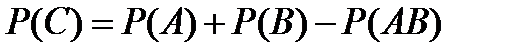 B)
B) 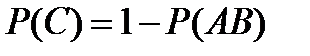 C)
C) 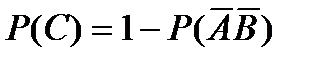
D) 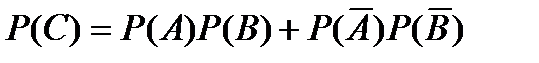 E)
E) 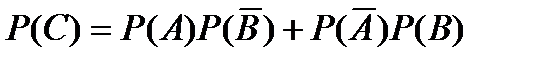
Теорема умножения
1.В урне 5 белых и 6 черных шаров. Наудачу вынимают два шара без возвращения. Пусть A− первый вынутый шар белый, B−второй вынутый шар белый. Найти P(B/A).
A) 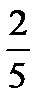 B)
B) 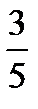 C)
C) 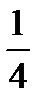 D)
D) 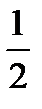 E)
E) 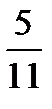
2.В ящике 7 стандартных и 3 нестандартных детали. Наудачу берут две детали без возвращения. Пусть A− первая деталь стандартная, B− вторая деталь стандартная. Найти P(B/A).
A) 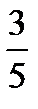 B)
B) 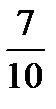 C)
C) 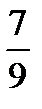 D)
D) 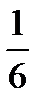 E)
E) 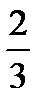
3.На книжной полке стоят 4 книги по экономике и 5 книг по истории. На удачу берут две книги без возвращения. Пусть A−первая книга по истории, B− вторая книга по истории. Найти P(B/A).
A) 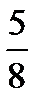 B)
B) 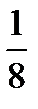 C)
C) 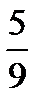 D)
D) 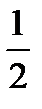 E)
E) 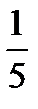
4.В ящике 10 стандартных и 6 нестандартных деталей. Наудачу берут две детали без возвращения. Пусть A−первая деталь стандартная, B− вторая деталь стандартная. Найти P(B/A).
A) 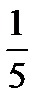 B)
B) 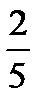 C)
C) 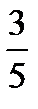 D)
D) 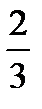 E)
E) 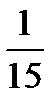
5.В урне 4 белых и 9 черных шаров. Наудачу вынимают два шара без возвращения. Пусть A−первый вынутый шар черный, B−второй вынутый шар черный. Найти P(B/A).
A) 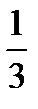 B)
B) 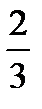 C)
C) 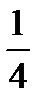 D)
D) 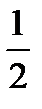 E)
E) 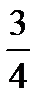
6.В коробке 4 простых и 6 цветных карандашей. Наугад вынимают два карандаша без возвращения. Пусть A−первый карандаш простой, B−второй карандаш простой. Найти P(B/A).
A) 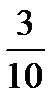 B)
B) 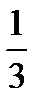 C)
C) 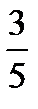 D)
D) 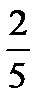 E)
E) 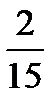
7.В пачке 7 тетрадей в клетку и 4 в линейку. Извлекают две тетради без возвращения. Пусть A− первая тетрадь в клетку , B− вторая тетрадь в клетку. Найти P(B/A).
A) 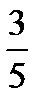 B)
B) 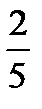 C)
C) 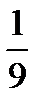 D)
D) 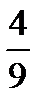 E)
E) 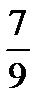
8.На полке стоят 6 книг по истории и 3 книги по географии. Наудачу берут две книги без возвращения. Пусть A−первая книга по географии, B− вторая книга по географии. Найти P(B/A).
A) 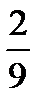 B)
B) 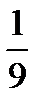 C)
C) 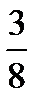 D)
D) 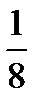 E)
E) 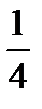
9.В группе 12 девушек и 9 юношей. По списку наугад вызывают двух студентов. Пусть A−первым вызван юноша, B− вторым вызван юноша. Найти P(B/A).
A) 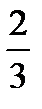 B)
B) 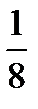 C)
C) 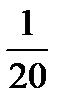 D)
D) 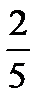 E)
E) 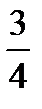
10.Студент не выучил 3 вопроса из 13. Преподаватель задает два вопроса. Пусть A− студент ответит на первый вопрос, B − студент ответит на второй вопрос. Найти P(B/A).
A) 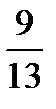 B)
B) 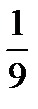 C)
C) 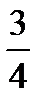 D)
D) 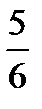 E)
E) 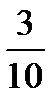
11.Студент пришел на зачет, выучив 7 вопросов из 15. Найти вероятность того, что он ответит на 2 заданных вопроса.
A) 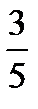 B)
B) 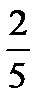 C)
C) 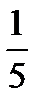 D)
D) 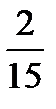 E)
E) 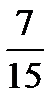
12.Из коробки, содержащей 4 красных и 6 зеленых карандашей, случайно выпали 2 карандаша. Найти вероятность того, что они оба красные.
A) 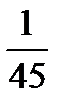 B)
B) 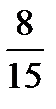 C)
C) 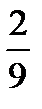 D)
D) 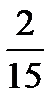 E)
E) 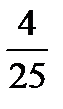
13.В ящике 4 стандартных и 2 нестандартных детали. Наудачу берут две детали. Найти вероятность того, что они обе стандартные.
A) 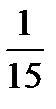 B)
B) 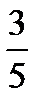 C)
C) 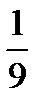 D)
D) 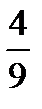 E)
E) 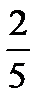
14.В урне 5 белых и 4 черных шара. Вынимают наугад два шара. Найти вероятность того, что они оба черные.
A) 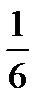 B)
B) 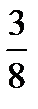 C)
C) 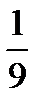 D)
D) 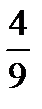 E)
E) 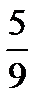
15.Из коробки, содержащей 4 красных и 6 зеленых карандашей, случайно выпали 2 карандаша. Найти вероятность того, что они оба зеленые.
A) 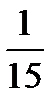 B)
B) 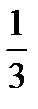 C)
C) 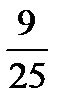 D)
D) 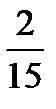 E)
E) 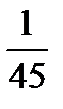
16.В ящике 4 стандартных и 3 нестандартных детали. Наудачу вынимают две детали. Найти вероятность того, что они обе нестандартные.
A) 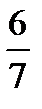 B)
B) 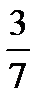 C)
C) 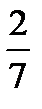 D)
D) 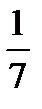 E)
E) 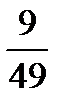
17.В группе 16 студентов, из них 9 юношей. Наугад выбирают двух студентов. Найти вероятность того, что выбраны юноши.
A) 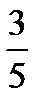 B)
B) 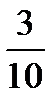 C)
C) 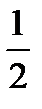 D) E)
D) E) 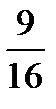
18.В урне 6 красных и 3 черных шара. Вынимают наугад два шара. Найти
вероятность того, что они оба красные.
A) 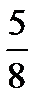 B) C)
B) C) 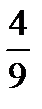 D)
D) 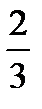 E)
E) 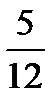
19. Среди 16 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что 2 наудачу выбранные билета окажутся выигрышными.
A) 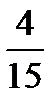 B)
B) 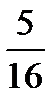 C)
C) 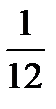 D)
D) 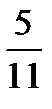 E)
E) 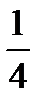
20.В ящике 10 деталей, среди которых 7 окрашенных. Сборщик наудачу извлекает две детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.
A) 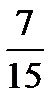 B) C)
B) C) 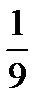 D)
D) 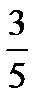 E)
E) 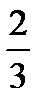
21.Устройство имеет два независимо работающих узла. Вероятности безотказной работы узлов равны соответственно 0,6 и 0,7. Найти вероятность безотказной работы двух узлов.
A) 1,3 B) 0,45 C) 0,46 D) 0,88 E) 0,42
22.Произведен залп двух орудий по цели. Вероятность попадания из первого орудия равна 0,8, из второго 0,7. Найти вероятность двух попаданий.
A) 0,62 B) 0,37 C) 0,56 D) 0,38 E) 1,5
23.Вероятности банкротства для двух однотипных предприятий соответственно равны 0,2 и 0,1. Найти вероятность банкротства обоих предприятий.
A) 0,72 B) 0,02 C) 0,3 D) 0,28 E) 0,26
24.В цехе установлены два сигнализатора, которые при аварии включаются с вероятностями 0,9 и 0,7. Найти вероятность того, что при аварии включатся оба сигнализатора.
A) 0,63 B) 0,03 C) 0,97 D) 0,34 E) 1,6
25.Два стрелка стреляют по мишени. Вероятности промаха соответственно равны 0,1 и 0,3. Найти вероятность того, что при одном залпе будет два промаха.
A) 0,34 B) 0,63 C) 0,3 D) 0,03 E) 0,4
26.В первом ящике 70% стандартных деталей, во втором 40%. Из каждого ящика вынули наугад по одной детали. Найти вероятность того, что обе детали стандартные.
A) 0,54 B) 0,28 C) 0,82 D) 0,46 E) 1,1
27.Вероятность повышения цены на молоко в текущем месяце равна 0,8, на муку – 0,6. Найти вероятность того, что в текущем месяце цена
повысится на оба товара.
A) 0,44 B) 0,4 C) 1,4 D) 0,92 E) 0,48
28.Два студента выполняют расчеты. Вероятности ошибки равны 0,3 и 0,2 соответственно. Найти вероятность того, что ошибку допустят оба студента.
A) 0,44 B) 0,5 C) 0,06 D) 0,38 E) 0,37
29.В первой урне 2 белых и 8 черных шаров, во второй – 3 белых и 2 черных шара. Из каждой урны вынули по одному шару. Найти вероятность того, что они оба белые.
A) 0,4 B) 0,8 C) 0,44 D) 0,12 E) 0,56
30.Рабочий обслуживает 2 станка. Вероятность того, что в течение часа станок остановится, равна 0,2 для первого станка, 0,25 − для второго. Найти вероятность того, что в течение часа остановятся оба станка.
A) 0,05 B) 0,5 C) 0,45 D) 0,6 E) 0,4
Теорема сложения
1. Какова вероятность того, что последняя цифра случайно выбранного телефонного номера равна 5 или 7?
A) 0,1 B) 0,2 C) 0,3 D) 0,4 E) 0,5
2. Вероятность того, что стрелок, произведя выстрел, выбьет 10 очков, равна 0,4, 9 очков – 0,3 и, наконец, 8 или меньше очков – 0,3. Найти вероятность того, что стрелок выбьет не менее 9 очков при одном выстреле.
A) 0,3 B) 0,4 C) 0,5 D) 0,6 E) 0,7
3. Данное предприятие производит 20% продукции высшего сорта и 70% продукции первого сорта, остальная продукция второго сорта. Найти вероятность того, что случайно взятое изделие окажется первого или второго сорта.
A) 0,5 B) 0,6 C) 0,7 D) 0,8 E) 0,9
4.Мастер обслуживает 4 станка. 20% рабочего времени он проводит у первого станка, 30 – у второго, 15 – у третьего, остальное время – у четвертого. Найти вероятность того, что в случайно выбранный момент времени он находится у третьего или четвертого станка.
A) 0,3 B) 0,45 C) 0,35 D) 0,5 E) 0,25
5.В ящике100микрокарт процессора. Известно, что 60 из них первого сорта, 25 – второго, а остальные третьего сорта. Найти вероятность того, что случайно взятая микрокарта окажется второго или третьего сорта.
A) 0,4 B) 0,35 C) 0,25 D) 0,75 E) 0,85
6.Устройство имеет два независимо работающих узла. Вероятности безотказной работы узлов равны соответственно 0,6 и 0,7. Найти вероятность безотказной работы только одного узла.
A) 0,46 B) 0,45 C) 0,42 D) 0,88 E)1,3
7.Произведен залп двух орудий по цели. Вероятность попадания из первого орудия равна 0,8, из второго 0,7. Найти вероятность только одного попадания.
A) 0,62 B) 0,37 C) 0,56 D) 0,38 E) 1,5
8.Вероятности банкротства для двух однотипных предприятий соответственно равны 0,2 и 0,1. Найти вероятность банкротства только одного предприятия.
A) 0,25 B) 0,26 C) 0,3 D) 0,02 E) 0,08
9.В первом ящике 70% стандартных деталей, во втором 40%. Из каждого ящика вынули наугад по одной детали. Найти вероятность того, что только
одна из них стандартная.
A) 1,1 B) 0,28 C) 0,82 D) 0,46 E) 0,54
10.В цехе установлены два сигнализатора, которые при аварии включаются с вероятностями 0,9 и 0,7. Найти вероятность включения при аварии только одного сигнализатора.
А) 0,97 B) 0,03 C) 0,34 D) 0,63 E) 1,6
11.Два стрелка стреляют по мишени. Вероятности промаха соответственно равны 0,1 и 0,3. Найти вероятность того, что при одном залпе промахнется только один стрелок.
A) 0,4 B) 0,66 C) 0,3 D) 0,03 E) 0,34
12.Вероятность повышения цены на молоко в текущем месяце равна 0,8,
на муку – 0,6. Найти вероятность того, что в текущем месяце цена повысится только на один товар.
A) 0,48 B) 0,4 C) 0,44 D) 0,92 E) 1,4
13.Два студента выполняют расчеты. Вероятности того, что они допустят ошибку, равны 0,3 и 0,2 соответственно. Найти вероятность того, что ошибку допустит только один студент.
A) 0,38 B) 0,5 C) 0,44 D) 0,06 E) 0,37
14.В первой урне 2 белых и 8 черных шаров, во второй – 3 белых и 2 черных шара. Из каждой урны вынули по одному шару. Найти вероятность того, что только один из них белый.
A) 0,8 B) 0,56 C) 0,44 D) 0,4 E) 0,12
15. Рабочий обслуживает 2 станка. Вероятность остановки равна 0,2 для первого станка, 0,25 − для второго. Найти вероятность того, что остановится только один станок.
A) 0,5 B) 0,05 C) 0,45 D) 0,35 E) 0,85
16.Вероятность изготовления бракованного изделия равна 0,1. Найти вероятность того, что из двух наудачу взятых изделий хотя бы одно окажется бракованным.
A) 0,01 B) 0,09 C) 0,18 D) 0,19 E) 0,99
17.Вероятность попадания в цель при одном выстреле равна 0,3. Найти вероятность хотя бы одного попадания при двух выстрелах.
A) 0,51 B) 0,21 C) 0,42 D) 0,09 E) 0,91
18. Вероятность изготовления изделия высшего сорта равна 0,7. Найти вероятность того, что из двух наудачу взятых изделий хотя бы одно окажется высшего сорта.
A) 0,1 B) 0,51 C) 0,42 D) 0,21 E) 0,91
19.Вероятность выигрыша в лотерею на один билет равна 0,2. Куплено два билета. Найти вероятность хотя бы одного выигрыша.
A) 0,32 B) 0,36 C) 0,96 D) 0,16 E) 0,04
20.Устройство содержит два независимо работающих узла. Вероятность безотказной работы узла равна 0,8. Найти вероятность безотказной работы хотя бы одного узла.
A) 0,16 B) 0,32 C) 0,96 D) 0,36 E) 0,64
21.Рабочий обслуживает 2 станка. Вероятность остановки равна 0,2 для первого станка, 0,25 − для второго. Найти вероятность того, что остановится хотя бы один станок.
A) 0,45 B) 0,6 C) 0,4 D) 0,05 E) 0,35
22.Вероятности банкротства для двух однотипных предприятий соответственно равны 0,2 и 0,1. Найти вероятность банкротства хотя бы одного предприятия.
A) 0,98 B) 0,3 C) 0,72 D) 0,8 E) 0,28
23.Вероятностиуспешной сдачи экзамена для двух студентов соответственно равны 0,7 и 0,8. Найти вероятность успешной сдачи экзамена хотя бы одним студентом.
A) 0,4 B) 0,94 C) 0,56 D) 0,44 E) 1,5
24.Два стрелка стреляют по мишени. Вероятности попадания соответственно равны 0,7 и 0,6. Найти вероятность хотя бы одного попадания при одном залпе.
A) 0,88 B) 0,58 C) 0,42 D) 1,3 E) 0,12
25.Завод получает необходимые детали с двух баз. Вероятность наличия нужных деталей на первой базе равна 0,8, на второй – 0,9. Найти вероятность того, что нужный материал окажется хотя бы на одной базе.
A) 0,72 B) 0,02 C) 0,28 D) 0,98 E) 1,7
Глава 2. Случайные величины
Случайных величин
1.Вероятность изготовления стандартной детали равна 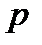 . Найти вероятность того, что из 4 проверенных деталей стандартными окажутся 3 детали.
. Найти вероятность того, что из 4 проверенных деталей стандартными окажутся 3 детали.
A) 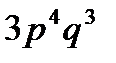 B)
B) 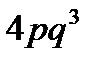 C)
C) 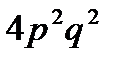 D)
D) 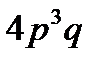 E)
E) 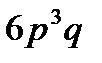
2.Вероятность того, что клиент банка вернет кредит, равна 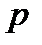 . Найти вероятность того, что из 5 случайно отобранных клиентов 3 вернут кредит.
. Найти вероятность того, что из 5 случайно отобранных клиентов 3 вернут кредит.
A) 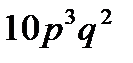 B)
B) 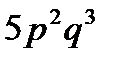 C)
C) 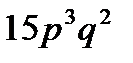 D)
D) 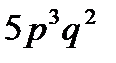 E)
E) 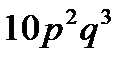
3.Некоторая фирма имеет сеть брокеров на бирже. Вероятность того, что брокер будет играть удачно, равна 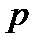 . Найти вероятность того, что из 6 брокеров 2 будут играть удачно.
. Найти вероятность того, что из 6 брокеров 2 будут играть удачно.
A) 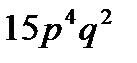 B)
B) 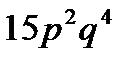 C)
C) 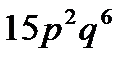 D)
D) 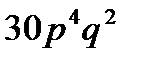 E)
E) 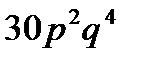
4. Вероятность того, что в цехе расход электроэнергии не превысит суточной нормы, равна 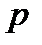 . Найти вероятность того, что за 7 дней расход электроэнергии не превысит суточной нормы в течение 4 дней.
. Найти вероятность того, что за 7 дней расход электроэнергии не превысит суточной нормы в течение 4 дней.
A) 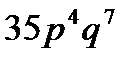 B)
B) 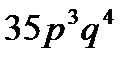 C)
C) 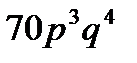 D)
D) 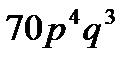 E)
E) 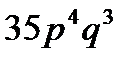
5. Каждое из 8 предприятий отрасли выполняет месячный план с вероятностью 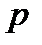 . Найти вероятность того, что в конце месяца выполнят план 6 предприятий.
. Найти вероятность того, что в конце месяца выполнят план 6 предприятий.
A) 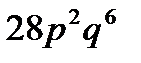 B)
B) 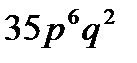 C)
C) 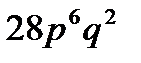 D)
D) 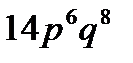 E)
E) 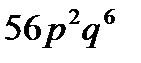
6.Вероятность банкротства к концу года для каждой из 6 фирм равна 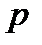 . Найти вероятность банкротства к концу года 3 фирм.
. Найти вероятность банкротства к концу года 3 фирм.
A) 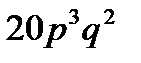 B)
B) 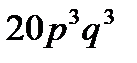 C)
C) 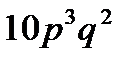 D)
D) 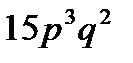 E)
E) 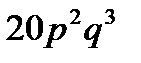
7.Вероятность появления ошибки при заполнении счета равна 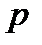 . Найти вероятность того, что из семи случайно отобранных счетов будут
. Найти вероятность того, что из семи случайно отобранных счетов будут
содержать ошибки 2 счета.
A) 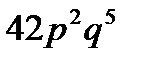 B)
B) 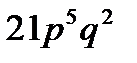 C)
C) 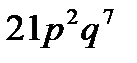 D)
D) 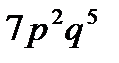 E)
E) 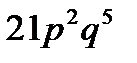
8. Вероятность того, что покупателю необходима обувь 41-го размера, равна 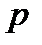 . Найти вероятность того, что из 8 покупателей обувь этого размера потребуют 3 покупателя.
. Найти вероятность того, что из 8 покупателей обувь этого размера потребуют 3 покупателя.
A) 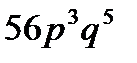 B)
B) 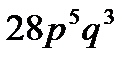 C)
C) 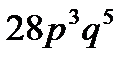 D)
D) 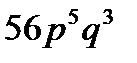 E)
E) 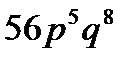
9. Вероятность продажи пакета акций на аукционе по первоначально заявленной цене равна 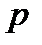 . Найти вероятность того, что из 9 пакетов акций по первоначально заявленной цене будут проданы 2 пакета.
. Найти вероятность того, что из 9 пакетов акций по первоначально заявленной цене будут проданы 2 пакета.
A) 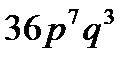 B)
B) 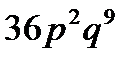 C)
C) 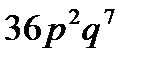 D)
D) 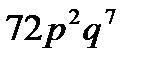 E)
E) 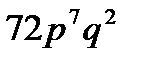
10. Вероятность того, что страховая компания будет выплачивать по договорам страховку, равна 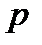 . Найти вероятность того, что по истечении срока 10 договоров компания уплатит страховку в 2 случаях.
. Найти вероятность того, что по истечении срока 10 договоров компания уплатит страховку в 2 случаях.
A) 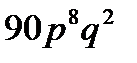 B)
B) 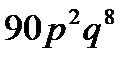 C)
C) 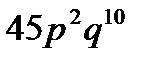 D)
D) 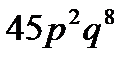 E)
E) 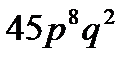
11. По какой формуле находят наивероятнейшее число появлений события?
A) 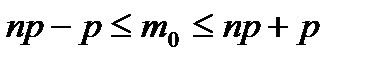 B)
B) 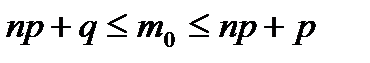 C)
C) 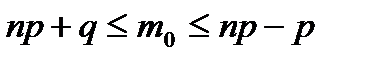
D) 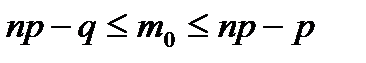 E)
E) 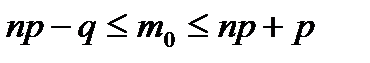
12.Найти наивероятнейшее число выпадений герба, если монету подбрасывают 14 раз.
A) 8 B) 6 C) 5 D) 7 E) 9
13.Найти наивероятнейшее число попаданий мячом в корзину при 11 бросках, если вероятность попадания при одном броске равна 0,8.
A) 9 B) 7 C) 8 D) 6 E) 10
14.Вероятность изготовления изделия высшего сорта равна 0,7. Найти наивероятнейшее число изделий высшего сорта среди 7 отобранных.
A) 6 B) 5 C) 4 D) 3 E) 2
15.Вероятность того, что студент правильно ответит на вопрос теста методом простого угадывания, равна 0,2. Найти наивероятнейшее число правильных ответов на 30 тестов.
A) 8 B) 7 C) 6 D) 9 E) 10
16.Вероятность попадания в цель при одном выстреле равно 0,9. Найти наивероятнейшее число попаданий в цель при 12 выстрелах.
A) 9 B) 10 C) 11 D) 8 E) 12
17.В цехе работает 7 станков. Вероятность остановки станка в течение часа равна 0,6. Найти наивероятнейшее число станков, остановившихся в течение часа.
A) 6 B) 5 C) 2 D) 3 E) 4
18.В магазин вошли 15 покупателей. Вероятность совершить покупку для каждого из них равна 0,3. Найти наивероятнейшее число покупателей, совершивших покупку.
A)4 B) 5 C) 6 D) 7 E) 8
19.Вероятность того, что прибор выдержит испытание, равна 0,9. Найти наивероятнейшее число приборов, выдержавших испытание, если испытывают 7 приборов.
A) 4 B) 6 C) 5 D) 7 E) 3
20.Вероятность заболевания гриппом во время эпидемии равна 0,4. Найти наивероятнейшее число заболевших из 6 сотрудников фирмы.
A) 1 B) 2 C) 3 D) 4 E) 5
21.Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0,8. Найти наивероятнейшее число элементов, которые выдержат испытание.
A) 12 B) 13 C) 14 D) 10 E) 11
22.Еслислучайная величина Х распределена по биномиальному закону, то ее математическое ожидание равно:
A) 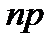 B)
B) 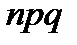 C)
C) 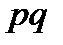 D)
D) 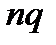 E)
E) 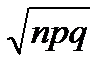
23.Еслислучайная величина Х распределена по биномиальному закону, то ее дисперсия равна:
A) 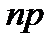 B)
B) 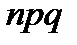 C)
C) 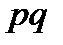 D)
D) 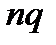 E)
E) 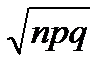
24.Две игральные кости подбрасывают 60 раз. Найти математическое ожидание числа испытаний, в которых сумма выпавших очков равна 4.
A) 12 B) 3 C) 4 D) 6 E) 5
25. Математическое ожидание числа отказов прибора в 10 независимых испытаниях равно 3. Вероятности отказа в каждом испытании одинаковы. Найти дисперсию числа отказавших приборов.
A) 21 B) 0,21 C) 2,1 D) 0,9 E) 1,8
26.Сколько раз нужно подбросить две монеты для того, чтобы математическое ожидание числа выпадений двух гербов было равно 12?
A) 12 B) 24 C) 16 D) 48 E) 8
27.Вероятность попадания при каждом выстреле равна 0,4. Сколько нужно сделать выстрелов, чтобы дисперсия числа попаданий в мишень была равна 6?
A) 40 B) 30 C) 35 D) 25 E) 45
28.Вероятность выигрыша в лотерею на один билет равна 0,2. Сколько нужно купить билетов, чтобы математическое ожидание числа выигрышей по ним было равно 10?
A) 25 B) 30 C) 35 D) 45 E) 50
29.Две монеты подбрасывают 16 раз. Найти дисперсию числа выпадений двух гербов.
A) 2 B) 3 C) 1 D) 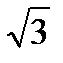 E) 4
E) 4
30.Сколько раз нужно подбросить игральную кость, чтобы дисперсия числа выпадений шести очков была равна 10?
A) 72 B) 66 C) 60 D) 36 E) 30
31.Вероятность изготовления стандартного изделия равна 0,8. Сколько нужно проверить изделий, чтобы дисперсия числа стандартных изделий среди проверенных была равна 4.
A) 15 B) 20 C) 25 D) 10 E) 30
32.Из урны, содержащей 2 белых и 6 черных шаров, извлекают один шар и возвращают обратно. Испытание повторяют 80 раз. Найти дисперсию числа испытаний, в которых появился белый шар.
A) 10 B) 15 C) 20 D) 12 E) 8
33.Математическое ожидание числа попаданий в цель при 30 выстрелах равно 18. Вероятность попадания от выстрела к выстрелу не меняется. Найти дисперсию числа попаданий.
A) 7,2 B) 10,8 C) 3,6 D) 0,24 E) 2,4
34. Если случайная величина X распределена по закону Пуассона, то вероятность появления события (X=m) определяется по формуле:
A) 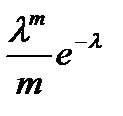 B)
B) 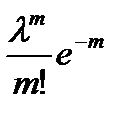 C)
C) 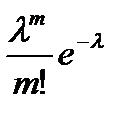 D)
D) 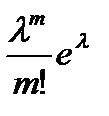 E)
E) 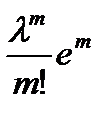
35.Какой закон распределения обладает свойством: «математическое ожидание равно дисперсии»?
A) Закон Пуассона B) Биномиальный C) Показательный
D) Нормальный E) Равномерный
36.Случайная величина Х распределена по закону Пуассона. Среднее квадратическое отклонение равно 5. Математическое ожидание равно:
A) 5 B) 25 C) 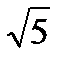 D)
D) 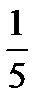 E)
E) 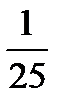
37.Случайная величина Х распределена по закону Пуассона. Математическое ожидание равно 9. Дисперсия Х равна:
A) 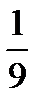 B)
B) 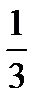 C) 81 D) 3 E) 9
C) 81 D) 3 E) 9
38.Случайная величина Х распределена по закону Пуассона. Математическое ожидание равно 4. Среднее квадратическое отклонение Х равно:
A) 16 B) 4 C) 8 D) 2 E) 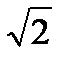
39.Случайная величина Х распределена по закону Пуассона. Дисперсия равна 16. Математическое ожидание Х равно:
A) 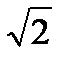 16 B) 2 C) 4 D) 8 E) 16
16 B) 2 C) 4 D) 8 E) 16
40.Случайная величина Х распределена по закону Пуассона. Среднее квадратическое отклонение равно 3. Математическое ожидание равно:
A) 81 B) 9 C) 3 D) 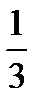 E)
E) 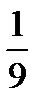
41.Учебник издан тиражом 20000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно три бракованных книги.
A) 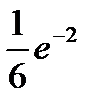 B)
B) 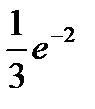 C)
C) 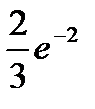 D)
D) 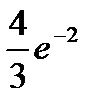 E)
E) 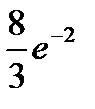
42.Вероятность того, что стодолларовая купюра фальшивая, равна 0,001. Найти вероятность того, что из 3000 купюр ровно три купюры окажутся фальшивыми.
A) 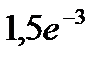 B)
B) 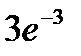 C)
C) 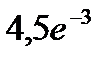 D)
D) 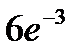 E)
E) 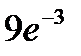
43.Вероятность выигрыша по одному лотерейному билету равна 0,01. Найти вероятность того, что из 400 лотерейных билетов ровно два окажутся выигрышными.
A) 8 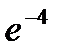 B) 6
B) 6 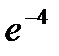 C) 4
C) 4 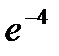 D) 2
D) 2 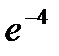 E)
E) 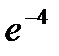
44.Месячное количество дождливых дней в определенном городе подчиняется закону Пуассона со средним значением, равным 6 дней. Найти вероятность того, что в следующем месяце будет три дождливых дня.
A) 36 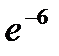 B) 18
B) 18 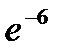 C) 9
C) 9 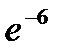 D) 12
D) 12 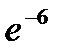 E) 6
E) 6 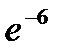
45.Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что в пути будет повреждено два изделия.
A) 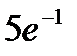 B)
B) 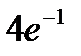 C)
C) 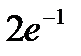 D)
D) 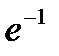 E)
E) 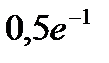
Случайных величин
1.Указать закон распределения, плотность вероятности которого определяется формулой 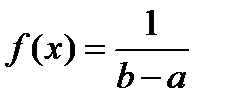 при
при 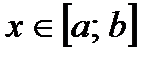 .
.
A) Равномерный B) Нормальный C) Показательный
D) Закон Пуассона E) Биномиальный
2.Указать закон распределения, функция распределения которого определяется формулой 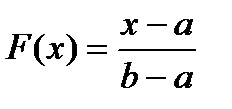 при
при 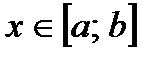 .
.
A) Равномерный B) Нормальный C) Показательный
D) Закон Пуассона E) Биномиальный
3.По какой формуле определяется математическое ожидание случайной величины Х, распределенной равномерно на отрезке 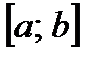 ?
?
A) 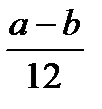 B)
B)