Если наклонные равны, то равны и их проекции.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Тест предназначен для студентов 1 курса.
Вопросы подобраны таким образом, чтобы можно было проверить подготовку студентов по усвоению соответствующих знаний и умений изученной дисциплины.
Предлагается пакет тестовых заданий по оценке качества подготовки студентов. Пакет содержит проверочные тесты, с помощью которых преподаватель может проверить качество усвоения пройденного материала:
- часть А – 80 заданий с кратким ответом – проверка теоретических знаний (задания закрытого типа);
- часть B – комплексный практический тест с 20-ю заданиями открытого типа;
- часть C – комплексный практический тест с 8-ю заданиями открытого развернутого типа.
Часть А (проверка теоретических знаний) - информационный тест, включающий в себя 20 заданий.
Часть А тестового задания включает в себя:
- выбор правильного ответа;
За каждый правильный ответ – 2 балла.
Максимальное количество баллов – 40.
Часть B (проверка практических знаний и умений) - комплексный практический тест, включающий в себя 8 заданий открытого типа со свободным ответом.
За каждый правильный ответ – 5 баллов.
Максимальное количество баллов – 40.
Часть C (проверка практических знаний и умений) - комплексный практический тест (письменное задание), включающий в себя 2 задания повышенного уровня сложности открытого типа с развернутым ответом.
За каждый правильный ответ – 10 баллов.
Максимальное количество баллов – 20.
ЧАСТЬ А
1. Даны векторы 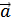 = (2; 3; -1),
= (2; 3; -1), 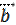 = (0; 1; 4). Найдите координаты вектора 2
= (0; 1; 4). Найдите координаты вектора 2 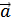 –
– 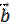 .
.
1) (4; 6; -2)
2) (4; 5; -6)
3) (2; 2; -5)
4) (2; 1; -9).
2. Плоскости α и β пересекаются по прямой a, прямая b лежит в плоскости α и пересекает плоскость β. Какого взаимное расположение прямых a и b?
Пересекаются
2) параллельны
3) Скрещиваются
4)Расположение прямых зависит от расположения плоскостей.
3. Плоскости α и β параллельны, через точку Aє a проведена прямая a, параллельная плоскости β. Прямая a…
1) Лежит в плоскости α
2) Пересекает плоскость α
3) Параллельная плоскости α
4) Может быть параллельной к плоскости α, а может пересекать ее.
4. Если две смежные стороны параллелограмма параллельны двум сторонам другого параллелограмма, то плоскости этих параллелограммов…
1) Совпадают
Параллельны
3)Совпадут или параллельны
4) Не могут иметь общих точек
5. Сколько плоскостей, перпендикулярных двум данным пересекающимисяплоскостям, можно провести через любую точку пространства?
1)Бесконечно много.
Невозможно
3)2
4)1
6. Плоскости квадратов ABCD и AB 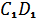 перпендикулярны AB = a. Найдите расстояние
перпендикулярны AB = a. Найдите расстояние 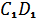 .
.
A
2) a 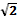 .
.
3) a 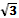
4)2a
7. Наклонная, проведенная из некоторой точки к плоскости α, вдвое длиннее ее проекции на плоскость. Чему равен угол между наклонной и плоскостью?
1) 30°
2) 45°
3) arctg 2
4) 60°
8. Найдите угловой коэффициент касательной к графику функции
f(x) = - 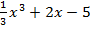 в точке с абсциссой
в точке с абсциссой 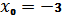
1) 11.
2) -7
3)-2
4)17,45
9. Найдите угловой коэффициент касательной к графику функции y=3sinx + 12x в точке 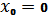
1) 1
2) 12
3) 15
4) 0
10. Найдите угловой коэффициент касательной к графику функции y = 10sinx + 22x в точке с абсциссой 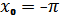
1) 20-15π
2) 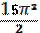
3) -5
4) 12
11. Выберете верные утверждения.
2) -4
3) 4
4) 1
17. Точка движется прямолинейно по закону S=60t-5t3. Через сколько времени после начала движения точка остановится.
1) 4с
2) 3с
3) 5с
С
18. Найти экстремум функции y=x2+4x+5
1) 0
2) 2
3) 1
4) 4
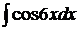 |
19. Вычислить интеграл
1) 6sin6x+c
2) 1/6 sin6x+c
3) –sin6x+c
4) 0
20. Вычислить производную в данной точке :y=3x-x5 в точке x0 = 1
1) 8
2) 0
3) 2
4) -2
21. Точка движется прямолинейно со скоростью υ(t)=9t2+t. Найти её ускорение через 2 секунды после начала движения.
1) 37 м/с2
2) 36 м/с2
3) 38 м/с2
4) 35 м/с2
22. Прямоугольник со сторонами 8 и 10 см вращается вокруг меньшей стороны. Найти площадь боковой поверхности тела вращения.
1) 80π
2) 160π
3) 100π
4) 2000π
23. Вычислить производную в данной точке (А): y=x/5-4 в точке x = 0
1) -4
2) 0,5
3) 0,2
4) 0
24. Вычислить производную в данной точке (А): y=3x3+4x2+2 в точке x = 0
1) 0
2) 2
3) 9
4) 17
25. Точка движется прямолинейно по закону S=3t3+t. Вычислить скорость точки через 3 секунды после начала движения
М/с
2) 84 м/с
3) 54 м/с
4) 80 м/с
26. Точка движется прямолинейно по закону S=3t4-4t3. Вычислить скорость точки через 2 секунды после начала движения
1) 36 м/с
М/с
3) 96 м/с
4) 72 м/с
27. Измерения прямоугольного параллелепипеда равны 15м, 9м и 25м. Найти ребро равновеликого ему куба.
1) 32 м
2) 30 м
М
4) 28 м.
28. 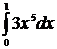 Вычислить определённый интеграл
Вычислить определённый интеграл
1) 0
2) 1
3) 0,5
4) 2
29. Найти площадь прямоугольного параллелепипеда по трём его измерениям: a=2 дм; b=6 дм; c=10 см.
1) 152 дм2
2) 10 дм2
3) 18 дм2
4) 184 дм2
30. Три латунных куба с рёбрами 3, 4 и 5 см переплавленны в один куб. Какое ребро у этого куба.
1) 7 см
2) 4 см
См
4) 5 см.
31. Вычислить производную в данной точке; y=cosx+sinx в точке x = 0
1) 1
2) 0
3) -1
4) π/2
32. Точка движется прямолинейно со скоростью υ(t)=2t3-3. Найти её ускорение через 3 секунды после начала движения.
1) 15 м/с2
2) 21 м/с2
3) 8 м/с2
4) 54 м/с2
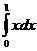 |
33. Вычислить определённый интеграл
1) 0
2) 1/2
3) 4
4) ¼
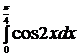 |
34. Вычислить определённый интеграл
1) 0
2) 1/2
3) -1/2
4) -1
35. Высота цилиндра на 10 см больше радиуса основания, а полная поверхность равна 144π см2. Найти радиус основания.
1) 14
2) 4
3) 10
4) 15
36. Как изменится объём цилиндра, если его радиус основания и высоту увеличить в 3 раза.
1) увелич в 81 раз
2) увелич в 3 раз;
3) увелич в 9 раз;
Увелич в 27 раз
37. 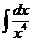 Вычислить интеграл
Вычислить интеграл
1) lnx4
2) 5/x5 + c
3) -1/3x3 + c
4) 1/4x3
38. Как изменится полная поверхность куба, если его ребро увеличить в 3 раза.
1) увелич в 6 раз;
2) увелич в 9 раз;
3) увелич в 27 раз;
4) увелич в 3 раза
39. Измерения прямоугольного параллелепипеда равны 15см, 9 см и 25 см. Найти ребро равновеликого ему куба(равного ему по объему):
1) 14 см
2) 49 см
См
4) 25 см.
40. Вычислить 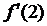 , если
, если 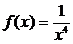 :
:
1) 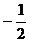 ;
;
2) 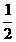 ;
;
3) 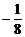 ;
;
4) 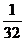 ;
;
41. Производная функции 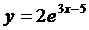 равна:
равна:
1) 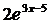 ;
;
2) 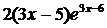 ;
;
3) 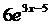 ;
;
4) 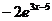 ;
;
42. Производная функции 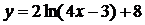 равна:
равна:
1) 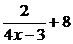 ;
;
2) 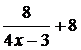 ;
;
3) 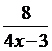 ;
;
4) 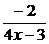 ;
;
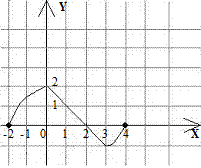
43. Укажите промежуток на котором производна функции 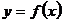 , заданной графиком, отрицательна
, заданной графиком, отрицательна
 1)
1) 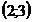 ;
;
2) 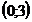 ;
;
3) 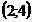 ;
;
4) 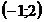 ;
;
44. Материальная точка движется прямолинейно и неравномерно по закону 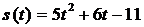 . Её мгновенная скорость через 2 сек после начала движения равна:
. Её мгновенная скорость через 2 сек после начала движения равна:
1) 26 м/c;
2) 15 м/c;
3) 21 м/c;
4) 16 м/с;
5) другой вариант ответа;
45. Вычислить 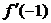 , если
, если 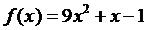
1) –18;
2) –17;
3) 7;
4) другой вариант ответа;
46. При каких значениях 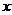 производная функции положительна?
производная функции положительна?
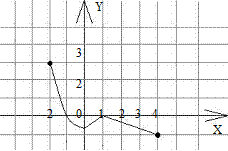 1)
1) 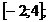
2) 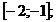
3) 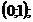
4) 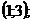
47. Вычислить 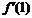 , если
, если 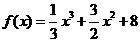 :
:
1) 12;
2) 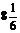 ;
;
3) 4;
4) другой вариант ответа.
48. Указать промежуток, в котором производная функции 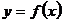 отрицательна.
отрицательна.
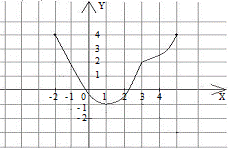 1)
1) 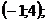
2) 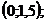
3) 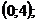
4) 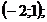
49. Скорость неравномерного прямолинейного движения материальной точки описывается формулой 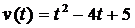 . Её ускорение в момент времени t= 4 сек равно:
. Её ускорение в момент времени t= 4 сек равно:
1) 5 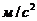 ;
;
2) 4 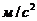 ;
;
3) 9 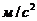 ;
;
4) другой вариант ответа.
50. Найти 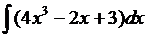
1) 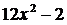 ;
;
2) 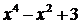 ;
;
3) 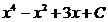 ;
;
4) другой вариант ответа.
51. Вычислить 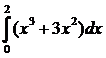
1) 24;
2)10;
3)12;
4) другой вариант ответа.
52. Скорость движения точки изменяется по закону 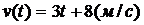 . Найти путь, пройденный точкой за 4 сек от начала движения:
. Найти путь, пройденный точкой за 4 сек от начала движения:
1)56 м;
2)20 м;
3)32 м;
4) другой вариант ответа.
53. Вычислить 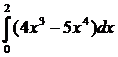
1) –48;
2)16;
3)-16;
4) другой вариант ответа;
54. Скорость движения точки изменяется по закону 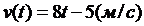 . Найти путь, пройденный точкой за 4 сек от начала движения.
. Найти путь, пройденный точкой за 4 сек от начала движения.
1)17 м;
2)84 м;
3) 44 м;
4) другой вариант ответа;
55. Найти 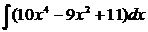
1) 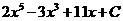 ;
;
2) 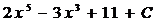 ;
;
3) 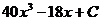 .
.
4) другой вариант ответа
56. Скорость движения точки изменяется по закону 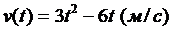 . Найти путь, пройденный точкой за 4 сек от начала движения:
. Найти путь, пройденный точкой за 4 сек от начала движения:
1) 112 м;
2)16 м;
3) 18 м;
4) другой вариант ответа.
57. Даны векторы 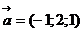
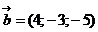 . Найти сумму
. Найти сумму 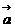 +
+ 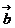
1) (5; -1; 4)
2) (3; 1; -4)
3) (3; -1; -4)
4) (3;-1; 4)
58. Найти скалярное произведение векторов 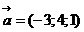 и
и 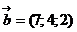
1) -5
2) -3
3) -7
4) 3
59. Найти угловой коэффициент касательной, проведенной к графику функцииy = 2x3 - 7x2 + 4x + 1 в точке с абсциссой х0 = -1
1) -12
2) 24
3) 25
4) 23
60. Материальная точка движется прямолинейно и неравномерно по закону 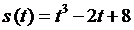 . Её мгновенная скорость через 3 сек после начала движения равна:
. Её мгновенная скорость через 3 сек после начала движения равна:
1) 25 м/c;
2) 33 м/c;
3) 29 м/c;
4) другой вариант ответа.
61. Поставьте в соответствие уравнению сферы его центр и радиус
a) 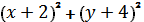 +
+ 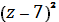 = 3 А) А (2; -4; 7) и R = 3.
= 3 А) А (2; -4; 7) и R = 3.
b) 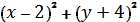 +
+ 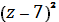 = 9 Б) А (-2; -4; 7) и R=
= 9 Б) А (-2; -4; 7) и R= 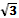 .
.
c) 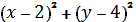 +
+ 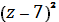 = 3 В) А (2; 4; 7) и R=
= 3 В) А (2; 4; 7) и R= 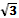 .
.
Варианты ответов:
1) a-А; b-А; c-В;
2) a-Б; b-А; c-В;
3) a-А; b-Б; c-В;
4) a-А; b-В; c-Б;
62. Установите соответствие
a)2πRH А) 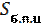
b)πRl Б) Sп.п.к
c) πR(l + R) В) 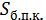
d) 2πR(H + R) Г) 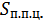
Варианты ответов:
1) a-А; b-Б; с-В; d-А;
2) a-Г; b-В; c-Г; d-Б;
3) a-Б; b-Б; c-Г; d-Г;
A-А; b-В; c-Б; d-Г.
63. Установите соответствие
a) πD А) 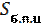
b) πR(l + R) Б) Sп.п.к.
c) 2πRH + 2π 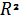 В)
В) 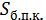
d)πDl Г) 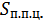
e)2πr
Варианты ответов:
1) a- А; b-Г; с-Б;d-В;
2) b-Г; c-Б; d-А; e-В;
3) b-Б; c-Г; d-В; e-А;
4) a-Г; b-Б; d-В; e-А.
64. Укажите возможное соответствие фигур и формул нахождения объемов.
 1)
1) 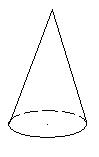 2) 3)
2) 3) 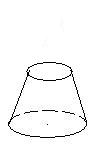 4)
4) 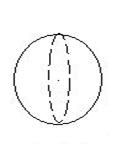
А) 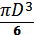 Б) πR(R + r) В)
Б) πR(R + r) В)  π
π 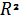 H Г)
H Г) 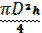
Варианты ответов
1) 1-Г; 2-Б; 3-В ; 4- А
В; 2- Г; 3- Б; 4-А
3) 1-А; 2-Б ;3-В; 4-Г
4) 1-Б ;2-А; 3-Г; 4-В.
65. В основании прямой призмы лежит равнобедренный треугольник со сторонами 4м, 4м и 2м, а диагональ меньшей по площади боковой грани - 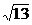 м. Найдите площадь боковой поверхности призмы.
м. Найдите площадь боковой поверхности призмы.
1) 60 м2
2) 30 м2
3) 48 м2
4) 96 м2
66. Боковое ребро правильной треугольной пирамиды равно 10м, а сторона основания – 12м. Найдите площадь боковой поверхности пирамиды.
1) 72 м2
2) 288 м2
3) 180 м2
4) 144 м2
67. Основание пирамиды – ромб со стороной равной 5м и диагональю 8м, а высота пирамиды равна меньшей диагонали основания. Найдите объем пирамиды.
1) 24 м3
2) 48 м3
3) 16 м3
4) 72 м3
68. Прямоугольник ABCD вращается вокруг стороны АВ. Найдите объем тела вращения, если ВС=3м, BD=5м.
1) 45p м3
2) 16p м3
3) 36p м3
4) 80p м3
69. Найдите объем конуса если его высота равна 6м, образующая 10м.
1) 128p м3
2) 64p м3
3) 640p м3
4) 256p м3
70. Наибольшее расстояние между двумя точками сферы равно 18м. Найдите площадь сферы.
1) 291p м2
2) 324p м2
3) 486p м2
4) 972 p м2
71. Наибольшее расстояние между двумя точками сферы равно 3 м. Найдите площадь сферы.
1) 13,5 м2
2) 72p м2
3) 36p м2
4) 9p м2
72. Сколько ребер, вершин и диагоналей у многогранника, имеющего наименьшее число граней.
1) Р-5; В-3; Д- 6;
2) Р-6; В-4; Д-0;
3) Р-6; В-4; Д-2;
4) Р-6; В-1; Д- 1;
73. Сколько вершин, ребер боковых ребер у призмы имеющей минимальное число граней.
1) В-6; Р -6; БР-3;
2) В-6; Р -9; БР-3;
3) В-6; Р -2; БР-5;
4) В-5; Р -4; БР-6;
74. Вычислите площадь, заштрихованную на рисунке.
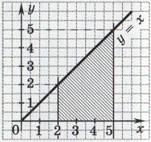
Варианты ответов:
1) 10,5
2) 11
3) 11,5
4)12,75
75. Вычислите площадь, заштрихованную на рисунке.
76.
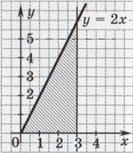
Варианты ответов:
1)8
2)9
3)10
4)11
77. Вычислите площадь, заштрихованную на рисунке.
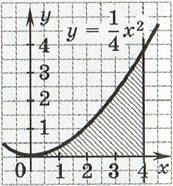
Варианты ответов:
1) 5/16
2) 64/12
3) 65/4
4) 1/6
78. В коробке находятся 2 белых, 3 черных и 4 красных шара. Наугад вынимается один шар. Найти вероятность того, что вынутый шар белый
1) 2/9
2) 3/9
3) 4/9
4) 2/7
79. В коробке находятся 2 белых, 3 черных и 4 красных шара. Наугад вынимается один шар. Найти вероятность того, что вынутый шар красный.
1) 2/9
2) 3/9
3) 2/7
4) 4/9
80. Элементы комбинаторики. Вычислить:
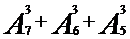
1) 382
2) 390
3) 290
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81. Вычислить:
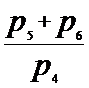
1) 7
2) 60
3) 35
ЧАСТЬ B
1. Напишите уравнение прямой, проходящей через начало координат, которая параллельна касательной к графику функции 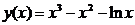 , проведенной в точке
, проведенной в точке 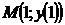 .
.
Отв 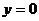
2. Напишите уравнение прямой, проходящей через начало координат, которая параллельна касательной к графику функции 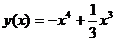 , проведенной в точке
, проведенной в точке 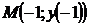 .
.
Отв 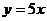
3. Напишите уравнение прямой, проходящей через начало координат, которая параллельна касательной к графику функции 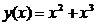 , проведенной в точке
, проведенной в точке 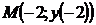 .
.
Отв 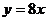
4. На графике функции 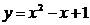 найдите точку М, в которой касательная к данному графику параллельна прямой
найдите точку М, в которой касательная к данному графику параллельна прямой 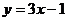 .
.
Отв 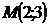
5. На графике функции 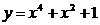 найдите точку М, в которой касательная к данному графику параллельна прямой
найдите точку М, в которой касательная к данному графику параллельна прямой 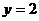 .
.
Отв 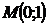
6. Угол между диагональю прямоугольного параллелепипеда и плоского основания равен 300. Найдите диагональ параллелепипеда, если стороны основания равны 2м и 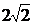 м.
м.
Отв4
7. Сторона основания правильной четырехугольной призмы равна 4м, а диагональ боковой грани – 5м. Найдите объем призмы
Отв48
1.
2.
3.
4.
5.
6.
7.
8. Сторона основания правильной четырехугольной призмы равна 5м, а диагональ боковой грани – 13м. Найдите объем призмы.
Отв300
9. Вычислите площадь фигуры, ограниченной линиями
y = 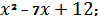 x=0; x=3; y = 0.
x=0; x=3; y = 0.
Отв 13,5
10. Вычислите площадь фигуры, ограниченной линиями
y = 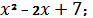 x = 0; x = 3; y= 0.
x = 0; x = 3; y= 0.
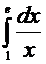 Отв 21
Отв 21
11. Вычислить определённый интеграл
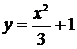 Отв 1
Отв 1
12. Найти площадь фигуры, заключённой между линиями: , осью ОХ и прямыми x=1 и x=5
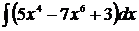 Отв 160/9
Отв 160/9
13. Вычислить интеграл
Отв 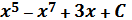
14. Найти площадь фигуры, ограниченной прямыми: y=4/x; x=1; x=e; y=0.
Отв 4
15. Площадь поверхности куба равна 96 дм2. Найти ребро куба (с точностью до 1 дм2).
Отв 4
16. Найти промежутки возрастания функции f(x) = x3 - 3x2 +1
Отв (- 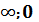 )
) 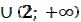
17. Найти минимум функции f(x) = 2x3 - 9x2 + 12x– 8
Отв -4
18. Найти промежутки выпуклости вверх графика функции y = x3 - 6x2 + 2x– 6
Отв (- 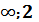 )
)
19. Найти точки перегиба графика функции y = x3 + 6x2 + 9x + 8
Отв (-2; 6)
20. Найти промежутки выпуклости вниз графика функции y = x3 -3x2
Отв (1; 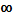 )
)
ЧАСТЬ С
1. Представьте число 3 в виде суммы двух положительных слагаемых так, чтобы сумма утроенного первого слагаемого и куба второго слагаемого была наименьшей.
2. Представьте число 5 в виде суммы двух положительных слагаемых так, чтобы произведение первого слагаемого и куба второго слагаемого было наибольшим.
3. Огораживают спортивную площадку прямоугольной формы площадью2500м2. Каковы должны быть ее размеры, чтобы на забор ушло наименьшее количество сетки «рабицы»?
4. Из шестиугольной призмы вырезали треугольную пирамиду, высота и площадь основания которой на 30 % и на 40% соответственно меньше высоты и площади основания призмы. Объем полученной пирамиды составляет от объема призмы
5.Исследовать и построить график функций y 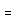 2x3
2x3 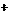 x2
x2  8x
8x 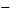 7
7
6.Исследовать и построить график функций 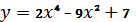
7.Решить уравнение: 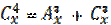
8.Вычислить площадь фигуры ограниченной графиками:
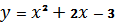
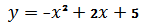
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Тест предназначен для студентов 1 курса.
Вопросы подобраны таким образом, чтобы можно было проверить подготовку студентов по усвоению соответствующих знаний и умений изученной дисциплины.
Предлагается пакет тестовых заданий по оценке качества подготовки студентов. Пакет содержит проверочные тесты, с помощью которых преподаватель может проверить качество усвоения пройденного материала:
- часть А – 80 заданий с кратким ответом – проверка теоретических знаний (задания закрытого типа);
- часть B – комплексный практический тест с 20-ю заданиями открытого типа;
- часть C – комплексный практический тест с 8-ю заданиями открытого развернутого типа.
Часть А (проверка теоретических знаний) - информационный тест, включающий в себя 20 заданий.
Часть А тестового задания включает в себя:
- выбор правильного ответа;
За каждый правильный ответ – 2 балла.
Максимальное количество баллов – 40.
Часть B (проверка практических знаний и умений) - комплексный практический тест, включающий в себя 8 заданий открытого типа со свободным ответом.
За каждый правильный ответ – 5 баллов.
Максимальное количество баллов – 40.
Часть C (проверка практических знаний и умений) - комплексный практический тест (письменное задание), включающий в себя 2 задания повышенного уровня сложности открытого типа с развернутым ответом.
За каждый правильный ответ – 10 баллов.
Максимальное количество баллов – 20.
ЧАСТЬ А
1. Даны векторы 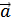 = (2; 3; -1),
= (2; 3; -1), 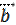 = (0; 1; 4). Найдите координаты вектора 2
= (0; 1; 4). Найдите координаты вектора 2 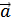 –
– 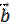 .
.
1) (4; 6; -2)
2) (4; 5; -6)
3) (2; 2; -5)
4) (2; 1; -9).
2. Плоскости α и β пересекаются по прямой a, прямая b лежит в плоскости α и пересекает плоскость β. Какого взаимное расположение прямых a и b?
Пересекаются
2) параллельны
3) Скрещиваются
4)Расположение прямых зависит от расположения плоскостей.
3. Плоскости α и β параллельны, через точку Aє a проведена прямая a, параллельная плоскости β. Прямая a…
1) Лежит в плоскости α
2) Пересекает плоскость α
3) Параллельная плоскости α
4) Может быть параллельной к плоскости α, а может пересекать ее.
4. Если две смежные стороны параллелограмма параллельны двум сторонам другого параллелограмма, то плоскости этих параллелограммов…
1) Совпадают
Параллельны
3)Совпадут или параллельны
4) Не могут иметь общих точек
5. Сколько плоскостей, перпендикулярных двум данным пересекающимисяплоскостям, можно провести через любую точку пространства?
1)Бесконечно много.
Невозможно
3)2
4)1
6. Плоскости квадратов ABCD и AB 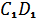 перпендикулярны AB = a. Найдите расстояние
перпендикулярны AB = a. Найдите расстояние 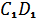 .
.
A
2) a 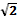 .
.
3) a 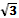
4)2a
7. Наклонная, проведенная из некоторой точки к плоскости α, вдвое длиннее ее проекции на плоскость. Чему равен угол между наклонной и плоскостью?
1) 30°
2) 45°
3) arctg 2
4) 60°
8. Найдите угловой коэффициент касательной к графику функции
f(x) = - 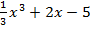 в точке с абсциссой
в точке с абсциссой 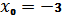
1) 11.
2) -7
3)-2
4)17,45
9. Найдите угловой коэффициент касательной к графику функции y=3sinx + 12x в точке 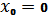
1) 1
2) 12
3) 15
4) 0
10. Найдите угловой коэффициент касательной к графику функции y = 10sinx + 22x в точке с абсциссой 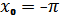
1) 20-15π
2) 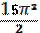
3) -5
4) 12
11. Выберете верные утверждения.
Если наклонные равны, то равны и их проекции.
2) Перпендикуляр длиннее наклонной.
12. Выберите верные утверждения.
1) Угол между параллельными прямой и плоскостью равен 90°.
