Первообразная. Неопределенный интеграл и его свойства.

Первообразная. Неопределенный интеграл и его свойства.

Первообразной для ф-цииf(x) на интервале [a;в] наз такая ф-цияF(x), для кот: F'(x)=f(x).

НИ от f(x) на [a;в] наз совокупность всех первообразных для f(x).

Св-ва НИ:

1) d(∫f(x)dx)=f(x)dx

2) ∫dF(x)= ∫ F'(x)dx=∫f(x)dx=F(x)+C

3) ∫Af(x)dx=A∫f(x)dx, A=const

4) ∫[f(x)+ϕ(x)]dx=∫f(x)dx+∫ ϕ(x)dx

Интегрирование по частям и замена переменной в неопределенном интеграле.

Инт-ие по частям: ∫d(u*v)= ∫udv+∫vdu= u*v=∫udv+∫vdu

∫udv=u*v-∫vdu

Правило выбора частей: -за ф-циюu(x) берем ту, кот существенно упрощается диф-ем

-за часть dv берем весь остаток

В некоторых случаях введением новой переменной (подстановкой или заменой) удается свести исходный интеграл к табличному или упростить. (t)

Комплексные числа. Их изображения на плоскости. Операции над комплексными числами.

Комплексным числом ƶназ число вида ƶ=x+iy, где х,у- действит числа; i-мнимая единица.

Арифметические действия над комплексными числами:

Сложение (х+уi)+(c+di)=(х+c)+(у+d)i

Вычитание (х+уi)-(c+di)=(х-c)+(у-d)i

Умножение ƶ_х* ƶ_с= (х+уi)-(c+di)

Многочлены. Корни многочлена. Разложение многочлена на множители.

Многочленом наз ф-ция вида у(х)=А₀х+А₁x^n-1+A₂x^n-2+…+A_n.

Число х₀наз корнем многочлена, если будучи подставлено в многочлен вместо х обращает его в тождество, т.е. Р_n(х₀)=0

Интегрирование дробно-рациональных функций.

Рац дробь: у= 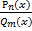; прав- n<m; неправ-n>m. Если дробь неправильная, то делением числителя на знаменатель получаем мнгч+ правильная рац дробь. Это действие иначе наз выделением целой части.

Интегрирование нескольких видов тригонометрических функций.

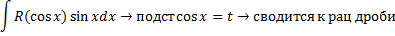
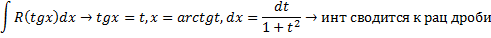
Интегрирование некоторых видов иррациональных выражений.Тригонометрические подстановки.

Иррациональности: 1) 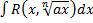→ подстановка ах+b=t

2)

3)

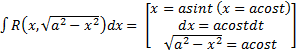
4)

5)

Тригонометрич. подстановки: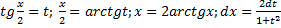

8. Дифференциальные уравнения первого порядка. Частное и общее решение. Задачи Коши. Формулировка теоремы существования и единственности решения задачи Коши.

Общий вид :F(x,y,y^’)=0 – неявная форма

y^’=f(x,y) явная ф-ма ДУ1

обязательный эл-т это y^’

Общим решением ДУ1 наз ф-ция у=ϕ(х,с), зависящая от произвольной постоянной с и удовлетворяющая 2-м условиям:

А) она является решением ДУ1 при любых значениях с;

В) каковы бы ни были нач условия х=х₀, у=у₀ всегда можно найти такое с, при котором полученное решение удовлетворяет этим условиям.

При конкретном значении с получим частное решение.

Теорема Коши: Пусть y^’=f(x,y)

Если f(x,y) и f^’_y(x,y) непрерывны в некобл-ти Dпл-ти f(x,y), то для любой т.М₀(х₀,у₀) сущ единое решение у(х) определенное в нек окрестности данной точки и удовлетворяющее условию у(х₀)=у₀

Отыскание этой ф-ции в данных условиях наз решением задачи Коши.

Теорема о структуре общего решения линейного однородного дифференциального уравнения 2-го порядка.

Если ф-ция у₁, у₂ образуют фундаментальную систему решений ЛОДУII, то общее решение этого ур-ния будет линейная комбинация у=С₁у₁+С₂у₂, с₁, с₂- const

Полный дифференциал.

Дифференциалом 1-го порядка ф-ции ƶ=f(x;y) наз главная линейная часть полного приращения ф-цииdz.

Dz складывается из двух частных дифференциалов.

Частный диф-л по х: z_x^’dx=d_xz

Метод наименьших квадратов.

Этот метод является одним из наиболее распространенных приемов статистической обработки экспериментальных данных, относящихся к различным функциональным зависимостям физических величин друг от друга. В том числе, он применим к линейной зависимости и позволяет получить достоверные оценки ее параметров a и b, а также оценить их погрешности.

31.Задача об объёме цилиндрического тела. Задача о массе плоской пластинки. Понятие двойного интеграла. Теорема существования.

Двойным инт-лом от ф-цииf(x,y)по обл Д из пл-ти ХОУ наз предел последовательности инт-х сумм, если он сущ и не зависит от способа разбиения олб Д на ∆S_i и от выбора т.М(х_i, y_i) в них.

Теорема сущ: Если обл Д с кусочно-гладкой границей Г ограничена и замкнута, ф-цияz=f(x,y) непрерывна в Д, то она инт-ма в обл Д, т.е. сущ число I=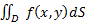

32. Свойства двойного интеграла. Вычисление двойного интеграла в прямоугольных координатах.

Св-ва: 1)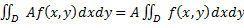

1) →

Первообразная. Неопределенный интеграл и его свойства.

Первообразной для ф-цииf(x) на интервале [a;в] наз такая ф-цияF(x), для кот: F'(x)=f(x).

НИ от f(x) на [a;в] наз совокупность всех первообразных для f(x).

Св-ва НИ:

1) d(∫f(x)dx)=f(x)dx

2) ∫dF(x)= ∫ F'(x)dx=∫f(x)dx=F(x)+C

3) ∫Af(x)dx=A∫f(x)dx, A=const

4) ∫[f(x)+ϕ(x)]dx=∫f(x)dx+∫ ϕ(x)dx